Көбейткіштерге жіктеу формулаларын қолдану

7.2020 цифрдан тұратын 1000 . . . 001 санының 1001 санына бөлінетінін дәлелдеңіз.

Шешуі.Берілген санды келесідей түрлендірейік:

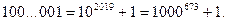
673 тақ сан болғандықтан берілген сан 1001 санына бөлінеді.

8. 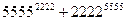қосындысының 7-ге бөлінетінін дәлелдеңіз.

Шешуі.Берілген қосындыны 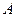арқылы белгілеп, оны келесі түрінде жазайық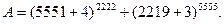

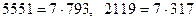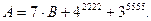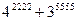Оң жақтағы әр жақшадағы қосындыны Ньютон биномы бойынша жіктесек онда, болатындықтан, әр жіктеудегі соңғы қосылғыштан басқа қосылғыштардың 7-ге бөлінетіндігін көреміз. Яғни, Енді қосындысының 7-ге бөлінетіндігін көрсетсек жеткілікті.

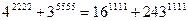болатындықтан, соңғы қосындының 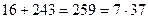санынына бөлінетіндігін көреміз. Сонымен, берілген сан 7-ге бөлінеді.

9.Кез келген натурал 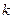үшін 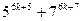қосындысының 9-ға бөлінетінін дәлелдеңіз.

Шешуі.Берілген қосындыны 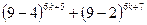түрінде жазайық.

Ньютон биномы бойынша жіктесек, онда 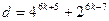қосындысы 9-ға қалдықсыз бөлінсе, онда берілген қосындының да 9-ға бөлінетінін көру қиын емес. 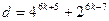қосындысын келесідей түрлендірейік:

.

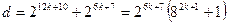Ал 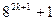қосындысы 9-ға бөлінетіндіктен, 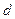қосындысы да 9-ға бөлінеді. Демек, берілген қосынды 9-ға бөлінеді.

10.Егер 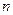тақ сан болса 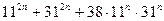қосындысының 40-қа бөлінетінін дәлелдеңіз.

Шешуі.Берілген қосындыны келесідей түрлендірейік:

.

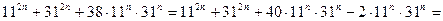
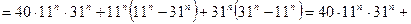
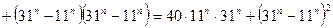Ал 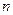тақ сан болғанда 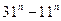айырымы 20-ға бөлінетінін ескерсек, онда бірінші және екінші қосылғыш 40-қа бөлінетіндіктен, олардың қосындысы да 40-қа бөлінеді.

11. 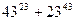қосындысының 66-ға бөлінетінін дәлелдеңіз.

Шешуі.Берілген қосындыны келесідей түрлендірейік:

.

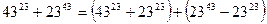Бірінші жақшадағы қосынды 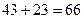санына бөлінетіндігі айқын. Екінші жақшадағы айырымды формула бойынша түрлендірсек, келесі өрнекті аламыз:

.

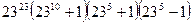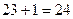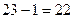Бұл көбейтіндінің және сандарына бөлінетіндігін көреміз. Сондықтан, ол 66-ға да бөлінеді.

12. 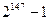санынын 343-ке бөлінетінін дәлелдеңіз.

Шешуі.Беріген айырымдыкөбейткіштерге жіктейік. Сонда,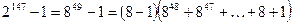болады. 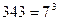болғандықтан, 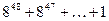қосындысының 49-ға бөлінетінін көрсетсек жеткілікті. Ол үшін әрбір 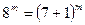қосылғышты Ньютон биномы формуласымен жіктейік. Сонда, әр жіктеудегі соңғы қосылғыш 1-ден өзге қосылғыштардың 7-ге бөлінетінін көреміз. Ал, 1-лердің саны 49 болғандықтан, 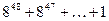қосындысы 49-ға бөлінеді.

Алдықпен бөлу

13. 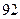-ге бөлінетін, ал 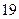-ға бөлгенде 3 қалдық қалатын ең кіші натурал

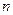санын анықтаңыз.

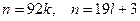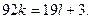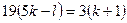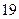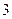Шешуі. десек, онда Бұл теңдікті түрінде жаза аламыз. және сандары өзара жай сандар болғандықтан

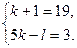
Осыдан, 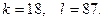Яғни, .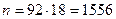

14. тақ сан және 3-ке бөлінеді. санын 6-ға бөлгендегі қалдықты анықтаңыз.

Шешуі.Есеп шарты бойынша 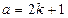және 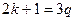. санын 6-ға бөлгендегі қалдық 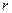болсын. Онда 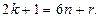Жоғарыдағы теңдіктерден 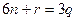болады. Осыдан 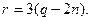Теңдіктің оң жағындағы өрнек 3-ке бөлінетіндіктен сол жағындағы өрнек те 3-ке бөлінуі керек. 6-ға бөлгендегі қалдық 1, 2, 3, 4, 5 болатындықтан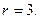

15. санын 3-ке бөлгендегі қалдық 1-ге, ал 4-ке бөлгендегі қалдық 3-ке тең. санын 6-ға және 12-ге бөлгендегі қалдықты анықтаңыз.

Шешуі. Есеп шарты бойынша 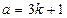және 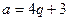. Онда 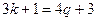немесе 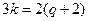. 2 мен 3 өзара жай сандар болғандықтан 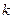жұп сан. 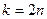болса, онда жоғарыдағы теңдіктерден 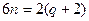немесе 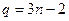болады. Онда 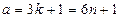және 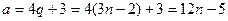немесе 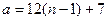. Демек, 6-ға бөлгенде 1 қалдық, ал 12-ге бөлгенде 7 қалдық қалады.

16. (3.29)

17.Цифрларының қосындысы5-ке бөлінетін 1-мен 1999 сандарының аралығында қанша бүтін сан бар?

Шешуі.Төрторынды сандарды 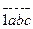түрінде өрнектейік. 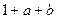қосындысын 5-ке бөлгендегі қалдық келесі сандардың бірі болуы мүмкін: 0, 1, 2, 3, 4. Осы қалдықтарға сәкес, 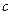-ны санның цифрларының қосындысы5-ке бөлінетіндей етіп анықтайық.

Қалдықтың мәні
с-ның мәні	0 немесе 5	4 немесе 9	3 немесе 8	2 немесе 7	1 немесе 6

Демек, әр қалдыққа қатысты, есеп шартын қанағаттандыратындай 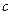-ның мәндері екеу.

1-мен 1999 сандарының аралығында бір таңбалы 5 саны ғана есеп шартын қанағаттандырады. Екі таңбалы сандарды 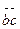деп белгілесек, мұндағы 1-ден 9-ға дейінгі тоғыз цифрлардың бірі. Яғни, цифрларының қосындысы5-ке бөлінетін екі орынды сандардың саны .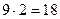

Үш орынды сандарды 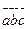деп белгілесек, мұндағы -ның қабылдайтын мәндері 1-ден 9-ға дейінгі тоғыз цифрлар болса, -ның қабылдайтын мәндері 0-ден 9-ға дейінгі он цифр. Яғни, үш орынды сандардың ішіндегі 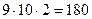сан есеп шартын қанағаттандырады. Осы сияқты, төрт орынды сандар 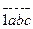болса, мен -ның әрқайсысының қабылдайтын мәндері 0-ден 9-ға дейінгі он цифр болатындықтан, 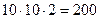төрт орынды санның цифрларының қосындысы5-ке бөлінеді.

Сонымен, 1-мен 1999 сандарының аралығында цифрларының қосындысы5-ке бөлінетін 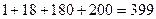сан бар.

Зара жай сандар

18. 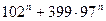өрнегінің 995-ке бөлінетінін дәлелдеңіз.

Шешуі. 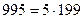және 5-пен 199 өзара жай сандар болғандықтан берілген өрнекгің 5-ке және 199-ға бөлінетінін көрсетсек жеткілікті. Ол үшін оны, жіктеу формулалары бойынша келесідей түрлендірейік: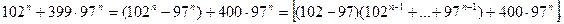

Оң жақтағы өрнектің 5-ке бөлінетінін көру қиын емес. Сондықтан берілген өрнек те 5-ке бөлінеді.

Енді берілген өрнекті басқаша түрлендірейік:

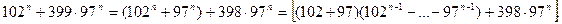
Оң жақтағы өрнек 199-ға бөлінеді. Демек, берілген қосынды өзара жай 5 және 199 сандарына бөлінетіндіктен, 995-ке бөлінеді.

19. Үш орынды екі санның арасындағы көбейту белгісі көрінбей қалып, орнына алты орынды сан жазылды. Нәтижесінде алғашқы көбейтіндіден үш есе үлкен сан жазылды. Сол санды табыңыз.

Шешуі.Үш орынды екі санның алғашқысы 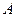, ал екіншісі 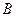болсын. Есеп шарты бойынша 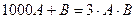. Бұл теңдіктен .

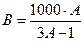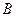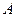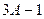бүтін сан болғандықтан, теңдіктің оң жағындағы бөлшектің мәні де бүтін сан болуы тиіс. және сандары өзара жай сандар болатындықтан, 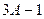саны 1000 санының бөлгіші болуы керек. 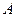үш орынды сан болғандықтан, 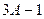саны үш немесе төрт орынды сан. 1000-ның ондай бөлгіштері екеу: 500 және 1000.

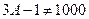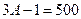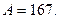, себебі 1001 саны 3-ке бөлінбейді. болса Онда 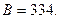Демек, жазылған алты орынды сан 167334.

20.Егер үш орынды санның бірінші цифрын 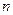-ге арттырсақ, ал екінші

және үшінші цифрларын 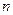-ге кемітсек, онда берілген саннан 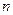есе үлкен сан аламыз. Берілген үш орынды санды және 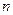-ді анықтаңыз.

Шешуі. 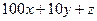берілген сан болсын. Есеп шарты бойынша

.

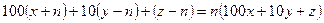Осыдан,

.

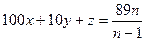89 жай сан болғандықтан не 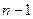саны 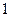-ге тең, немесе 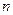саны 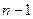санына бөлінеді. Екі жағдайда да 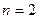болады. Демек, берілген сан 178.

21.(3.57)

22. (3.61)

Қарастырылған есептер әр деңгейдегі математикалық жарыстарда ұсынылған. Есептерді шығару барысында қарапайым жіктеу формулалары мен бүтін сандардың бөлінгіштік қасиеттеріне сүйендік. Ұсынылған есептерді басқа тәсілдермен де шығаруға болады.

Орытынды

Ғылыми-техникалық прогресс дәуірінде математика жаратылыстанудың, техниканың және өндірістің тілі мен кұралы ретінде пайданылады.

Оқыту - білім беру, ол оқушыны ғылыми білімнің жаңалықтарына ынталандыру. Бүгінгі жалпы білім беретін мектептердің мақсаттарының бірі әрбір шәкірттің жеке тұлға ретінде жалпы мәдениетін көтере отырып, жан-жақты дамуына мүмкіндік тудыру, оқушының өзіндік іс-әрекетін дамыту, оқу үрдісін ең тиімді тәсілмен ұйымдастыру.

Математиканы кәсіби меңгеруге даярлаумен қатар, таңдап алған мамандығына тәуелсіз, барлық оқушыларды белгілі бір деңгейдегі математикалық біліммен қаруландыру, оқытудың манызды мәселесі болып табылады.

Американдық педагог-математик Д.Пойа былай деген: "Математиканы білу деген не? Бұл - есептерді шығара білу, онда стандартты есептерді ғана емес ойлаудың еркіндігін, сананың сауаттығын, тапқырлықты керек ететін есептерді шығару". Сондықтан да, орта мектептегі математика курсының бірінші әрі ең басты міндеті есеп шығаруды меңгертуге тіреледі.

Математиканың теориялық негізін есеп түрінде меңгеру оқушылардың ойын белсендендіреді, икемділік, жүйелілік және тағы басқа қажетті қасиеттерді де қалыптастырады.

Математиканы үйренумен белсенді шұғылданудың негізі - есеп шығару болып табылады. Есеппен жұмыс істеуде мынадай үш кезеңді (Пойа бойынша) бөліп карауға болады:

1. Зерттеу кезеңі (әрекетпен кабылдауға жакынырақ және ен алдымен түсініктік немесе эвристикалық денгейде жүреді);

2. Қалыптасу кезеңі (терминологияны, анықтамаларды, теоремаларды дәлелдеумен байланысты неғұрлым жоғары деңгейге, ұғымдар деңгейіне көтеріледі);

3. Меңгеру кезеңі ең соңынан келеді, ол мәселенің «ішкі мәнін» табуға жауап береді. Оқытылған материал оқушылардың білім қорын молайтып, дүниетанымын кеңейтуі тиіс. Бұл кезең біріншіден, білімді жоғарырақ деңгейде жинақтауға жол ашады. Екіншіден, есеп шығару зерденің өзіндік ерекшелігіне жатады, ал зерде адамнын ерекше касиеті. Сондықтан да есеп шығару адамның ақыл ой әрекетінің ең манызды көрінісінің бірі ретінде қарастырылады.

Оқушыларды есептерді шығаруға үйрету бойынша жүргізілетін жұмыстарды талдау, есеп шығарып отырған оқушыларды бақылау, есептерді шығару кезінде оқушылардың алдында тұрған қиындықтарын арнайы зерделеу осындай шеберлікке мыналарды жатқызуға болады:

1. Берілген есептің құрамын (оның құрамдас бөліктерін) талдай білу;

2. Құрамдас бөліктері арасындағы байланысты бөліп көрсете алу;

3. Айқындалған құрылымды есепті шешу үшін пайдалана алу;

4. Типті есептерді шығарудың үйреншікті алгоритмдерін іске асыра алу;

5. Таңдап алынған алгоритмді іске асырудан уақытында бас тарта алу немесе іске асыру кезінде жіберілген қателіктерді табу;

6. Есептерді шығару тәсілдерін бір жүйеге келтіре алу;

Аталған шеберлікті қалыптастыру үшін (тікелей сабақ кезінде) оқыту міндеттерінің жүйесін таңдау қажет. Бұл жағдайда мынадай талаптар сақталуы керек деп есептейміз:

Жұмыстың келешекке қарай нақты жоспардануы, тапсырмалар сабақ кезінде оқытылатын тақырыпқа сәйкес келуі қажет.

Негізгі мақсаты келесі шеберлік топтарын құрастыру болып табылатын тапсырмалар көзделуі тиіс:

Тақырыпқа қатысты кез келген қарапайым есепті шығара алу шеберлігін қалыптастыратын тапсырмалар.

Жекелеген тәсілдерді пайдалану мүмкіндігін жүзеге асыра алу, оларды іске асыру, жүйеге келтіру, қолдану шеберлігін қалыптастыратын тапсырмалар.

Есеп шешімдерін тексеруге, өз бетімен типтік есеп құрастыруға арналған тапсырмалар.

Есепті шешуді қиындату немесе жеңілдету шеберлігін қалыптастыруға арналған тапсырмалар.

Санның бүтін бөлігіне қатысты есептер шығару барында оқушылар математикалық жаңа білімдерді игеріп, практикалық іс-әрекетке дайындалады. Мұндай есептер олардың логикалык ойлау қабілетін дамытуға үлкен әсер етеді. Санның бүтін және бөлшек бөлігі бар есептердің ішінде қалыпты емес ойлауды талап ететін есептер жиі кездеседі. Ондай есептерді тек жақсы оқитын оқушыларға ғана емес, барлық оқушыларға ұсыну керек. Әсіресе логикалық ойлау қабілеті төмен оқушыларға мұндай есептер өте қажет.

Мұндай eсептер шығару барысында оқушыларға көптеген алғашқы математакалық ұғымдар қалыптастырыльп, бастапқы ережелер мен қағидаларға түсініктер беріледі. Мысалы, сандарға қолданылатын арифметикалық амалдардың қасиеттерін, шамалардың айырмасы мен қатынастары және т. б. Осы сияқты мәселелер туралы түсініктер практикалық есептер арқылы меңгеріледі.

Қандай да болмасын есеп белгілі бір құбылыстың, процестің, жағдайдың сөз арқылы сипатталуы болып табылады. Есептегі кездесетін шамалар өзара тығыз байланыста болып келеді.

2014 жылдың ақпан-сәуір айы аралығында өндірістік практика кезінде №54 мектеп – лицейінде математиканы тереңдетіліп оқытылатын 10 «ә» сыныбында сабақ жүргіздім. Осы сыныпта «Бөлінгіштік және оның қасиеттері» тақырыбы бойынша сәуірдің 4-і күні факультативті сабақ өткіздім. Сабақ барысында санның бүтін бөлігінің анықтамасы және бірнеше қасиеттері айтылып және оларға мысалдар көрсетілді. Бірнеше жаттығу есептері шығартылды. Сабаққа математика пәнінің екі мұғалімі, сынып жетекшісі және физика пәнінің мұғалімі қатысты. Сабақты қатысушылар оқушылардың тақырыпты дұрыс меңгеріп, сабақта белсенді жұмыс істегендігін атап өтіп, жоғары бағалады.

7 – сәуір күні осы сыныпта тақырып бойынша бақылау жұмысын жүргіздім. Бақылау жұмысы 2 нұсқада, ал әр нұсқада 3 есептен болды. Бұл бақылау жұмысына барлығы 25 оқушы қатысты. Бақылау нәтижесі келесідей болды: 6 оқушы «5», 9 оқушы «4» және қалған 10 оқушы «3» деген баға алды.

Санның бүтін және бөлшек бөлігі бар есептерді шығаруды таным процесі ретінде қарастыруға болады, өйткені оқушы есеп шығару нәтижесінде өзіне бұрын белгісіз болып келген материалдармен, практикада қолдану тәсілдерімен танысады. Соның негізінде осындай есептер, оқу процесінде дүние танудағы математиканың алар орынын оқушыларға түсіндіруге, өмір мен өндіріске математиканы қолдануды үйретуге жағдай жасайды. Санның бүтін және бөлшек бөлігі бар есептер шығару арқылы оқушылардың ізденушілігі, танымдық іс-әрекеттері, іскерлігі, есеп шығару мәдениетті өседі. Бұл тақырыптағы есептер оқушылардан оқылған материалдың жалпы мазмұнын білумен қатар, оларды пайдалана отырып, кейбір практикалық мәселелерді шеше білуге үйретеді.

Орта оқу орындарында математиканы оқытудың мақсаты: оқушылраға күнделікті өмірде және қазіргі қоғамда пайдалы еңбек еткенде қажет болатын және де басқа пәндерді оқып үйренуге, білімін ары қарай жалғастыруға толық мүмкіншілік беретін математикалық білім, іскерлік және дағдылардың негізін берік және саналы түрде меңгеруін қамтамасыз ету.

Орта білім беретін мектептерде әрбір шәріктті жеке тұлға деп санап, оларды өз сұраныстарына, мүдделеріне сай оқыту мен тәрбиелеудің сан қилы үлгілерін қолдану көзделген. Бұл жағдайда оқыту технологиясын өзгертуді, оқушылардың өз бетінше білім алуға, өзін-өзі дамытуға, ұйымдастыруға үйрету мәселелеріне көп көңіл бөлу қажет.

Ғылым мен өндірістің дамуына математиканың қажеттілгі, математикалық білімнің қолданылу аясының кеңейуі еліміздегі әрбір оқушының математикалық білімнің толық болуының мәнін және маңызын күшейте түседі. Бұл еліміздің әрбір азаматына орта білім алуға міндет арта отырып, мұғалім қауымынан, оқушылардың математикалық дайындығының сапасын көтеруді және білімінің қандай да бір деңгейіне кепілдік беруін қамтамасыз етуді талап етеді.

Жалпы білім берудің негізгі мәселелерінің бірі – терең білім алу процесі мен оқушылардың ойлау қабілетін, оқуға деген ынтасын дамыту процесін біріктіру болып табылады деген қорытынды жасауға болады.

Нұсқа

1.Кез келген натурал 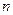үшін 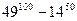санының 5-ке бөлінетінін дәлелдеңіз.

2. 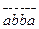санының 11-ге бөлінетінін дәлелдеңіз.

3. Егер екі орынды санды цифрының қосындысына бөлсе, онда бөлінді 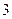, ал қалдық 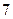болады. Осы санды табыңыз.

Нұсқа

5. Кез келген натурал 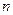үшін 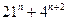санының 17-ге бөлінетінін дәлелдеңіз.

6. 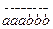санының 37-ге бөлінетінін дәлелдеңіз.

Егер екі орынды санды цифрының қосындысына бөлсе, онда бөлінді 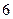, ал қалдық 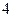болады. Осы санды табыңыз.

Нұсқа

5. Кез келген натурал 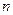үшін 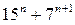санының 8-ге бөлінетінін дәлелдеңіз.

6. 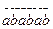санының 7-ге бөлінетінін дәлелдеңіз.

Егер екі орынды санды цифрының қосындысына бөлсе, онда бөлінді 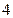, ал қалдық 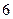болады. Осы санды табыңыз.

Нұсқа

4. Кез келген натурал 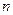үшін 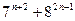санының 57-ге бөлінетінін дәлелдеңіз.

5. 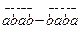санының 9-ға және 101-ге бөлінетінін дәлелдеңіз.

Егер екі орынды санды цифрының қосындысына бөлсе, онда бөлінді 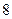, ал қалдық 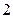болады. Осы санды табыңыз.