Ошибки репрезентативности (представительности)

Малая выборочная совокупность

Малая выборочная совокупность – это совокупность (выборка), объемом до 30 вариант.

Данные малой выборочной совокупности обрабатываются без предварительной группировки всех единиц совокупности.

Далее приводится полная характеристика изучаемого объекта.

Например:

Изучаемый объект – сосновый древостой

Изучаемый признак – диаметр дерева на высоте 1,3 м

Способ формирования выборочной совокупности - случайный

Объём совокупности – 30 деревьев

Данные обмера диаметров сосны на высоте 1,3 м приведены в таблице 1.1.

Таблица 1.1 – Экспериментальные данные исследуемого объекта (соснового древостоя)

	I	II	III	IV	V
	36,50	29,00	27,50	37,00	36,00
	28,00	27,00	24,00	38,00	37,00
	37,00	27,00	27,00	35,00	28,00
	28,50	22,00	34,00	36,00	24,00
	33,50	30,50	36,00	30,00	26,00
	31,00	34,00	28,00	32,00	33,00

Расчет статистических показателей для малой выборочной

Совокупности

Средняя величина(арифметическая) – наиболее представительная характеристика распределения, это центр распределения изучаемого признака:

,

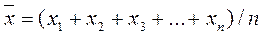где x₁ , x₂ , x₃ , x_n – каждое значение варианты совокупности; n – объем выборочной совокупности.

Например: 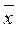=(36,50+29,00+27,50+37,00+36,00+…+33,00)/30 =31,08 см

Сумма квадратов отклонений (СКО) – сумма отклонений каждой варианты от средней величины (от центра распределения совокупности):

,

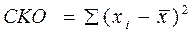где x_i – каждое значение варианты совокупности; 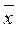– средняя величина.

Например:

СКО = (36,50-31,08)²+(29,00-31,08)²+ (27,50-31,08) ² +(37,00-31,08)²+(36,00-31,08)²+…+(33,00-31,08)²=632,04 см ²

Дисперсия – это средний квадрат отклонений всех вариант совокупности от средней величины. Дисперсия характеризует степень разнообразия (изменчивости) объекта:

.

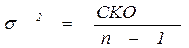Например: 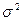= 632,04 / (30-1) = 21,79 см ².

Стандартное отклонение (среднее квадратическое отклонение) – основной показатель вариации, характеризующий варьирование значений признака вокруг центра распределения. Среднее квадратичное отклонение является мерой надёжности средней величины. Чем меньше его численное значение, тем лучше средняя арифметическая отражает собой всю статистическую совокупность.

.

Например: 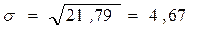, см

Коэффициент вариации– показатель меры изменчивости изучаемого признака (среднее квадратическое отклонение), выражающий ее в относительных единицах (то есть в процентах). Он представляет собой средний процент отклонения вариант от их среднего значения. Коэффициент вариацииявляется наиболее распространенным показателем, используемым для оценки типичности средних величин. Данная характеристика не зависит от принятых единиц измерения, и поэтому может применяться для сравнительной оценки величины варьирования различных признаков, как в пределах одной совокупности, так и в разных совокупностях. Вместе с тем он в значительной степени зависит от средней величины, и поэтому его применяют ограниченно случаями, когда имеет место естественное (от нуля) начало отсчета или сходные начала отсчета:

%.

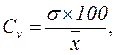Например: C_v = 4,67×100 = 15,03 %

31,08

По величине расчётного коэффициента вариации определяется уровень изменчивости признака с помощью шкалы Мамаева представленной в таблице 1.2.

Таблица 1.2 Шкала Мамаева для установления уровня изменчивости признака

Величина коэффициента вариации, %	Уровень изменчивости
до 7	очень низкий
7 – 15	низкий
16 – 25	средний
26 – 35	повышенный
36 – 50	высокий
более 50	очень высокий

Например: Расчётный коэффициент вариации С_v = 15,03 % тогда уровень изменчивости диаметра дерева на высоте 1,3 м низкий, т. к. коэффициент вариации находится в пределах от 7 до 15 %.

Коэффициент дифференциации – характеризует изменчивость признака, выражая ее в относительных единицах. Смысл данного показателя такой же, как и у коэффициента вариации, но он устраняет его ограничения:

,

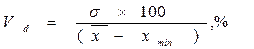где x_min – минимальное значение варианты изучаемого признака в совокупности.

Степень дифференциации признака определяется по величине коэффициента дифференциации с помощью таблицы 1.3.

Таблица 1.3 Классификация степени дифференциации признака

Величина коэффициента дифференциации, %	Степень дифференциации
до 13	слабая
13 – 27	умеренная
28 – 38	средняя
39 – 53	значительная
54 – 70	большая
более 70	очень большая

Например: V_d = 4,67×100 =51,43 %

(31,08 – 22,00)

Степень дифференциации значительная, т. к. коэффициент дифференциации находится в пределах от 54 до 70 %.

Ошибки репрезентативности (представительности)

В результате изменчивости (варьирования) изучаемого признака, между статистическими показателями выборочной совокупности и генеральной, могут наблюдаться некоторые расхождения, которые являются случайными ошибками выборки и называют основными ошибками репрезентативности того или иного статистического показателя.

Ошибка средней величины:

.

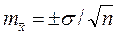Например: .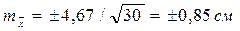

Ошибка стандартного отклонения:

.

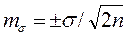Например: .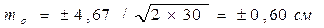

Ошибка коэффициента вариации:

.

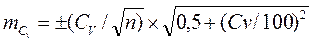Например: .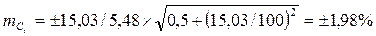

Ошибка точности:

.

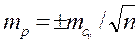Например: .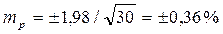

Точность опыта

(относительная ошибка опыта)

Показатель точности опыта выражает величину ошибки средней величины в процентах от самой средней. Точность опыта или процент ошибки наблюдения – это процент расхождения между генеральной и выборочной средней.

Чем меньше показатель процента ошибки, тем точность опыта выше.

Точность опыта считается удовлетворительной, если численное значение данного показателя не превышает 5 %. Если показатель точности больше 5 % , то рекомендуется увеличить число наблюдений или число повторностей. Точность опыта можно повысить (численное значение соответственно снизить) путём повышения точности измерений объектов опыта.

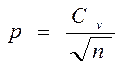или .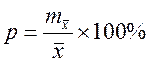

Например: 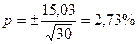.
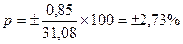