Текст програми
program gauss(input,output);
{розв'язування системи рiвнянь методом гауса'}
TYPE
dvmr = array[0..10,0..10] of real;
ovmr = array[0..10] of real;
var i,j,n,m:integer;
n1,m1,l1:integer;
aa,a,p,g:dvmr;
x,y,riz:ovmr;
b,ii:integer;
ab:real;
fr:text;
Procedure GELG(A:dvmr; Var B:ovmr; n:integer);
Var i,j,k,l : integer;
r : real;
Begin
{ ************************************************}
{ Пiдпрограма розв`язування системи лiнiйних }
{ алгебраїчних рiвнянь методом Гауса }
{ з вибором головного елемента }
l:=0;
for i:=1 to N do begin
k:=i; r:=Abs(A[i,i]);
for j:=i+1 to N do
if Abs(A[j,i])>r then begin
k:=j; r:=Abs(A[j,i]);
end;
if r<>0 then begin
if k<>i then begin
r:=B[k]; B[k]:=B[i]; B[i]:=r;
for j:=i to N do begin
r:=A[k,j];
A[k,j]:=A[i,j];
A[i,j]:=r;
end;
end;
r:=A[i,i]; B[i]:=B[i]/r;
for j:=i to N do A[i,j]:=A[i,j]/r;
for k:=i+1 to N do begin
r:=A[k,i]; B[k]:=B[k]-r*B[i];
for j:=i to N do A[k,j]:=A[k,j]-r*A[i,j];
end;
end
else begin l:=1; i:=N+1; end;
end;
if l<>1 then begin
for i:=N-1 downto 1 do begin
for j:=i+1 to N do B[i]:=B[i]-A[i,j]*B[j];
end;
end;
End;
{процедура вводу матрицi }
procedure vvidmat(var a:dvmr;n,m:integer);
var i,j:integer;
begin
for i:=1 to n do
for j:=1 to m do
readln(a[i,j]);
end;
{процедура вводу вектора }
procedure vvidvek(var x:ovmr;n:integer);
var i:integer;
begin
for i:=1 to n do
readln(x[i]);
end;
{процедура виводу матрицi на друк}
procedure drukmat(a:dvmr;n,m:integer);
var i,j:integer;
begin
for i:=1 to n do
begin
for j:=1 to m do
write(fr,a[i,j]:5:2,' ');
writeln(fr);
end;
end;
procedure drukvek(x:ovmr;n:integer);
var i:integer;
begin
for i:=1 to n do
writeln(fr,x[i]:5:3);
end;
begin
assign(fr,'gres.txt');
rewrite(fr);
{побудова матрицi системи}
writeln('введiть порядок системи');
readln(m);
writeln('ввiд с-ми');
vvidmat(aa,m,m);
writeln('ввiд вiльних членiв');
vvidvek(x,m);
rivvek(x,y,m);
writeln(fr,'матриця системи');
drukmat(aa,m,m);
writeln(fr,'вiльнi члени');
drukvek(x,m);
gelg(aa,x,m);
{знаходження i друк розв"язкiв}
writeln(fr,'розв"язок');
drukvek(x,m);
{знаходження нев'язок}
writeln(fr,'нев"язки');
for i:=1 to m do
begin
riz[i]:=0;
for j:=1 to m do
riz[i]:=riz[i]+aa[i,j]*x[j];
riz[i]:=riz[i]-y[i];
writeln(fr,'riz[',i:1,']=',riz[i]:2:2);
end;
close(fr);
end.
Результат роботи програми
Матриця системи
2.00 1.00 1.00
4.00 3.00 2.00
1.00 4.00 5.00
Вiльнi члени
2.00
2.00
1.00
розв"язок
1.222
-2.000
1.556
нев"язки
riz[1]=0.00
riz[2]=0.00
riz[3]=0.00
Розв’язок системи рівнянь за допомогою пакету MathCad
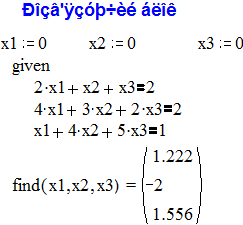
Знаходження визначника матриці методом Гауса
В результаті перетворень Гауса система (або матриця) зводиться до форми, яка дає змогу легко обчислити визначник матриці.
Представлена програма на мові Pascal (версія TurboPascal6 і вище) здійснює перетворення матриці за схемою Гауса та знаходження визначника. Для контролю визначник тієї ж матриці обчислено за допомогою пакету MathCad. Результати співпадають.
