Моделирование системы и анализ полученных результатов
ПРИМЕР 2.2а (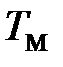 
> 
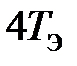). Провести моделирование нескорректированного замкнутого контура скорости с двигателем типа 2ПБ132МУХЛ4. Оценить качество переходных процессов. Определить установившиеся ошибки относительно задающего воздействия и момента сопротивления. Значения параметров принимаем по примерам 1.1а, 1.2а, 1.3а: 
В; 
= 11; 
; R = 0,9 Ом; i = 69; 
η =0,92; 
; 
; 
; 
; 
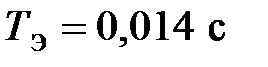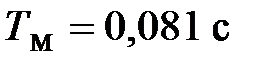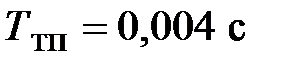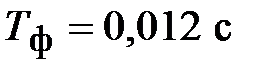Н·м.
Решение.Проведем моделирование замкнутого по скорости электропривода в соответствии со схемой, показанной на рисунке 2.1.
ССДМ ЭП в среде MatLab представлена на рис. 2.15. В блоке Step вводится значение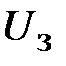 
=10 В.
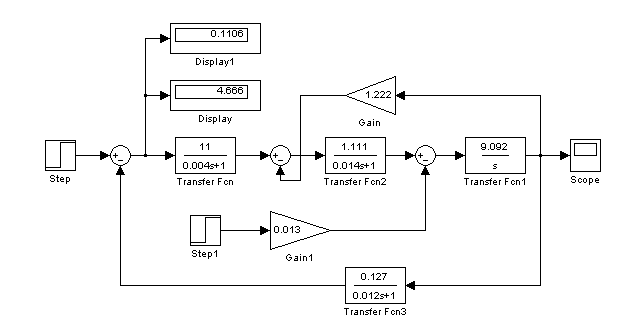
Рис. 2.15. ССДМ нескорректированного контура скорости
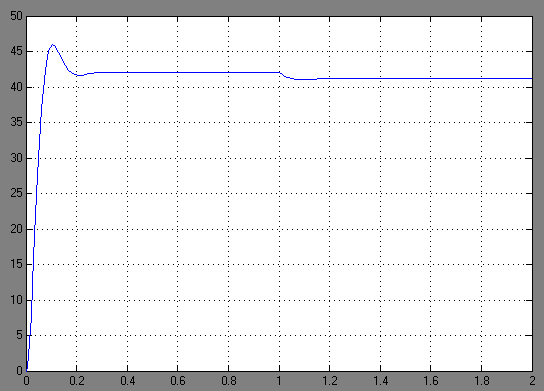
На рис. 2.16 представлена зависимость угловой скорости от времени нескорректированного контура скорости. Наброс момента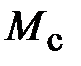 
производился через 1 с после пуска системы «преобразователь – двигатель».
Из графика видно, что установившееся значение скорости двигателя без нагрузки составляет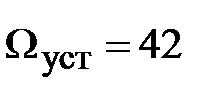 
рад/с. За счет влияния 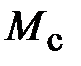угловая скорость уменьшилась примерно на 1 рад/c.
, рад/с
t, c
Рис. 2.16. Зависимость угловой скорости от времени нескорректированного контура скорости
График характеризует колебательную систему с числом колебаний N= 1 и перерегулированием около 9 %. Время протекания переходного процесса составляет 0,3 с. Наличие колебаний обусловлено комплексно-сопряженными корнями характеристического уравнения замкнутой системы.
На рисунке 2.15 в блоках Displayпоказаны установившиеся ошибки по задающему воздействию (Display) и по моменту сопротивления (Display1), которые составили соответственно
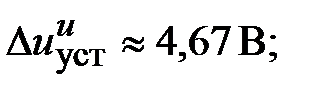
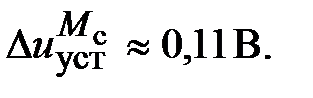
Таким образом, суммарная установившаяся ошибка электропривода с двигателем типа 2ПБ132МУХЛ4
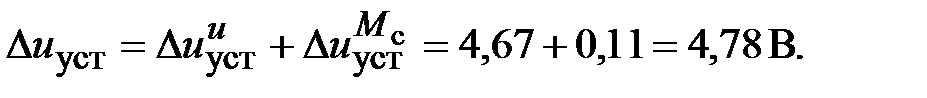
Результаты моделирования подтверждают правильность расчетов, проведенных в примере 2.1а.
ПРИМЕР 2.2б ( 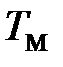< 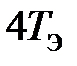). Провести моделирование нескорректированного контура скорости с двигателем типа 2ПБ90МУХЛ4. Оценить качество переходных процессов. Определить установившиеся ошибки относительно задающего воздействия и момента сопротивления. Значения параметров принимаем по примерам 1.1а, 1.2а, 1.3а: В; = 22; 
; 
; R = 19 Ом; i = 882; η =0,8; 
; 
; 
; ; 
; 
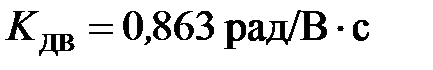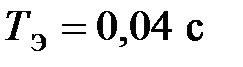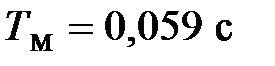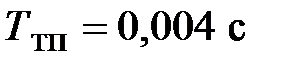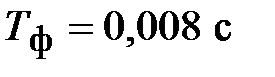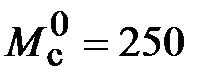Н·м.
Решение.Суммарная индуктивность якорной цепи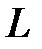 
с учетом индуктивности сглаживающего дросселя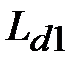 
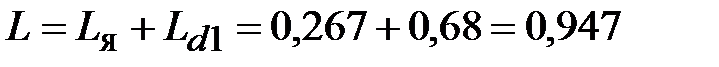Гн.
Тогда электромагнитная постоянная времени
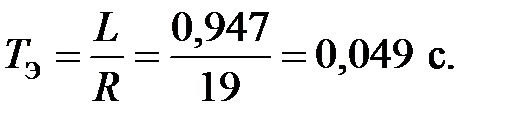
ССДМ ЭП в среде MatLab представлена на рис. 2.17. В блоке Step вводится значение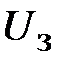 
=10 В.
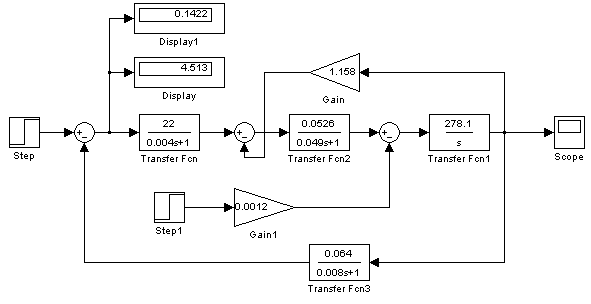
Рис. 2.17. ССДМ нескорректированного
контура скорости
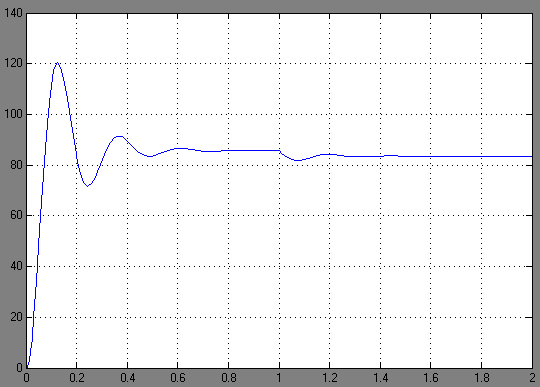
На рис. 2.18 показана зависимость угловой скорости вращения от времени нескорректированного контура скорости. Наброс момента 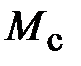статической нагрузки производился также через 1 с после пуска системы «преобразователь – двигатель».
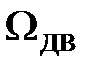, рад/с
t, c
Рис. 2.18. Зависимость угловой скорости от времени нескорректированного контура скорости
Как видно из графика, переходный процесс является колебательным с числом колебаний N= 2 и перерегулированием около 40 %. Время протекания переходного процесса составляет 0,7 с.
Установившееся значение скорости двигателя без нагрузки составляет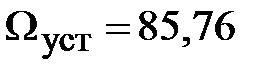 
рад/с. Наброс нагрузки обусловливает некоторое уменьшение установившегося значения скорости вращения.
Установившиеся ошибки относительно задающего воздействия и момента сопротивления при моделировании нескорректированного контура скорости составили соответственно
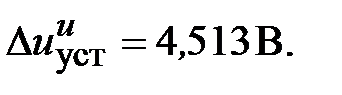
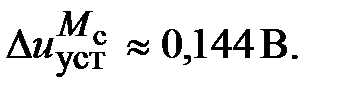
Таким образом, суммарная установившаяся ошибка электропривода с двигателем типа 2ПБ90МУХЛ4
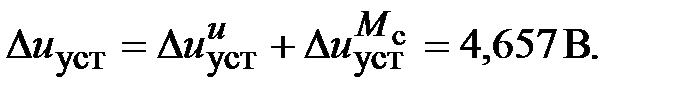
Результаты моделирования подтверждают правильность расчетов, проведенных в примере 2.1б.
Очевидно, что процессы в замкнутом контуре скорости необходимо оптимизировать за счет применения ПИД-регулятора, обеспечивающего увеличение точности благодаря интегральной составляющей и уменьшение колебаний благодаря дифференциальной составляющей.
Отчётные материалы
1. Расчет установившихся ошибок.
2. ССДМ нескорректированного контура скорости, характеристика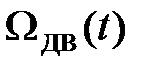 
, определение установившихся ошибок.
Контрольные вопросы
1. Сформулировать теорему о конечном значении.
2. Записать передаточную функцию замкнутой системы.
3. Записать передаточную функцию замкнутой системы относительно ошибки по задающему воздействию.
4. Записать передаточную функцию замкнутой системы относительно ошибки по возмущающему воздействию.
5. Начертить структурную схему динамической модели контура скорости.
6. Вывести формулу для расчета установившейся ошибки относительно задающего воздействия.
7. Вывести формулу для расчета установившейся ошибки относительно возмущающего воздействия.
8. Пояснить порядок моделирования ССДМ нескорректированного контура скорости в MatLab Simulink.
ЛАБОРАТОРНАЯ РАБОТА № 3