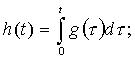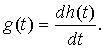Дифференциальное уравнение
Дифференциальное уравнение имеет следующий вид:
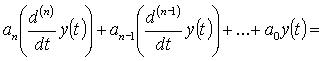
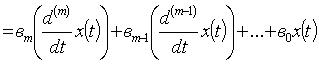 ,
,
где 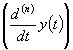 – обозначение производной n-ного порядка.
– обозначение производной n-ного порядка.
При переходе в статический режим 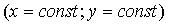 получаем
получаем
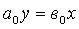 или
или 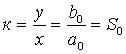 ,
,
где S0 – чувствительность, к – статический коэффициент преобразования.
Иначе дифференциальное уравнение может быть представлено в виде:
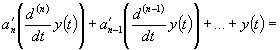
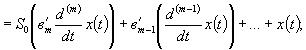
где:
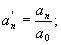
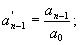

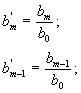
и так далее.
Порядок дифференциального уравнения определяется числом n. Наиболее часто встречаются дифференциальные уравнения первого (n=1) и второго (n=2) порядков.
1.12.2 Передаточная функция
Передаточная функция- отношение преобразования Лапласа выходной величины СИТ к преобразованию Лапласа входной величины при нулевых начальных условиях.
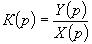 ,
,
где 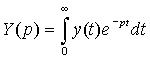 – преобразование Лапласа выходной величины у(t),
– преобразование Лапласа выходной величины у(t), 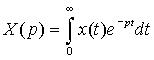 – преобразование Лапласа входной величины x(t).
– преобразование Лапласа входной величины x(t).
Передаточную функцию получают с помощью преобразования дифференциального уравнения
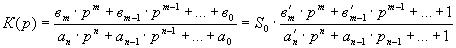
Для сравнения динамических свойств СИТ используют приведенную передаточную функцию (передаточную функцию К(р), отнесенную к статическому коэффициенту преобразования)
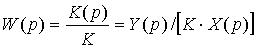 .
.
Амплитудно-фазовая характеристика
Амплитудно-фазовая характеристика (АФХ) СИТ 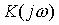 (комплексный коэффициент преобразования (передача)) – динамическая характеристика СИТ, представляющая собой зависящее от круговой частоты отношение преобразования Фурье выходного сигнала СИТ к преобразованию Фурье его входного сигнала при нулевых начальных условиях.
(комплексный коэффициент преобразования (передача)) – динамическая характеристика СИТ, представляющая собой зависящее от круговой частоты отношение преобразования Фурье выходного сигнала СИТ к преобразованию Фурье его входного сигнала при нулевых начальных условиях.
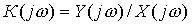 .
.
Связь между передаточной функцией и амплитудно-фазовой характеристикой можно представить следующим образом
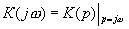 .
.
Встречается понятие – приведенная комплексная частотная характеристика 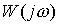 , которая равна
, которая равна 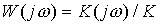 .
.
Совокупность амплитудно-частотной и фазо-частотной характеристик.
Амплитудно-фазовая характеристика может быть представлена в алгебраической форме
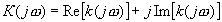 ;
;
или в показательной форме
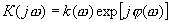 ,
,
где 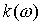 – амплитудно-частотная характеристика СИТ, представляющая собой зависимость модуля коэффициента преобразования от частоты;
– амплитудно-частотная характеристика СИТ, представляющая собой зависимость модуля коэффициента преобразования от частоты; 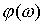 – фазо-частотная характеристика СИТ, представляющая собой зависимость аргумента коэффициента преобразования от частоты.
– фазо-частотная характеристика СИТ, представляющая собой зависимость аргумента коэффициента преобразования от частоты.
Импульсная характеристика СИТ
Импульсная характеристика СИТ, g(t) – временная динамическая характеристика СИТ, представляющая собой его отклик на испытательный сигнал в виде дельта-функции 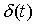 .
.
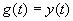 ,
,
если на вход СИТ действует испытательный сигнал 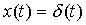 ,
,
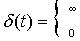
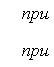
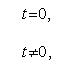
при условии, что
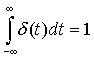 .
.
Импульсную характеристику можно получить из представленных выше характеристик. Например,
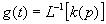 ,
,
где 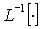 – обратное преобразование Лапласа.
– обратное преобразование Лапласа.
Переходная характеристика
Переходная характеристика СИТ h(t) – временная динамическая характеристика СИТ, представляющая собой его отклик на испытательный сигнал в виде единичной ступенчатой функции.
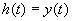 ,
,
если вход СИТ подается испытательный сигнал 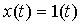 ,
,
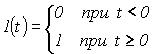
Связь переходной характеристики и импульсной можно представить следующими соотношениями: