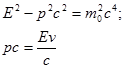Релятивистская энергия

Найдем релятивистское выражение для энергии. Будем действовать по аналогии с нерелятивистским случаем:

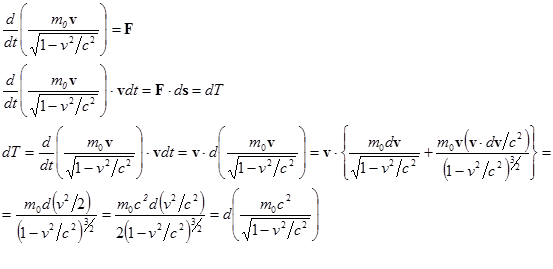
Интегрирование дает:

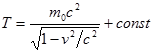
Из начального условия (Т = 0 при v = 0) получаем:

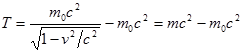
Где mc² - полная энергия тела.

Таким образом, разница полной энергии тела и энергии покоя равна кинетической энергии тела.

Предположим, что наши два тела с равными массами (те которые столкнулись) можно «видеть» даже тогда, когда они оказываются внутри тела М. Масса тела М, как мы обнаружили, равна не 2m₀, а равна 2m_w. Значит, избыток массы составного тела равен привнесенной кинетической энергии. Это означает, что у энергии есть инерция. Т.е. энергия эквивалентна массе. На самом деле такое рассуждение является совершенно общим; в появлении избыточной массы участвуют все виды энергии, например, потенциальная энергия взаимодействия частиц.

Теперь обратимся к вопросу: нужно ли добавлять к кинетической энергии m₀c² и говорить с этих пор, что полная энергия объекта равна mc²?

Если бы нам видны были составные части с массой покоя m₀ внутри объекта М, то можно было бы говорить, что часть массы М есть механическая масса покоя составных частей, а другая часть - их кинетическая энергия, третья - потенциальная и т.д. Но никакими способами нельзя разглядеть внутри М какие-то составные части. А потому возникает новая идея: нет нужды знать, как тела устроены изнутри; нельзя и не нужно разбираться в том, какую часть энергии внутри частицы можно считать энергией покоя тех частей, на которые она распадается. Неудобно, а порой и невозможно разбивать полную энергию mс² тела на энергию покоя внутренних частей, их кинетическую и потенциальную энергию; вместо этого мы просто говорим о полной энергии частицы. Мы «сдвигаем начало отсчета» энергии, добавляя ко всему константу m₀с², и говорим, что полная энергия частицы равна ее массе движения, умноженной на с².

Легко обнаружить, что скорость v, импульс р и полная энергия Е довольно просто связаны между собой. Исходные соотношения:

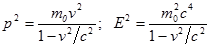
Важными для практики оказываются два выражения: