Теоретический материал. Теория графов в последнее время широко используется в различных отраслях науки и техники, особенно в экономике и социологии

Теория графов в последнее время широко используется в различных отраслях науки и техники, особенно в экономике и социологии.

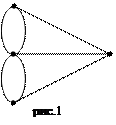Основы теории графов разработал Леонард Эйлер, решавший задачу о разработке замкнутого маршрута движения по мостам в г. Кенигсберге. При решении задачи он обозначил каждую часть суши точкой, а каждый мост – линией, их соединяющей. В результате был получен граф (рис. 1).

Эйлер доказал, что такая задача решения не имеет. Быстрое развитие теория графов получила с созданием электронно – вычислительной техники, которая позволяла решить многие задачи алгоритмизации.

Пусть на плоскости задано некоторое множество вершин Х и множество 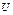соединяющих их дуг. Графом называется бинарное отношение множества Х и множества 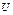: 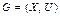, или, иначе .

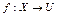Граф называется ориентированным, если указано направление дуг и неориентированным, если такое направление не указано. Примером неориентированного графа является карта дорог.

Петля – это ребро, у которого начальная и конечная вершины совпадают. Две вершины называются смежными, если существует соединяющая их дуга. Ребро называется инцидентным вершине, если оно выходит или входит в вершину.

Степенью (валентностью) вершины называется число инцидентных ей ребер. Кратностью пары вершин называется число соединяющих их ребер или дуг.

В изображении графа имеется относительно большая свобода в размещении вершин и выборе формы соединяющей их ребер. Поэтому один и тот же граф может быть представлен (на плоскости) по-разному.

Графы называются изоморфными, если между множествами их вершин существует взаимно однозначное соответствие, такое, что вершины соединены ребрами в одном из графов в том и только том случае, когда соответствующие им вершины соединены в другом графе. Если ребра графа ориентированы, то их направление в изоморфных графах также должно соответствовать друг другу.

В теории графов есть понятие обход графа. Это маршрут, содержащий все ребра или вершины графа и обладающий определенными свойствами. Наиболее известными обходами графа являются Эйлеровы и гамильтоновы цепи и циклы.