Геометрическое распределение

Биномиальное распределение

X=0,1,2,…n –бином-ое распредел. Pk=P[x=k]=CknPkqn-k G(z)=P0+P1z+P2z+…+Pkzk…

=∑ CknPkqn-kzk = ∑ Ckn(pz)kqn-k = (pz+q)n

G’(z)=n(pz+q)n-1p G’(1)=M[x]=np

G”(z)=n(n-1)( pz+q)n-2p2 G”(1)=n(n-1)p2

M[x]=np = ∑kPk D[x]=npq = ∑(k-np)2Pk

Распределение Пуассона

Pk=P[x=k]= (λk\k!)e-λ

G(z)= ∑(λk\k!)e-λzk=e-λ∑( λz)k\k!= e-λ ezλ= eλ(z-1)

G’(1)= eλ(z-1) λ G’(1)= λ= M[x]=m

G”(z)= eλ(z-1) λ2 G”(1)= λ2 M[x]=λ

D[x]= λ2+ λ- λ2= λ

Геометрическое распределение

X=0,1,2….

P_k=P[x=k]q^kp

G(z)= ∑P_kz^k=∑q^kpz^k=p∑(qz)^k=P*1\(1-qz)=P\(1-qz)

M[x]=1\p D[x]=q\p²

№4.Теорема сложения и умножения вероятности.

P(A/B)- условная вероятность события A при условии , что соб.B произошло.

1) 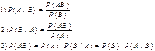1)усл.вер-ть P(A/B) 2) усл.вер-ть P(B/A) 3) -теорема умножения для зависимых соб.А и В. Если соб.А не влияет на вер-ть соб.В и наоборот,то они независимы: P(A/B)=P(A); P(B)=P(B/A) => P(AB)=P(A)*P(B) – вер-ть произ-ния соб-й равна произ-нию вер-тей.

P(ABC)=P(H)*P(A/H)=P(BC)*P(A/BC)=P(C)*P(B/C)*P(A/BC) (ВС обозначили за Н)

Опр-е независимости для А,В и С- соб. А,В и С назыв.независимыми в совокупности,если выполн.след усл-я: 1)Если попарно независимы P(AB)=P(A)*P(B), P(BC)=P(B)*P(C), P(AC)=P(A)*P(C). 2)P(ABC)=P(A)*P(B)*P(C)

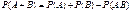- ф-ла сложения вер-тей

Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

№5. Формула полной вероятности и формула Байерса.

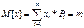Пусть Н₁,Н₂…Н_k подмножества пространства эл.соб-й W, такие что:

1)H_i H_j=Æ, i≠j и I,j=1,2,…,k 2)H1+H2+…+H_k = W

В этом случае говоря,что сис-ма подмножеств Н₁,Н₂…Н_k образует разбиение множества W. Для любого соб.А,являющего подмножеством W, верна ф-ла полной вер-ти

События H_i называются гипотезами по отношению к соб.А,а вер-ти Р (H_i) трактуются как доопытные вер-ти гипотез, причем å Р (H_i)=1.

Формула БайесаЕсли известно, что соб.А произошло, то апостериорные вер-ти гипотез H_i ,очевидно, должны быть пересчитаны, так как появилась доп.информация. Апостериорные вер-ти гипотез H_i ,при условии, что А произошло,вычисляются по ф-е Байеса: 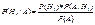,i=1…k, где Р(А) определяется по ф-е полной вер-ти.

№6.Дискретные случайные величины. Ряд распределения. Числовые характеристики.Пусть (W,F,P) – дискретное вероятностное пространство. Числовая ф-ция Х=Х(W) определенная на пространстве эл.соб-й Wназывается дискретной случ.величиной. Сис-ма равенств: P[x=x_i]=р_i, i=1,2…n,.. определяет распределение вероятностей дискретной слу.величины Х. Очевидно,что р_i≥0, å р_i=1 Простейшей формой закона распределения дискретной величины является ряд распределения.

Xi	x1	…	хn	…
P(x=xi)	P1	…	pn	…

Графической интерпретацией ряда распределения является многоугольник распределения.

Функция распределения случайной величины. Для непрерывных случайных величин применяют такую форму закона распределения, как функция распределения. Функция распределения случайной величины Х называется ф-ция F(х), определяемая для любого действительного зн-я х,как вер-ть события [Х<х], т.е. F(х)=Р[Х<х]. Функция распределения обладает следующими свойствами: 1.0≤F(х)≤1 2.F(x)- неубывающая ф-ция х, если х₂>х₁,то F(х₂)>F(х₁) 3. F(-∞)=0 F(+∞)=1 Функция может быть изображена в виде графика. Для непрерывной величины это будет кривая изменяющееся в пределах от 0 до 1, а для дискретной величины - ступенчатая фигура со скачками.

Числовые характеристики случайной величины.

Математическое ожидание случайной величины. Пусть Х- дискретная случ.величина, принимающая зн-я х₁,х₂.. с вероятностями р₁,р₂.. Математическое ожидание M[x] случ.величины X опередляется формулой ↓ Свойства мат.ожидания: 1.M[c]=c 2.M[c*X]=c*M[X] 3.M[c+X]=c+M[X] 4.M[X+Y]=M[X]+M[Y] мат.ожидание суммы равно сумме мат.ожиданий

Х- некая дискр.случ.вел-на. Рассмотрим h(X) – функцию от Х. Мат.ожидание функции случ.вел-ны:

Дисперсия Дисперсия (D[x]) характеризует разброс случ.величины Х относительно ее математического ожидания и вычисляется:

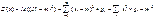
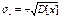Дисперсия случайной величины всегда величина положительная. Среднеквадратическое отклонение.

Св-ва дисперсии: 1)D[X]≥0 2)D[c]=0 3)D[X]=0 4)D[cX]=c²D[X] 5)D[X+c]=D[X] 6)D[X+Y]=D[X]+D[Y]

Начальным моментом k-го порядка α_k случайной величины X называется математическое ожидание k-ой степени случайной величины X.

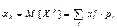k=1 α₁=M[X]=m ; k=2 α₂=M[X²]

Центрированная случайная величина - это величина, равная X’=X-MX. Покажем, что математическое ожидание MX’ равно 0.

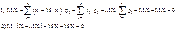
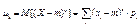Центральным моментом k-го порядка μ_k случ.величины Х называется матем.ожидание k-ой степени отклонения Х от ее мат.ожидания m

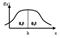
Модой d_x дискретной случайной величины, принимающей зн-я x₁,x₂.. , называется такое зн-е случ.величины,кот.имеет наибольшую вер-ть: P[X= d_x]=max P[X=x_k] (при условии что x_k –единств.зн-е,удовлетвор.этому условию.

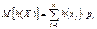Медианой h_x случайной величины называется такое ее значение, для которого окажется ли случайная величина меньше этого значения. Квантиль порядка р=0,5 назыв. медианой h_x случ.вел-ны Х (h_x=х_0,5) Для непрерывной случайной величины медиана это абсцисса точки, в которой площадь под кривой распределяется пополам.

№7.Повторение испытаний. Схема Бернулли. Биномиальное распределение. Формула Пуассона.Последовательные испытания наз-ся независимыми, если вероятность осущ-я любого исхода в n-ом по счету эксперименте не зависит от исходов предыдущих испытаний. Схема испытаний Бернулли: 1. послед-ть независимых испытаний с двумя исходами («успех» и «неуспех»); 2. эксперимент проводится n раз в неизменных усл-ях, т.е. вероятности «успеха»(p) и «неуспеха»(1-p=q) неизменны.

n-число испытаний, k-число благоприятных исходов, событие А – «успех», Х – случ.величина, обозначающая число «успехов» в n испытаниях по сх. Бернулли (Х=0,1,2,…n).

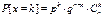- формула Бернулли, где C_n^k-число случайного размещения события А в послед-ти из n мест. Соответствующее распр-е случ.вел.Х наз-ся биномиальным распр-ем.

Свойства бином.распр-я:

1. ;

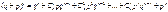2. 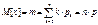-матем.ожидание

3. 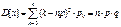-дисперсия.

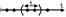Приближенная формула Пуассона:

.

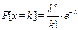(-интенсивность потока):

= = ;

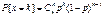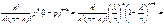
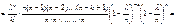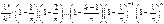Берем предел

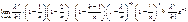
№3.Классическая схема равновероятных событий.

Если W содержит конечное число эл.соб-й,например N соб-й, причем все эл.исходы равновозможны,т.е. p(w_i)=1/N, i-1,2,..,N, то P(A)=|A|/|W|, где |A|-кол-во эл.исходоы,составляющих множество А, а |W|- число всех эл.исходов данного эксперимента. |W|=N Такая ф-ла назыв. классическим определением вер-ти (Если эл.исходы равновозможны, то вер-ть соб.А равна отношению числа исходов,благопритствующих соб.А, к числу всех эл.исходов)

№8.Распределение Пуассона. Физическая модель, приводящая к распределению Пуассона.

Если n достаточно велико, а p мало, то формулу Пуассона исп-ют вместо точных биномиальных формул для вероятностей k успехов в n испытаниях. При n→∞, p→0 при условии λ=np=const-интенсивность потока: = = ; .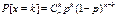

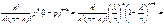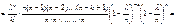
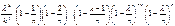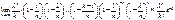Случ.вел.Х наз-ся распределенной по закону Пуассона с параметром λ>0, если ее возможные значения равны 0, 1, 2….., а соответствующие вероятности определ-ся формулой .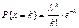

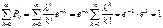; M[x]=λ,D[x]=λ
Физическая модель, приводящая к распределению Пуассона:Точка-событие, послед-ть точек – поток событий. Возьмем некот.интервал длины t. Вер-ть того, что на инт-ле t произойдет ровно n событий: Pn(t)=? 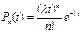.Простейший (Пуассоновский) поток событий, если он: Стационарный – если Pn(t) не зависит от того, где выбран интервал длины t.

Отсутствует последствие (память) - если Pn(t) не зависит, не изменяется от того, сколько событий произошло на смежных соседних интервалах. Ординарный – можно выбрать столь малый интервал ∆t, что вероятность Pn(∆t) пропорциональна длине интервала 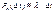, а вероятность двух, трех и т.д. событий одновременно – есть величина бесконечно малая: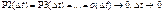

Док-во: Вер-ть того, что 1 событие не произойдет: 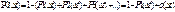Рассмотрим инт-л длины (t+∆t): => ;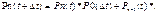
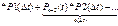
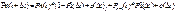
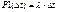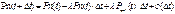
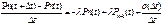
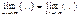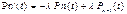
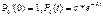, сл-но с=1, .
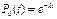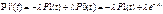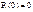; ,сл-но 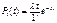.Сл-но 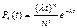- вер-ть того, что на инт-ле t произойдет n событий, λ-среднее число событий,кот. происходит на 1чном инт-ле.

№10.Вероятность в непрерывных пространствах эл событий и ее св-ва. Геометрические вер-ти.

Пусть 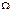- непрерывное простр-во.

Алгебра событий (F) – это система подмножеств W, W={ω_1,,ω₂,…} кот.удовл-ет следующим свойствам: 1. ΩÎF, ÆÏF; 2. A,BÎF => A+B 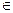F, ABÎF, не А и не ВÎ F; 3. F 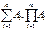явл-ся сигма-алгеброй, если определены операции. Для счетного числа событий.

Пусть событие А 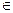F, тогда Р(А) -вероятность, число, которое должно удовл-ть:
1.P(Ω)=1; 2.АÎВ,Р(А)≥0; 3.А∙В≠0, A+BÎF=>P(A+B)=P(A)+P(B).

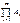=ÆÞ

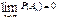
Свойства вероятностей: 1.Р(Æ)=0-вер-ть невозможного события 2. 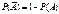3. АÌВ- если А-следствие В, то Р(А)<=Р(В). 4. P(A+B)<=P(A)+P(B) 5. непрерывности: если

А1ÌА2Ì…ÌАnÌ… ,то ;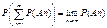
если А1ÉА2É…ÉАnÉ…, то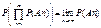

Геометрические вер-ти, Для любого подмножества А можно посчитать его площадь: Р(А)=площ.А/площ.Ω. Т.к. вер-ть пропорцион-на площади, то чем > лощадь, тем > вероятность попадания в событие. P(A)=mes(A)/mes(Ω) – мера А/мераS.

14.Мат. ожидание и дисперсия суммы случайных величин.

M[X]=m_x= 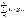M[Y]=m_y=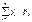

(M[X], M[Y])-центр распределения.Пусть X и Y - случ. вел. С конечными мат. ожиданиями. Мат. ожидание их суммы равно сумме их мат. ожиданий. M[X+Y]=

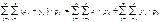
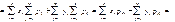M[X]+M[Y] Пусть X и Y- взаимно независимые случ. вел с конечными мат. ожиданиями. Мат ожидание произведенияXY равно произведению их мат. ожиданий. M[XY]= 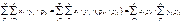=M[X]*M[Y].
Это правило распространяется на любое конечное число взаимно независимых случ. величин. Заметим, то последнее равенство для зависимых случ. величин, вообще говоря, е выполняется. Пусть X и Y- случ. Вел с совместным распределением, задаваемым таблицей (1). Условное мат. ожидание случ. dел. X при условии, что Y принимает заданное значение Y = yj, вычисляется по формуле: M[X/Y=yj]=
Дисперсия суммы случайных величин:D[X+Y] z=X+Y => D[z]=M[(z-m_z)²], а m_z=m_x+m_y

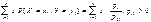D[z]= M[((X-m_x)+(Y-m_y))²]= M[(X-m_x)²]+2 M[(X-m_x)(Y-m_y)]+

+M[(Y-m_y)²]=D[X]+2cov(X,Y)+D[Y]

Таким образом: D[X±Y]=D[X]+D[Y]±2cov(X,Y) Если X и Y независимые, то cov(X,Y)=0 => D[X±Y]=D[X]+D[Y] Рассмотрим D[aX±bY]=a²D[X]+b²D[Y]±2abcov(X,Y)

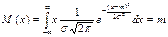
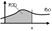
№11.Непрерывные случайные величины.Случайная величина Х называется непрерывной, если для нее существует неотрицательная частично-непрерывная функция f(x) , удовлетворяющая для любых значений x равенству 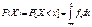(случайные величины, возможные значения которых образуют некоторый интервал). f_x - плотность распределения вероятностей (плотность распр-я единичной массы на инт-ле). Св-ва: если x 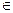[a;b]: 1. f(x)>=0; 2. ; ; .

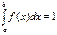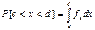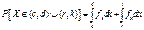если 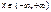: 1. f(x)>=0; 2. 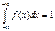; 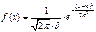- норм.распр-е.
F(x) – ф-я распределения для непрер.случ.величин, определена на всей числовой оси, ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х. Свойства: 1)0<=F(X)<=1;2)F(-∞)=0 3)F(+∞)=1;4)F(X)-неубыв.ф-я 5) :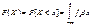

6)f(X)=dF(X)/dx 7) -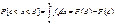

вер-ть попадания в [c;d].
Мат.ожидание: 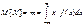, , 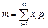где f(x)dx=P[x<X<x+dx] – элемент вер-ти. Свойства: 1.M[cX]=cM[X] 2.M[c+X]=c+M[X] 3.M[X+Y]=M[X]+M[Y]
4.X=j(x),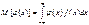

Дисперсия: ,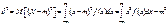
Начальный момент k-го порядка -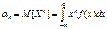
Центральный момент k-го порядка -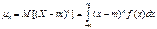

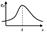Асимметрия- 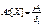,где δ- ср. квадратич. отклонение
Эксцесс – 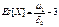хар-ет форму распред-я в окрестности вершины
Квантиль – абсцисса (точка на оси х), которая слева от себя отделяет площадь под графиком плотности, равную Р. F(x_p)=P – порядок квантили. 1. 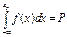; 2. F(X)=P[X<x]. Квантиль порядка 0,5 – х_0,5 – для любого распр-я наз-ся медианой (h) (отделяет ½ площади под плотностью слева и справа). Если распр-е симметрично, то h совпадает с мат.ож. m.
Мода (d) – абсцисса, при кот. плотность распр-я имеет максимум: f(d)=max

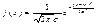№12.Нормальное распределение.Нормальное распределение N(m,s²) имеет плотность, определяемую формулой:

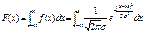Функция распр-я F(х)норм.распр-я равна:

Параметры m и s² норм. распр-я равны соответственно мат.ожиданию и дисперсии случ.вел-ны Х:

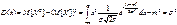Центральные моменты норм.распр-я можно вычислить из рекуррентного ур-ния: μ_k+2=(k+1)s²μ_k , k=0,1,2,… (причем μ₀=1). Для норм.распр-я все центр.моменты нечетного порядка равны 0. Коэффициент ассиметрии a_x норм.распр-я равен 0. a_x=μ₃/s₃ Из формул получаем: μ₂=s², μ₄=3s⁴ Коэффициент эксцесса равен 0: е_х= μ₄/s⁴-3=0. Стандартизированное нормальное распределение и его свойство. Норм.распр-е с нулевым мат.ожиданием и дисперсией,равной 1, назыв.стандартным норм.распр-нием: Х~ N(0,1). Ф-ла плотности j(х) станд.норм.закона равна

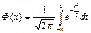
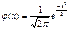, -¥<x<¥. А функция распр-я:
Так как плотность распр-я станд.норм.закона j(х) симметрична относ-но оси ординат,то для ф-ции распр-я Ф(х) справедливо след.св-во: Ф(-х)=1-Ф(х)

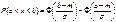Зн-я функции Ф(х) использ.при вычислении вер-ти попадания норм.распр-ной случ.величины Х в заданный интервал:

В практич.задач часто приходится вычислять вер-ть попадания случайной величины Х~ N(m,s²) в интервал, симметричный отн-но ее математического ожидания m:

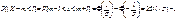Используя получ.рез-тат,вычислим вер-ть отклоенения от мат.ожидания норма.распр-ной случ.вел-ны на вел-ну,равную трем средневкадратич.отклонениям, 3s: P[|X-m|<3s]=2Ф(3)-1»2*0,9987-1»0,9973 Этот результат известен как «правило трех сигм»: с вер-тью 0,9974(практически=1) зн-е нормально распределенной случ. вел-ны лежит в интервале (m-3s;m+3s) Правило трех сигм это правило часто используется для подтверждения или отбрасывания гипотезы о нормальном распределении случайной величины.

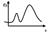
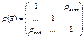
№13. Системы дискретных случайных величин.

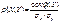
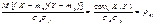Рассмотрим две случайные величины X и Y, определенные на одном дискретном вероятностном пр-ве (Ω,F,P). Обозначим значения, кот. принимает случ. величина Х через х1, х2, …, хn, а значения случ. величины Y через y1,y2,…,yn. Распределение вероятностей X и Y обозначим соответственно p_х1, p_х2, …, p_хn и p_y1, p_y2, …, p_yn. Вер-ть события, состоящего в том, что Х=хi и Y=yj, обозначим как P[X=xi; Y=yj]=p_ij. Опр Система равенств P[X=xi; Y=yj]=p_ij, p_ij>0, 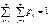, p_ij=1, i=1,2, .., n, j=1,2,..,m определяет совместное распределение дискретных случайных величин X и Y или системы 2-ух дискр. случ. величин (X,Y). Распределение системы 2-ух дискр. случ. вел. (X,Y) записывают в виде таблицы распределения.

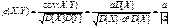Суммируя вер-ти p_ij по строкам, получим рапределение случ. вел X: 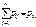, i=1,2, .., n, суммирование вер-тей p_ij по столбцам дает распределение случ. вел. Y: 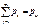, j=1,2,..,m. Аналогично определяется

распределение системы более чем 2-ух случ. вел. Условные распределения: Условная вер-ть события Х=хi при условии, что Y=yj (p_yi>0) определяется формулой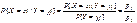

Система равенств (1) при , i=1,2, .., n задает условное распределение случ. вел. X при условии,что случ. вел Y принимает заданное значение Y= yj. Опр Определение независимости случ. величин. Пусть таблица (1) суть таблица распределения случ. вел X и Y. Случ. вел-ны X и Y наз. независимыми,если события X=xi и Y=yj независимы для всех i и j таких, что 1≤i≤n, 1≤j≤m, т.е. 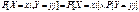или

p_ij= p_xi´p_yj.Если X и Y независимые случ. вел., то таблица распределения имеет вид таблицы умножения. Аналогично определяется взаимная независимость более чем 2-ух случ. вел. Для независ. случ. вел. Условные вер-ти равны безусловным вер-тям P[X=x_i/Y=y_i]=P[X=x_i], P[X=x_i/Y=y_i]=P[Y=y_i]

Опр Случайные величины X1, X2,..,Xn определенные на одном дискретном вероятностном пр-ве наз. взаимно независимыми, если для любой комбинации значений x_i1, x_i2, .., x_in..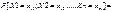

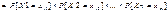
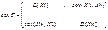Опр Пусть случ. величины X и Yимеют конечные дисперсии. Ковариацией X и Y наз.. математическое ожидание произведения центрированных случ. величин (X-m_x) и (Y-m_y): cov(X,Y)=M[(X-m_x)(Y-m_y)]= M[XY]-m_xM[Y]-m_xM[X]+m_xm_y=M[XY]-m_xm_y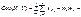 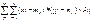(Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от её математического ожидания) Св-ва cov:1.Если X и Y независимые случ. вел, то cov(X,Y)=0, обратное же неверное, т.е. если cov(X,Y)=0, это не значит,что величины независимы. . cov(aX,bY) = abcov(X,Y), где a и b – константы 3.cov(X,Y)≤ 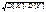Это неравенство явл. следствием неравенства Коши-Буняковского: (M[XY])²≤M[X²]*M[Y²] Док-во нер-ва: Рассмотрим очевидное неравенство M[(aX+Y)²] ≥0, где а-любое действительное число, а≠0. Преобразуем левую часть этого неравенства, используя св-ва мат. ожиданий M[(aX+Y)²]=M[a²X²+2aXY+Y²]=a²M[X²]+2aM[XY]+M[Y²]≥0 Т. К. Полученный относительно a трехчлен принимает только неотрицательные значения, то его дискриминант будет меньше или равен нулю: 4(M[XY])²-4M[X²] *M[Y²]≤0 Отсюда следует неравенство (M[XY])²≤M[X²]*M[Y²]. Заменим X на (X-m_x), а Y на (Y-m_y), получим: (M[(X-m_x)(Y-m_y)])²≤M[(X-m_x)²]*M[(Y-m_y)²] или (cov(X,Y))²≤D[X]*D[Y] Механическая интерпретация.n-мерные случ. величины(x1, x2,..,xn)- n-мерный случ. вектор (x1, x2,..,xn)= 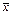M[ 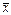] =(M[x1],…, M[xn]), т.е мат. ожидание вектора равняется вектору мат. ожиданий. Cov(Xi;Yj)=M[(Xi-m_xi)(Yj-m_yj)], j,i=1,..,n

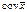-ковариационная матрица (симметрична) 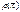-корреляционная м-ца(симметрична) D[x1+x2+x3]=D[x1]+D[x2]+D[x3]+2cov(x1,x2)+2cov(x2,x3)+2cov(x1,x3)

№15.Коэффициент корреляции как характеристика статистической связи. Некоррелицированность и независимость с.в.

В качестве меры линейной зависимости между случ. величинами X и Y используют коэффициент корреляции, вычисляемый по формуле Св-ва коэфиициента корреляции:1. 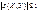Док-во: рассмотрим систему 2-ух случ. вел: (X,Y) Проведем нормировку (стандартизацию), т.е. M[X]= m_x D[X]=σ_x² X^x_{нормиров}=(x-mx)/σx Нормированная величина – это тогда, когда M[Y]=m_y D[Y]= σ_y² Y_{yнормиров}= (y-my)/σy m_ч=0, а σ_x=1 Cov(X^x,Y^y)=M[{(x-mx)/σx}]*M[{(y-my)/σy}]=
2. Если X и Y – незав. случ. вел, то r(Х,У)=0, причем обратное неверно 3.Если X и Y связаны линейной функциональной зависимостью: Y=aX+b, где a,b – const , a≠0,то 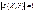Док-во: Т.к M[Y]=aM[X]+b=am_x+b, то имеем cov(X,Y)=M[(X-m_x)*(Y-m_y)]=M[(X-m_x)(aX+b-am_x-b)]=M[(X-m_x)a(X-m_x)]=aD[X] Вычислим дисперсию случ. вел. Y=aX+b D[Y]=D[aX+b]=a²D[X] Таким образом, коэффициент корреляции равен: Следовательно, r(Х,У)=1, если a>1 и r(Х,У) =-1, если a<0 Т.е коэффициент корреляции является показателем линейной зависимости, но если ρ_xy=0. это не значит,что между ними нет никакой связи, это значит, что нет линейной зависимости.Если коэффициент корреляции между случ. вел. X и Y равен 0, то говорят, что X и Y некоррелированны. Некоррелированность случ. вел X и Y означает только, что между ними нет линейной зависимости и не означает статистическую независимость случ. вел X и Y.

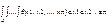
№18.Функции случайных величин.Функции дискретных случайных величин. Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайной величины Х y=φ(x)

Функции непрерывных случайных величинаний. M{}

y=φ(x) – непрерывная дифференцируемая монотонная ф-ция

1.Монотонно возрастает (Лекции 13 рисунок)

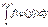
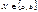{y<Y}равносильно{x<X}

{x<X}: F_x(x)=P(x<X)= - ф-ция распределения

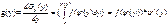P(y<Y)=G_y(y)-ф-ция распределения

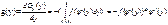
2.Монотонно убывает (Лекции 13 рисунок)
X>x

P(y>Y)=G_y(y)
Функция плотности вероятности для функции случайной величины y=φ(x) -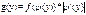

Математическое ожиданиеy=φ(x) 1. Пусть X- дискрет случ. вел, тогда y_n= φ(x_n) ;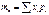
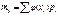
2. Пусть X –непрер. Случ. Вел

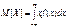
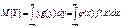
Для вычисления числовых характеристик неслучайной ф-ции случайной величины не надо знать закона распределения зависящей от X случайной величины Y, а достаточно знать закон распределения случайного аргумента т. ожиданий. M{}

Пример.

X=y³

x	-2	-1
P	0.1	0.15	0.3	0.05	0.4

X→Y

x	-8	-1
P	0.1	0.15	0.3	0.05	0.4

x
P	0.3	0.2	0.5

Y=x²

№16.Системы 2-ух непрерывных случ. вел. Определение ф=ции распределения и плотности, условные распределения, зависимость и независимость случ. вел. Числовые характеристики.

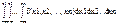
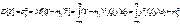
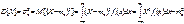Пусть на вероятностном пр-ве (Ω,F,P) заданы непрерывные случ. вел X1=X1(ω), X2=X2(ω),.., Xn=Xn(ω), ωÎΩ. Опр Совместной ф-цией распределения F(x₁, x₂,…, x_n) случ. вел X1,X2,..,Xn наз-ся вероятность события [X1<x1;X2,x2;…;Xn<xn]: F(x₁, x₂,…, x_n) =P [X1<x1;X2,x2;…;Xn<xn] Фукция распределения: F(X,Y)=P[X<x,Y<y] Если пользоваться геом. интерпретацией системы образом случ. точки, то ф-ция распред. есть не что иное, как вер-ть попадания случ точки (X,Y) в бесконечный квадрат с вершиной в точке (x,y), лежащий левее и ниже ее.()ки, то ф-ция распред. Е 1.Ф-ция распред. Есть неубывающая ф-ция обоих своих аргументов,т.е при x2>x1, F(x2,y)≥ F(x1,y) при y2>y1 F(x,y2) ≥F(x,y1) 2.Повсюду на -∞ ф-ция распред. равна нулю: F(x,- ∞ )= F(-∞ ,y)= F(-∞ ,- ∞ )=0 3. F(x,+ ∞ )=F1(x1(): распред. я обоих своих аргументов,т.е), F(+∞ ,y)=F2(y) 4. F(+∞ ,+ ∞ )=1 2()Неотрицательная ф-ция n переменных f(x₁, x₂,…, x_n) наз-ся совместной плотностью распределения случ. величин X1,X2,..,Xn , если их совместная ф-ция распределения может быть представлена в виде F(x₁, x₂,…, x_n) =Геометрически функцию f(x,y) можно изобразить некоторой поверхностью – поверхность распределения. Если пересечь поверхность распред. Плоскостью, перелелльной плоскости XOY, и спроектировать полученное сечение на плоскость XOY, получится кривая, в каждой точке которой плотность расред. постоянна. Плотность распределения имеет след. св-ва: 1. f(x₁, x₂,…, x_n) ≥; (это ясно из того, что плотность распред. есть предел отношения двух неотриц. величин: вероятности попадания в прямоугольник и площади прямоугольника) 2. 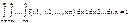; (геометрически это cв-во означает ,что полный объем тела, ограниченного поверхностью распределения и плоскостью XOY равен едицице.) 3.Если ф-ция определена, вектор попадет в некоторую область,тогда вер-ть определяется: P[(x1,x2,..,xn)ÎG]=
(геометрически вер-ть попадания в область G изображается объемом цилиндрического тела, ограниченного сверху поверхностью распред и опирающегося на область G. Зная совместную плотность распределения f(x₁, x₂,…, x_n) случ. вел X1,X2,..,Xn можно найти плотность распред. каждой случ. вел. Для двумерного вектора (X1,X2) с плотностью f(x₁, x₂) распределение случ. вел X1, f₁(x₁) равна f₁(x₁) = 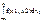, а плотность распред. случ. вел. X2, f₂(x₂) равна f₂(x₂) = 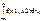Опр Случ. величины X1,X2,..,Xn наз-ся независимыми, если для любых действительных переменных x₁, x₂,…, x_n, F(x₁, x₂,…, x_n) =F1(x₁)* F2(x₂)*…* Fn(x_n), где Fi(x_i)-ф-ция распред. случ. вел Xi, i=1,2..,n Равносильное определение независимости случайных величин X1,X2,..,Xn записывается так f(x₁, x₂,…, x_n) =f₁(x₁)* f₂(x₂)*…* f_n(x_n), где f_i(x_i)-плотность распред. случ вел. Xi, i=1,2..,n f₁(x)= 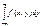f₂(y)=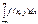

X и Y независимы, если

f(X,Y) = f₁(x)* f₂(y) X и Y независимы, если f(X/Y)= f₁(x); f(Y/X)= f₂(y) Условные плотности распределения.Распределение Y, если X принимает какое-либо значение f(Y/X) Распределение X, если Y принимает какое-либо значение f(X/Y) Условная ф-ция и распределения.Распред. X, при условии Y=y

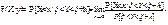f(X/y)=f(x,y)/f2(y) f(Y/x)= f(x,y)/f1(x)

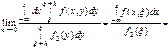
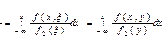
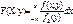
Числовые характеристики:1. Мат ожидание: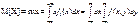

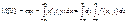
т. ожиданий. M{} т. ожиданий. M{}2.Дисперсия

Св-ва:
M[X+Y]=M[X]+M[Y] M[X*Y]=M[X]*M[Y], если X и Y независимые D[X+Y]]=D[X]+D[Y], если X и Y независимые

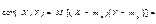3.Ковариация

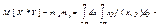
4.Коэффициент корреляции

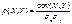
(Св-ва ковариации билет 13, св-ва корреляции билет 15)

№17.Нормальный закон на плоскости.

Двумерное нормальное распределение –это распределение системы двух случайных величин (X,Y) с плотностью распределения f(x,y), определяемой формулой.

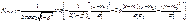Плотность распределения случ. вел X, f₁(x), вычисляется интегрированием f(x,y) по y:

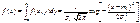Аналогично вычисляется плотность распред случ вел Y,f₂(y):

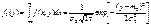Формула (1) показывает,что в случае двумерного нормального распределения с плотностью (1) компоненты X и Y имеют нормальное распред, причем M[X]=m₁, D[X]=σ₁², M[Y]= m₂, D[Y]=σ₂²

Ковариация X и Y равна

cov(X,Y)=M[(X-m₁)(Y-m₂)]= = 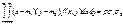Отсюда следует,что параметр ρ в (1) есть коэффициент корреляции

Св-ва:

1.Если (X,Y) имеет норм. распред.:

Каждая компоненты этого распределения также имеет нормал. распределение

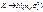
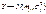
2. Если ρ=0 => f(x,y)= f₁(x) ´ f₂(x) => X и Y – независимые

3.Условная плотность распределения:

f(X/y) и f(Y/x) – нормальные плотности

Геометрически плотность f(x,y) двуменого нормального распределения (1) представляет «холмообразную » поверхность. Проекция вершины холма на плоскость xOy имеет координаты (m₁, m₂) Эта точка называется центром рассеивания.

Сечение поверхности Z=f(x,y) плоскостями , параллельными плоскости xOy, есть кривые, определяемые ур-нием:

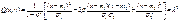, где λ – const. Проекциями этих кривых на плоскость xOyбудут эллипсы. Т.к. плотность f(x,y) имеет на этих кривых постоянное значение, то соответствующие эллипмсы наз. эллипсами равных вероятностей

Эллипсы равных вероятностей имеют общий центр – центр рассеивания с координатами(m₁, m₂) и общие оси симметрии (они наз главными осями ξ и η)

№19. Функции нескольких случайных величин. Вычисление мат ожиданий и дисперсий для суммы случайных величин.

Математическое ожидание

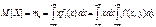
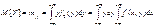
Дисперсия

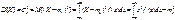
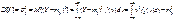
Св-ва мат. ожидания и дисперсии:

1.M[X+Y] = M[X] + M[Y]

2.M[X*Y] = M[X] * M[Y]

3.D[X+Y] = D[X] + D[Y]

Коэффициент ковариации

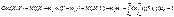
Св-ва мат. ожидания и дисперсии:

1.Если X и Y независимы, то Cov(X,Y) = 0 (обратное неверно!)

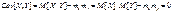
2.Cov(aX,bY) = ab*Cov(X,Y), где a и b – константы

3.Cov(X,Y)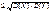

Коэффициент корреляции

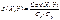
Св-ва мат. ожидания и дисперсии:

1.|ρ(X,Y)| ≤ 1, этот результат следует из свойства 3 для ковариации случайных величин X и Y.

2.Если Х и Y – независимые случайные величины, то ρ(X,Y) = 0 (по свойству 1 для ковариации)

3.Если X и Y связаны линейной функциональной зависимостью: Y=aX + b, где a и b – константы, а ≠ 0, то |ρ(X,Y)| = 1

Теорема Бернулли.

Пусть А – случайный исход некоторого экспериментов, P(A)=p – вероятность этого исхода. Предположим, что эксперимент повторяется n раз в неизменных условиях (т.е. вероятность Р(А)=р не изменяется при повторении экспериментов). Тогда относительная частота появление события А при n -> ∞ сходится по вероятности к р:

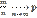, или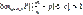

где n – общее число исходов,

m – число благоприятных исходов,

p – вероятность появления случ. величины.

Док-во:

Пусть 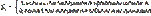Причем P[X_i=1]=p , а P[X_i=0]=q.

Вычислим математическое ожидание случайной величины X_i:

M[Xi] = 1*p + 0*q = p

И математическое ожидание их среднего арифметического:

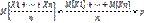
Случайные величины X_i , i=1…n по условию взаимно независимы, а их среднее арифметическое есть относительная частота появления события А в середине n экспериментов

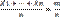
Теорема Бернулли дает математическое обоснование экспериментальным результатам, в которых наблюдается устойчивость частот при увеличении числа экспериментов.

Устойчивость среднего арифметического можно объяснить тем, что случайное отклонения от среднего, неизбежные в каждом отдельном результате, в массе однородных результатов взаимно поглощаются, нивелируются, выравниваются. Вследствие этого средний результат фактически перестает быть случайным и может быть предсказан достаточно точно.

№20. Центральная предельная теорема. Теорема Муавра-Лапласа. Асимптотическое распределение среднего арифметического случайных величин.

Центральная предельная теорема.
Одна из формулировок: Пусть X1…Xn… - независимые и одинаково распределенные случайные величины с мат.ожиданием m и дисперсией σ². Рассмотрим величину X=X1+…+Xn, при n->∞ функция распределения случайной величины

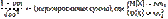
имеет нормальное распределение N(0,1) и равномерно по х сходится к функции распределения стандартного нормального закона Φ(х), где

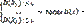
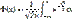
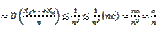Формулировка Ляпунова Пусть X1…Xn… - независимые и одинаково распределенные случайные величины с мат.ожиданием m и дисперсией σ².

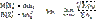
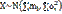
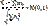
Следствия ЦПТ.