Решение простейших тригонометрических уравнений
I. Тригонометрические функции числового аргумента
Синус, косинус, тангенс и котангенс
1. Радианная мера. Угол в 1 радиан – это такой центральный угол, длина дуги которого равна радиусу окружности.
Радианная и градусная меры связаны зависимостью 180°=π радиан; угол в n° равен π n
180радиан.

 А
А

 с
с
b
 | |||
 | |||
С a В
Основные тригонометрические функции острого угла 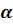 :
:

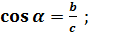 sin a =
sin a =  ; tg a =
; tg a =  ; ctg a =
; ctg a =  .
.
Основные формулы тригонометрии
Основные тригонометрические тождества:
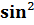
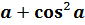 = 1;
= 1;
tg a = 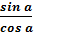 ctg a =
ctg a = 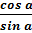 ;
;
tg a ctg a = 1;
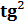 a + 1 =
a + 1 = 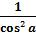 ;
;
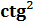 a + 1 =
a + 1 = 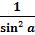 .
.
Формулы сложения:
cos(α – ß)= cosαcosß+ sinαsinß;
cos(α + ß)= cosαcosß - sinαsinß;
sin(α – ß)= sinαcosß- cosαsinß;
sin(α + ß)= sinαcosß + cosαsinß;
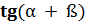 =
= 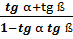 ;
;
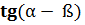 =
= 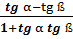 .
.

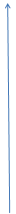
y 
 y
y
 |
x x
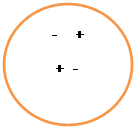
Знаки синуса Знаки косинуса
 y
y
 |
 x
x
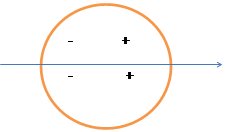
Знаки тангенса и котангенса
Формулы суммы и разности синусов (косинусов):

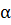 + sin
+ sin 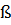 = 2 sin
= 2 sin 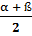 cos
cos 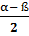 ;
;
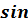
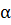 - sin
- sin 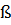 = 2 sin
= 2 sin 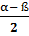 cos
cos 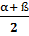 ;
;
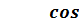
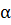 + cos
+ cos 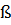 = 2 cos
= 2 cos 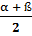 cos
cos 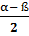 ;
;
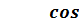
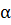 - cos
- cos 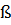 = - 2 sin
= - 2 sin 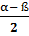 sin
sin 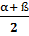 .
.
Формулы двойного аргумента:
sin 2 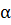 = 2 sin
= 2 sin 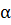 cos
cos 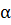 ;
;
cos 2 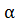 =
= 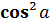 -
- 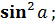
cos 2 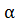 =
= 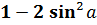 ;
;
cos 2 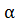 =
= 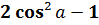 ;
;
tg 2 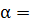
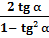 .
.
Формулы половинного аргумента:
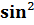
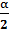 = sin
= sin 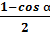 ;
;
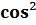
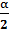 =
= 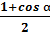 .
.
Упражнения.
1.Найдите значения других трех основных тригонометрических функций, если:
а) sin a = 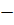 0,8
0,8  <a <
<a < 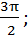
б) cos a = 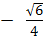
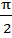 <a <
<a < 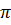 ;
;
в) sin a = 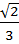 0 <a <
0 <a < 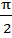 ;
;
г) cos a = 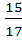
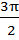 <a <
<a < 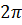 .
.
2.Упростите выражение:
а) 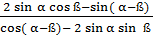 ;
;
б) 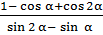 ;
;
в) 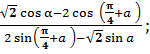
г) 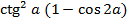 +
+ 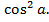
3.Докажите тождества:
a) 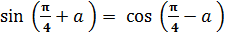 ;
;
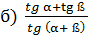 +
+ 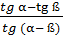 =2.
=2.
II. Решение тригонометрических уравнений и неравенств
Арксинус, арккосинус и арктангенс
Арксинусом числа а называется такое число из отрезка [ 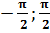 ], синус которого равен а.
], синус которого равен а.
Пример. Найдём аrcsin
аrcsin 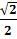 =
= 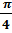 , так как sin
, так как sin 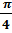 =
= 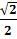 и
и 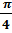 € [
€ [ 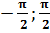 ].
].
Арккосинусом числа а называется такое число из отрезка [0 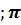 ], косинус которого равен а.
], косинус которого равен а.
Пример. arccos 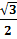 =
= 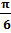 , так какcos
, так какcos 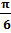 =
= 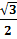 и
и 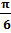 € [0
€ [0 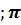 ].
].
Арктангенсом числа а называется такое число из интервала 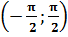 , тангенс которого равен а.
, тангенс которого равен а.
Пример. arctg 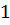 =
= 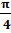 , так какtg
, так какtg 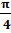 =1 и
=1 и 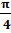 €
€ 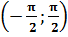
Арккотангенсом числа а называется такое число из интервала [0 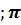 ], котангенс которого равен а.
], котангенс которого равен а.
Пример. arcctg 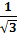 =
= 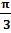 , так какctg
, так какctg 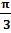 =
= 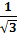 и
и 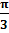 € [0
€ [0 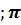 ]
]
Упражнения.
4.Найдите значения выражений:
4.1. а) arcsin 0 + arccos 0;
б) arcsin 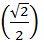 + arccos
+ arccos  ;
;
в) arcsin 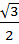 + arccos
+ arccos 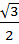 ;
;
г) arcsin ( 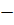 1) + arccos
1) + arccos 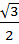 .
.
4.2. а) arccos ( 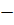 0,5) + arcsin (
0,5) + arcsin ( 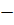 0,5);
0,5);
б) arccos 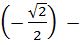 arcsin (
arcsin ( 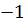 );
);
в) arccos 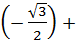 arcsin
arcsin 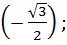
г) arccos 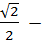 arcsin
arcsin 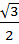 .
.
4.3. а) arctg 1 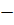 arctg
arctg 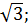
б) arctg 1 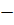 arctg (
arctg ( 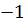 );
);
в) arctg 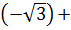 + arctg 0;
+ arctg 0;
г) arctg 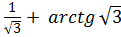 .
.
Решение простейших тригонометрических уравнений
Уравнение cos t = a (1)
(Если 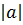 > 1, то уравнение не имеет решений)
> 1, то уравнение не имеет решений)
Формула корней уравнения (1): t = ± arccos a + 2 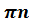 , n€ Z (2)
, n€ Z (2)
(Этой формулой можно пользоваться только при 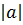 ≤ 1)
≤ 1)
Особая форма записи решений уравнений (1) принята также для a = 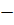 1 и a = 0:
1 и a = 0:
cos t = 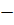 1при t =
1при t = 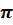 + 2
+ 2 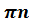 , n€ Z
, n€ Z
cos t = 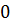 при t =
при t = 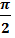 +
+ 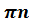 , n€ Z
, n€ Z
Пример 1. Решим уравнение cos x = 
По формуле (2) x = ± arccos  + 2
+ 2 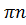 , n € Z
, n € Z
Уравнение sin t = a (3)
(не имеет решений при 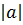 > 1, так как
> 1, так как 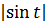 ≤ 1 для любого t)
≤ 1 для любого t)
Решения уравнения (3) удобно записывать не двумя, а одной формулой: \
t = (– 1)ᵏ 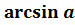 +
+ 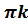 , k€ Z(4)
, k€ Z(4)
sin t = 1
t = 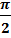 +2
+2 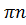 , n € Z.
, n € Z.
При а = 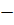 1 и а = 0 принята следующая запись решений:
1 и а = 0 принята следующая запись решений:
sin t = 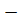 1, если t=
1, если t= 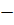
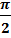 + 2
+ 2 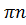 , n € Z.
, n € Z.
sin t =0, еслиt = 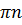 , n € Z.
, n € Z.
Пример 2. Решим уравнение: sin x = 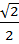 . По формуле (4)
. По формуле (4)
х = (– 1)ᵏ arcsin 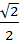 +
+ 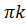 , k € Z, т.е.
, k € Z, т.е.
х=(– 1)ᵏ 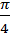 +
+ 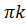 , k € Z.
, k € Z.
Уравнение tg t = a (5)
t = arctg a + 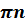 , n € Z. (6)
, n € Z. (6)
Пример 3. Решим уравнение: tg х = 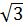 . По формуле (6) находим решение
. По формуле (6) находим решение
х = 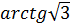 +
+ 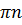 , n € Z , а так как
, n € Z , а так как 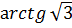 =
=  , приходим к окончательному ответу:
, приходим к окончательному ответу:
x = 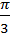 +
+ 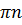 , n € Z.
, n € Z.
Упражнения.
5.Решите уравнения:
а) sin 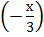 =
= 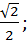
б) tg ( 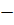 4x)
4x)  =
= 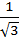 ;
;
в) cos ( 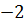 x) =
x) = 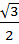 ;
;
г) ctg 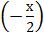 = 1.
= 1.
