В соответствии с (1) записываем условие задачи в виде

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.

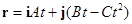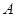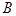1. Известен закон движения материальной точки: , где , и 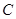– положительные постоянные величины. Получить уравнение траекто­рии. Найти зависимость от времени модуля скорости, модуля ускорения, нор­мального ускорения, тангенциального ускорения, радиуса кривизны траек­то­рии и угла между векторами скорости и ускорения.

Решение:

В соответствии с (1) записываем условие задачи в виде

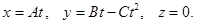
Выражаем время 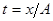и подставляем в выражение 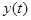, написанное выше. Получается уравнение траектории

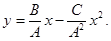
Это уравнение параболы, пересекающей ось 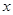в точке 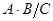(см. рис. 8), кото­рая сразу находится из условия .

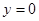Проекции вектора скорости на ос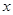и и 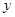находятся в соответствии с (3):

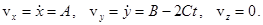
Модуль скорости согласно (4)

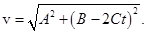
Ускорение в соответствии с (7) имеет одну компоненту

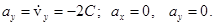
Таким образом, ускорение оказывается постоянным по величине и направлен­ным против оси 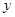. Его величина (8)

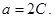
Угол 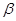между векторами скоро­сти 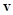и ускорения 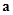можно найти из определе­ния скалярного произведения 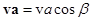и известного соотношения :

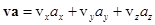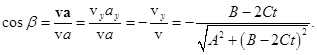
Тангенциальное ускорение (13)

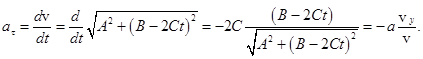
Нормальное ускорение по теореме Пифагора (12)

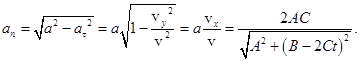
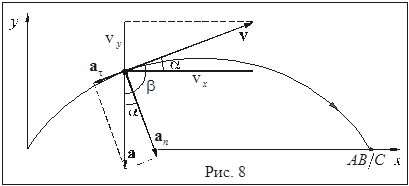
Полученные соотношения могут быть проиллюстрированы рисунком 8, который сам по себе достаточен для нахождения тангенциального и нормаль­ного ускорений. Действительно, 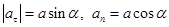, в то время как 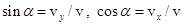, то есть

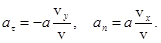
При движении «вверх», когда 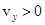, скорость 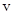уменьшается и 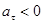; когда 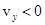, скорость увеличивается и 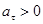. Таким образом, при получении танген­циального ускорения 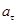можно уклониться от выполнения дифференцирования модуля скорости. С помощью рис. 8 можно найти и угол 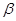между скоро­стью и ускорением: ,

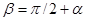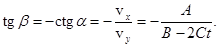
Наконец, по формуле (14) найдем радиус кривизны траектории:

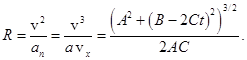
2. Диск радиусом 10 см вращается с угловым ускорением, равным 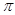рад/с². Сколько оборотов сделает диск при изменении частоты вращения от 2.0 оборотов в секунду до 4.0 оборотов в секунду? Найти время 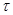, в течение кото­рого это произойдет. Определить нормальное и тангенциальное ускорения точек на окружности диска в момент времени 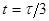. Определить угол между векто­рами скорости и ускорения в тот момент времени, когда диск вращался с часто­той 0.5 оборотов в секунду.

Решение:

Так как угловое ускорение постоянно, используем формулы равноуско­ренного вращения (21) – (22). Первое соотношение в (21) с учетом (24) сразу дает искомое время :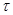

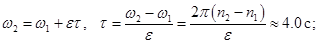
использованы данные условия задачи 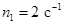, 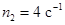. Полученное время 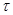можно просто под­ста­вить во второе соотношение (21) для нахождения угла по­ворота 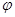, а с уче­том (23) – и числа оборотов :

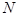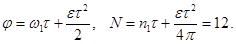
Правильнее будет подставить полученное выше выражение 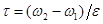в приведенную зависимость 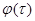, исключив время 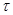и выразив ответ через дан­ные условия задачи. В результате этой процедуры получим формулу (22):

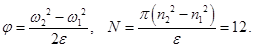
Тангенциальное ускорение согласно (19) оказывается постоянным

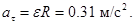
Для определения нормального ускорения по формуле (20) следует найти угло­вую скорость 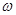в момент времени 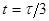с помощью (21):

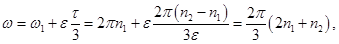
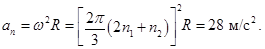
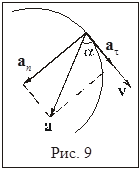
Угол 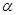между векторами скорости 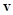и ускорения 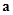можно найти, исполь­зуя векторы 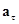и 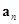. Тангенциальное ускорение 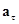направлено по касательной к окружности, т.е. так же, как и скорость 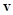. Поэтому (см. рис. 9)

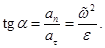
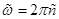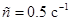Подставляя сюда , где и 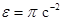, получаем

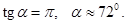
3. К пружинным весам подвешен легкий блок. Через него переброшена не­весомая нерастяжимая нить, к концам которой прикреплены два одинаковых груза массами по 5.0 кг. После того, как на один из грузов был поставлен пере­грузок массой 1.0 кг, система пришла в движение. Определить: 1) ускорение тел; 2) силу давления перегрузка на груз; 3) натяжение нити; 4) показание пру­жин­ных весов. Трение отсутствует.

Решение:

Данная в условии задачи система состоит, по крайней мере, из трех тел (см. рис. 10), поэтому необходимо написать три уравнения движения (для каждого из этих тел):

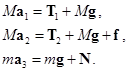
Если объединить два тела и справа в одно 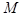+ 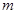, потеряем запрашивае­мую информацию о силе давления 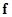перегрузка 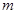на груз 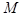. Согласно треть­ему закону Ньютона, сила реакции опоры 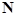, действующая со стороны груза на перегрузок, по величине равна силе давления :

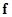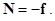
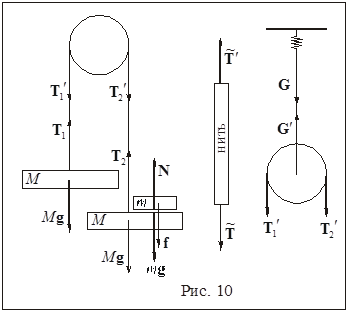
Нерастяжимость нити означает равенство по величине смещений, следова­тельно, и ускорений левого и правого грузов: 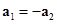. Правый груз и перегру­зок движутся вместе: 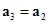. Поэтому ускорения всех трех тел будем считать одинаковыми по величине:

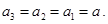
Так как масса нити равна нулю, то

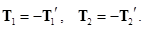
Это следует из уравнения движения нити, массу которой можно считать равной нулю,

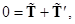
(см. рис. 10) и третьего закона Ньютона 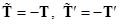. Так как масса блока равна нулю и отсутствует трение,

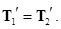
Таким образом, упрощающие предположения, зафиксированные в условии за­дачи, приводят к тому, что силу натяжения нити везде можно считать одинако­вой по величине:

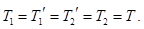
Далее спроектируем уравнения движения наших тел на произвольно вы­бранные вертикальные оси, например, левого – на ось, направленную вверх, правых – на ось, направленную вниз (можно и по-другому, результат будет тот же):

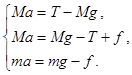
Теперь в системе трех уравнений три неизвестных: 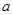, 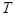и 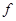. Решая эту сис­тему, получим

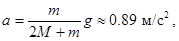
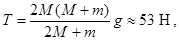
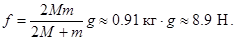
Обратите внимание на то, что вес перегрузка, равный силе 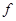по определению веса тела, меньше силы тяжести (0.91<1).

Осталось найти показания весов, к которым подвешен блок. Так как ось его неподвижна (к тому же он невесом), второй закон Ньютона для блока сводится к равенству нулю суммы всех действующих на него сил:

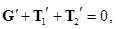
то есть 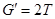. Наконец, сила 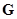, действующая на подвес, равная весу системы по определению веса,

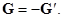
Чтобы это доказать, надо, как и для нити, рассмотреть участок системы от блока до пружины и использовать неподвижность этого участка. Поэтому показание пружинных весов, равное весу системы,

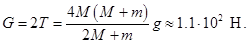
Обратите внимание на то, что вес системы отнюдь не равняется массе системы, умноженной на ускорение свободного падения:

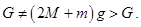
4. Найти период вращения маятника, совершающего круговые движения в горизонтальной плоскости (рис. 11). Длина нити равна 1м. Угол, образуемый нитью с вертикалью, равен 30⁰.

Решение:

Напишем уравнение движения груза на конце нити:

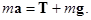
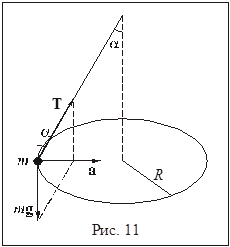
где 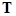– сила натяжения нити. Так как груз совершает равномерное движение по окружности, векторная сумма действующих на него сил направлена в центр этой окружности и равна массе груза 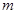, умноженной на его ускорение 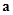, равное центростремительному (35):

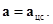
Значит, проекция суммы сил на вертикальную ось равна нулю (проекция 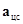на эту ось равна нулю):

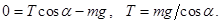
Проекция уравнения движения на другую, горизонтальную ось,

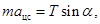
с учетом известного выражения (34) 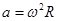и только что найденной силы натя­жения нити, дает величину угловой скорости кругового движения

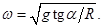
Используем связь радиуса окружности 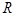с данной в условии длиной нити 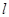: 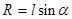. В результате находим угловую скорость

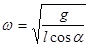
и период вращения

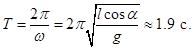
Для малых углов 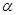, когда 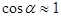, период вращения такого маятника совпа­дает с периодом его свободных колебаний.

5.Лодка неподвижно стоит в озере. На корме и на носу лодки на рас­стоянии 5м друг от друга сидят рыболовы. Масса лодки 50кг, массы рыболовов 60кг и 90кг. Рыболовы меняются местами. На какое расстояние переместится лодка относительно дна озера? Сопротивлением воды пренебречь.

Решение:

Решение этой задачи дает закон сохранения импульса (44) – (44’). На систему тел «рыбаки – лодка» действуют внешние вертикальные силы тяжести и реакции опоры (воды), проекция которых на горизонтальное направление равна нулю. Поэтому (см. (44’’)) сохраняется горизонтальная проекция им­пульса системы, которая равна нулю, так как вначале лодка стояла в воде не­подвижно. Это означает (см.(44’’)), что равна нулю и горизонтальная проекция скорости центра масс системы: как бы не передвигались рыбаки по лодке, центр масс системы не сдвинется относительно дна озера в горизонтальном направле­нии. Положение центра масс системы трех тел определяется формулой (42`)

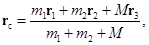
или, в проекции на произвольную ось ,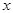

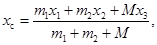
где 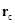, 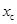– радиус-вектор и координата центра масс системы. В нашей задаче 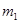, , 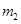, , 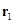, 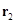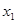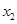– массы, радиус-векторы и координаты рыбаков, 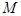– масса лодк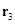и, и 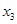– радиус-вектор и координата её центра масс.

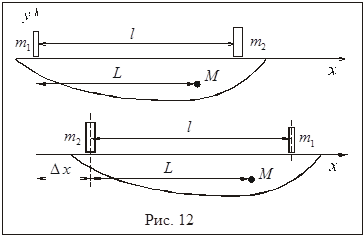
Выберем ось 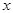горизонтальной с началом в месте расположения, ска­жем, первого рыболова до его перемещения (рис. 12). Учитывая, что 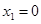, полу­чаем

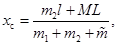
где 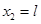– расстояние между рыбаками, 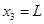– расстояние от первого ры­бака до центра масс лодки (см. рис. 12). Последнее расстояние в условии задачи не задавалось и должно исчезнуть в конечной расчетной формуле.

Теперь рыбаки поменялись местами, лодка передвинулась на 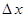, а центр масс системы остался на прежнем месте:

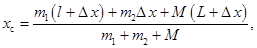
то есть

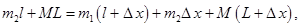
откуда

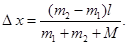
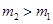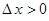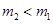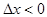Если , то и лодка передвигается вправо (как на рисунке), если , то и лодка передвигается влево на такое же расстояние 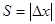. В нашей задаче .

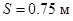6. Два шара подвешены на нитях одинаковой длины 90см так, что они соприкасаются. Массы шаров 100г и 200г. Меньший шар отклоняют на угол 90⁰ и отпускают. На какую высоту поднимутся шары после центрального абсо­лютно упругого соударения?

Решение:

Эта задача решается с помощью законов сохранения энергии и им­пульса. На движущийся вниз первый шар действует потенциальная сила тяже­сти, и его энергия, равная сумме кинетической и потенциальной 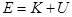, сохраняется. Сила натяжения нити перпендикулярна к скорости шара и работы не совершает; трение не учитываем. Вверху равна нулю кинетическая энергия. Внизу, на подлете ко второму шару, равна нулю его потенциальная энергия. Таким образом, потенциальная энергия переходит в кинетическую:

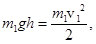
где 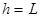– длина нити, 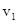– скорость первого шара непосредственно перед уда­ром,

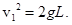
При абсолютно упругом ударе первого шара о второй сохраняется и им­пульс системы этих двух тел, и энергия:

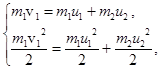
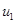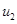где и – горизонтальные проекции скоростей шаров сразу после удара. Най­дем эти скорости. Для этого перепишем систему законов сохранения в виде:

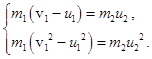
Поделив второе уравнение на первое, получим

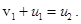
Подставляя это в закон сохранения импульса, получаем скорости шаров после удара:

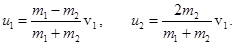
При 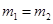первый шар останавливается ( 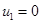), а скорость второго после удара равна скорости первого до удара ( 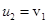). Так как в нашей задаче 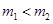, то 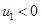, то есть первый (меньший) шар отскакивает назад.

Высоту, на которую поднимется шар после удара, найдем опять из закона со­хранения энергии

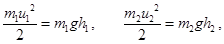
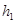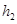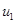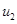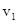где и – высоты подъемов первого и второго шара. Подставляя сюда найден­ные выражения для , и , получаем результат:

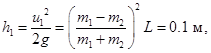
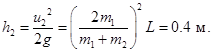
7. На однородный цилиндр намотана гибкая нерастяжимая лента длиной 1 м, масса которой много меньше массы цилиндра. Свободный конец ленты за­крепили, а цилиндр отпустили. Найти время разматывания ленты.

Решение:

Решим эту задачу двумя способами.

Способ 1.

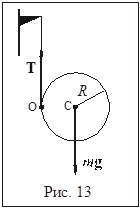
Цилиндр совершает вращательное движение относительно оси, проходя­щей через его центр масс (точка C на рис. 13) и поступательное движение этой точки вниз. Уравнением поступательного движения является второй закон Нью­тона. Запишем его в проекции на ось, направленную вертикально вниз,

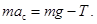(62)

Уравнение вращательного движения (50):

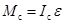
Здесь 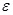угловое ускорение цилиндра, 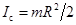- его момент инерции относи­тельно оси, проходящей через центр масс (57), 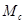– величина момента силы натяжения ленты 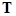относительно точки С,

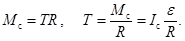(63)

Момент силы тяжести 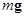относительно этой точки равен нулю, т.к. равно нулю плечо этой силы.

Подставляя T из (63) в (62), получаем

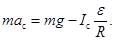
Ускорение 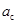точки С равно по величине тангенциальному ускорению поверх­но­сти цилиндра относительно точки С, которое в свою очередь равно 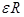(19),

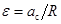
Подставляя это в предыдущее уравнение

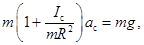
находим ускорение оси цилиндра

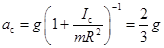
и время 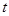прохождения пути, равного длине ленты :

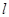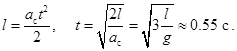
Способ 2.

За время 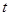лента разматывается на длину

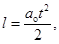
где 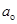– ускорение перемещения точки О (ускорение разматывания), .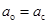