Модификация основной постановки. В данном разделе рассмотрим модификации общей задачи многошаговой оптимизации и соответствующие варианты алгоритма динамического программирования
В данном разделе рассмотрим модификации общей задачи многошаговой оптимизации и соответствующие варианты алгоритма динамического программирования.
1. В ряде случаев кроме начального состояния s0 и числа шагов N задаётся финальное со-стояние s*. Это означает, что φ(sN−1,vN) =s*. При переходе к графу это означает, что искомый максимальный путь должен кончаться в соответствующей состоянию s* вершине x*. Модифи-кация алгоритма в этом случае практически очевидна. На итерации 1 в правом столбце для каж-дой вершины x слева пишется вес дуги (x, x*), а справа – номер x (напомним, что все вершины графа занумерованы числами 1, 2, …, n). Начиная с итерации 2, алгоритм полностью совпадает с рассмотренным в примере 1 (см. таблицы 1.2 – 1.6).
2. Иногда требуется найти не оптимальный путь длины N, а оптимальный путь длины не более N, с заданной или не заданной конечной вершиной. В этих случаях применяются точно те же самые алгоритмы. Ведь суть динамического программирования как раз в том, что последо-вательно находятся оптимальные пути из всех вершин длины 1, длины 2, …, длины N. После этого надо просмотреть числа из строки, соответствующей начальному состоянию, и выбрать из них максимальное или минимальное. В примере 1 путём с максимальным весом среди всех путей длины не более 6-и с началом в вершине 1 оказывается путь длины 6 (см. таблицу 1.6). А в примере 2 на минимизацию оптимальным при тех же условиях оказывается не путь длины 6, вес которого равен –3, а путь длины 1, вес которого равен –4. Естественно, это может случиться только в случае, когда имеются дуги с весами разных знаков. В противном случае вес любого пути при добавлении дуги увеличивается (если веса всех дуг положительны) или уменьшается (если веса всех дуг отрицательны). В этих случаях такие постановки не имеют смысла.
3. В некоторых ситуациях естественно связывать доходы не с переходом из состояния в состояние, а с самими состояниями. Однако эту ситуацию легко свести к предыдущей, положив в построенном графе вес каждой дуги равным доходу от вершины, являющейся концом данной дуги. Тогда вес любого пути станет равным суммарному весу всех его вершин, кроме началь-ной. Поскольку этот вес один и тот же для всех путей с фиксированным начальным состоянием, это не влияет на определение оптимального пути.
4. Если не задавать число шагов N в многошаговом процессе, то тем самым не будет зада-ваться и число дуг (т.е. длина пути) в соответствующем графе. Понятно, что если отсутствуют какие бы то ни было требования к графу и∕ или к виду искомых путей, то задача оптимизации просто может не иметь решения. В частности, если в графе есть цикл положительной длины, а пути могут содержать циклы, понятно, что вес пути при многократном прохождении такого по-ложительного цикла может быть сделан сколь угодно большим. В то же время ограничения на вид пути (например, запрет на повторяющиеся вершины или дуги) просто «не встраиваются» в алгоритм динамического программирования (в том смысле, что найденные при ограничениях пути не обязаны быть оптимальными). Наиболее естественно в этих случаях выглядят такие ус-ловия на граф, при котором длины любых путей будут ограниченными (напомним, что речь в этой главе идёт только об ориентированных графах и путях). Именно такие постановки рассмотрены в следующем разделе.
3.1. Ацикличные задачи многошаговой оптимизации.Под такими задачами будут по-ниматься задачи, в которых под действием любого многошагового управления никогда нельзя вернуться в начальное состояние. Такие задачи часто связаны с тем, что время, которое всегда течёт в одну сторону, является одним из параметров, определяющих состояние системы. Соот-ветствующий граф будет ацикличным. В силу утверждения 5.8 множество вершин графа распа-дается на подмножества (которые можно называть слоями), такие, что любая дуга ведёт из слоя с бóльшим номером в слой с мéньшим номером. Для упрощения обозначений будем считать, что 0-ой слой состоит из единственной вершины x* и что рассматриваются пути, оканчивающи-еся в этой вершине. Обычно такая вершина соответствует окончанию рассматриваемого много-шагового процесса. Напомним, что число шагов Nв данной модификации не задаётся.
Обозначим через W(x) вес оптимального пути, ведущего из вершины x в вершину x*. Ос-новное уравнение Беллмана можно записать в виде
W(x) = maxy{w(x, y) + W(y)}, (8)
где максимум берётся по всем вершинам y, в которые ведёт дуга из вершины x. Учитывая, что все дуги ведут в слои с мéньшими номерами, знание оптимальных путей для всех вершин из слоёв Vr, Vr−1, …, V1 в вершину x*, образующую слойV0 позволяет по формуле (8) легко найти оптимальные пути для всех вершин из слоя Vr+1. Можно сказать, что в отличие от общего слу-чая, переход здесь делается не по шагам для всех вершин, а по слоям, которых обычно значи-тельно меньше, чем вершин. Соответственно, таблицы, заполнение которых позволяет найти оптимальный путь, также меняются и становятся значительно более обозримыми.
3.1.1. Сетевое планирование.В этом разделе мы остановимся на одном важном классе прикладных задач – так называемых задачах сетевого планирования. Оно используется при про-ведении крупных разработок, включающих в себя выполнение целого комплекса взаимосвязан-ных работ (например, строительство, разработка новых технических систем и изделий, проведе-ние ремонта и реконструкции предприятий и агрегатов и т.п.). Сетевые методы основаны на на-глядном представлении выполняемого комплекса работ в виде ориентированного графа, дуги которого изображают выполняемые работы, а вершины – события, представляющие собой за-вершение одних работ и начало других. Последовательность дуг в таком графе определяет по-рядок, в котором выполняются работы.
На рис.2 приведён пример сетевого графика, на котором показаны работы, необходимые для изготовления некоторого прибора. Сетевой график даёт наглядное представление о порядке выполнения работ, что даёт возможность наиболее рационально распорядиться имеющимися ресурсами. Сам граф отражает ограничения, связанные с выполнением данного комплекса ра-бот. Ясно, что производство деталей может быть начато только после подготовки чертежей и т.д.
Итак, у нас уже есть сетевой график. Более того, будем считать, что уже определены (на-пример, при помощи экспертов) длительности отдельных работ. Возникает вопрос – чему равна длительность выполнения всего комплекса? Этот вопрос не является простым, поскольку в ре-альных ситуациях число дуг и вершин в сетевом графике может достигать нескольких сотен. Для ответа на поставленный вопрос возможно использование динамического программирова-ния.
| контрольные испытания |
| производство деталей |
| отгрузка |
| сборка |
| поставка деталей |
| Выдача заказов на детали |
| проектирование |
| подготовка и составление инструкции |
| подготовка чертежей |
Рис.2
Проведём дальнейшую формализацию задачи. Естественно считать, что графG, описыва-ющий последовательность работ, является ацикличным, поскольку наличие цикла означает, на-пример, что работа Б должна выполняться после окончания работы A, работа В – после работы Б, а работа А – после работы В. Можно считать также, что в графе G есть ровно одна вершина, в которую не входит ни одна дуга, и ровно одна вершина, из которой не выходит ни одна дуга. Эти вершины соответствуют началу и завершению всего комплекса работ. Каждой дуге графа приписано положительное (не обязательно целое) число (длина дуги), которое интерпретирует-ся как длительность операции (работы), условно представляемой данной дугой.
Рассмотрим любой ориентированный путь Р из начальной вершины x0 в конечную верши-ну x*. Рассмотрим сумму длин дуг, образующих путь Р, и обозначим её через Т(Р). Так как операции, соответствующие дугам одного и того же пути, могут выполняться только после-довательно (по построению сетевого графика), то общая длительность выполнения всего комп-лекса не меньше, чем Т(Р). Поскольку в качестве Р был взят произвольный путь, то
Тоб ≥ 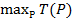
Таким образом, возникает задача поиска пути максимальной длины (такой путь в сетевом графике называется критическим). Эта задача в общем виде рассматривалась в начале раздела 3.1. Начальная вершина x0 и конечная вершина x* – это входная и выходная вершины сетевого графика. Число дуг в пути не фиксируется. Основная идея заключается в разделении множества вершин графа на слои. При этом начальный слой состоит из единственной выходной вершины, а последний слой состоит из единственной входной вершины. Основой для перехода от слоя к слоя служит уравнение Беллмана (8).
Пример 3. Рассмотрим сетевой график, показанный на рис. 3. Пунктирная линия не соот-ветствует никакой конкретной работе и её длина равна 0. Вводятся такие «псевдоработы» толь-ко для того, чтобы правильно отражать последовательность реальных работ. В рассматривае-мом случае включение псевдоработы Р означает, что работа З не может быть начата до оконча-ния работы В. Использование псевдоработ не меняет последовательности любых других опера-ций и не изменяет длины критического пути.
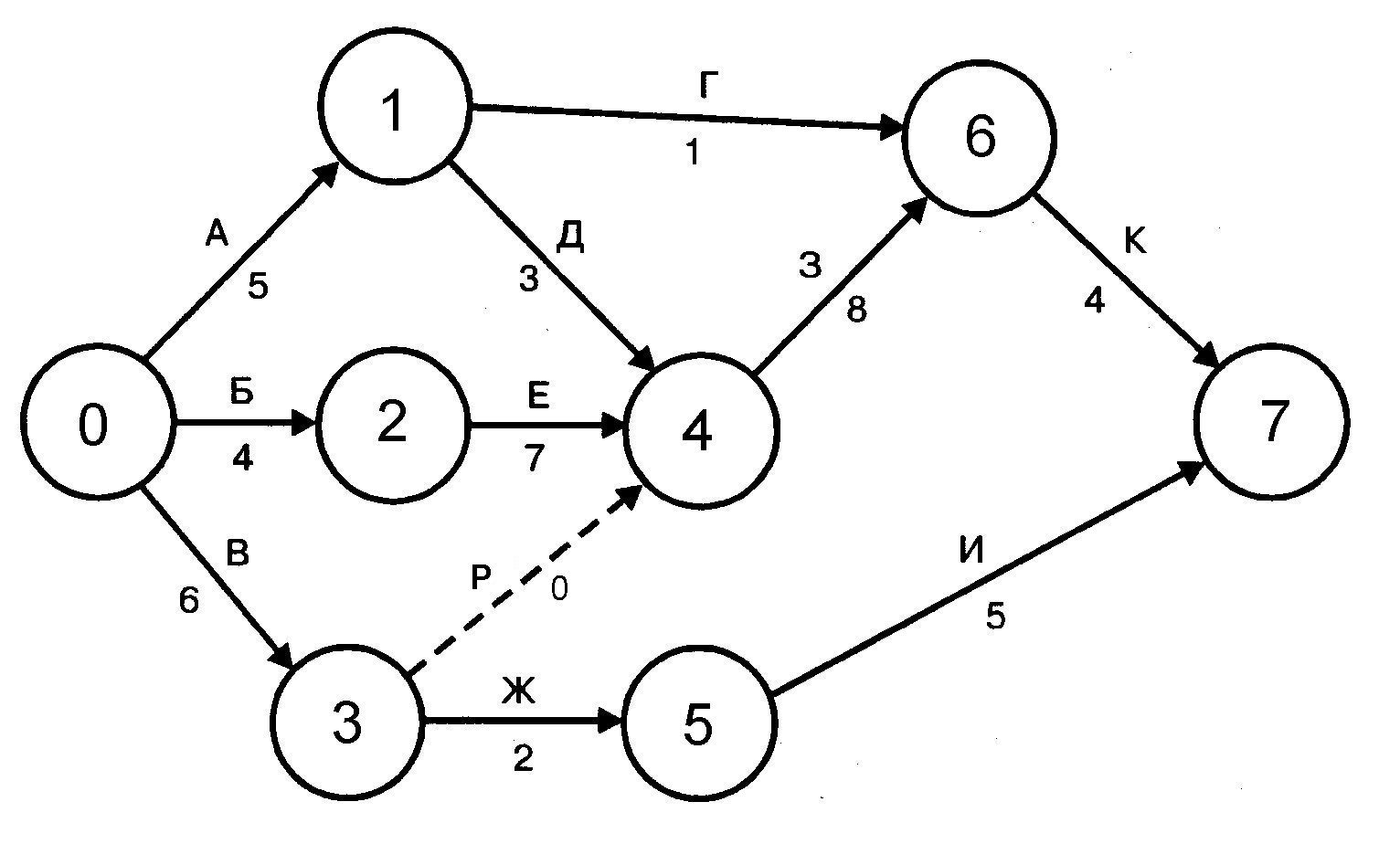
Рис.3. Пример сетевого графика
Построим разбиение множества вершин графа, показанного на рис.3, в соответствии с доказательством утверждения 5.8:
1. Положим G0 = G, V0={7}.
2. Удалим из графа G0 вершину 7 и ведущие в неё дуги И и К. Оставшийся граф G1 показан на рис.4а. В этом графе из вершин 5 и 6 не выходит дуг, и в соответствии с процедурой из упомянутого доказательства V1={5,6}.
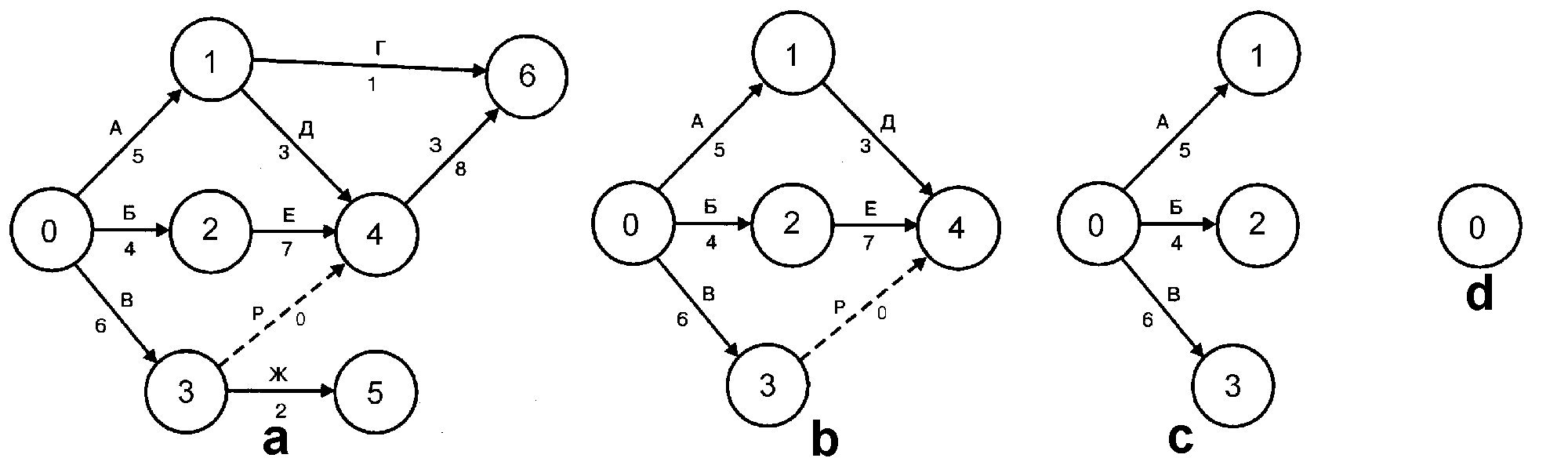
Рис.4
3. Удалим из графа G1 (см. рис.4а) вершины 5, 6 и ведущие в них дуги Ж, З и Г. Остав-шийся граф G2 показан на рис.4b. В этом графе из вершины 4 не выходит дуг, и в соответствии с той же процедурой V2={4}.
4. Удалим из графа G2 (см. рис.4b) вершину 4 и ведущие в неё дуги Р, Е и Д. Оставшийся граф G3 показан на рис.4с. В этом графе из вершин 1, 2, 3 не выходит дуг, и в соответствии с процедурой V3={1, 2, 3}.
5. Удалим из графа G3 (см. рис.4с) вершины 1, 2, 3 и ведущие в них дуги А, Б и В. Остав-шийся граф G4 показан на рис.4d. В этом графе имеется только одна вершина 0 и в соответствии с той же процедуройV4={0}.
6. Процедура окончена, поскольку других вершин больше нет. Построено следующее раз-биение:
V0={7}, V1={5, 6},V2= {4}, V3={1, 2, 3}, V4={0} (9)
и любая дуга ведёт из слоя с бóльшим номером в слой с мéньшим номером. Задача состоит в том, чтобы определить путь максимальной длины из вершины 0 в вершину 7.
Инициализация и итерация 1. Составим таблицу, столбцы которой соответствуют верши-нам заданного графа G. Расположим эти столбцы слева направо в соответствии с разбиением (9): сначала идёт столбец, соответствующий вершине 0, потом (в произвольном порядке) – столбцы, соответствующие вершинам 1, 2, 3 и т.д., вплоть до вершины 7. Число ячеек в каждом столбце равно числу дуг, выходящих из данной вершины, плюс одна строка (на следующую вершину в искомом максимальном пути).
Таблица 3.1. Нахождение критического пути. Инициализация и итерация 1
Каждая ячейка соответствует одной дуге, выходящей из вершины. В правую верхнюю клетку ячейки пишется номер вершины, в которую идёт дуга; в левую верхнюю – её длина. Так, из вершины выходят две дуги: в вершину 4 длины 0 (псевдоработа) и в вершину 5 длины 2. Эти данные полностью описывают исходный сетевой график и далее не меняются.
На итерации 1 определяются максимальные пути из вершин из 1-го слоя. По самой конструкции ясно, что такие пути совпадают с дугами, ведущими из этих вершин в конечную вершину 7. Длина максимального пути и следующая вершина на нём пишутся в нижние две клетки каждого столбца. Поэтому на итерации 1 туда просто копируются числа из верхних двух клеток.
Итерация 2. На итерации 2 определяются максимальные пути для вершин из слоя V2= {4}.
Таблица 3.2. Итерация 2
В левую нижнюю клетку из верхней ячейки столбца 4 пишутся сумма длины 8 (от вершины 4 до вершины 6) и длины 4 (максимальной длины от вершины 6 до конечной вершины 7, взятой из левой нижней клетки в столбце 6). В правую нижнюю клетку этой же ячейки пишется номер вершины 6. Поскольку других дуг, выходящих из вершины 4, нет, то эти же два числа копируются в нижнюю строчку столбца 4. Тем самым уже найден максимальный путь из вершины 4 в вершину 7: 4→6→7.
Итерация 3. На итерации 3 определяются максимальные пути для вершин из слоя V3= {1,2, 3}.
Таблица 3.3. Итерация 3
Начинаем для определённости с правого (из этого слоя) столбца 3. 1-ая сверху ячейка в этом столбце соответствует дуге (3,4) длины 0. В левую нижнюю клетку этой же ячейки запи-сываем сумму длины 0 и длины 12 из нижней строчки столбца 4 (максимальной длины пути из 4 в 7). Далее, в следующей сверху ячейке столбца 3 записываем сумму длины 2 дуги (3,5) и дли-ны 5 максимального пути из вершины 5 в вершину 7 (взятую из нижней строки столбца 5). Ко-пируем в нижнюю строку столбца 5 ту из двух полученных строк – (12,4) и (7,5) – в которой длина (1-ое число) больше. Поэтому копируем (12,4). Заметим, что именно здесь реализуется уравнение Беллмана (8).
Столбец 2 содержит только одну ячейку, которая соответствует дуге (2,4) длины 7. Запи-сываем в нижнюю половину этой ячейки длину 19 = 7+12 и вершину 4; ту же пару копируем в нижнюю строку.
Столбец 1 содержит две ячейки, соответствующие дугам (1,4) длины 3 и (1,6) длины 1. Записываем суммы и выбираем максимальную из них для записи в нижнюю строку.
Итерация 4. На итерации 4 определяются максимальные пути для вершин из последнего слоя V4= {0}. Столбец 1 содержит 3 ячейки, соответствующие дугам (0,1), (0,2) и (0,3). В верхнюю ячейку запишем длину 20 = 5 + 15 и номер 1.В следующую ячейку запишем сумму 23 = 4 + 19 и номер 2. В нижнюю ячейку запишем сумму 18 = 6 + 12 и номер 3. В нижнюю строку запишем пару с максимальной длтной 23.
На этом итерации закончены. Искомый путь выделен подсветкой в нижних строчках. Он таков: 0→2→4→6→7. Его длина равна 23.
Таблица 3.4. Итерация 4
■
Особенно простым алгоритм динамического программирования становится в случае, ког-да каждая дуга ведёт из слоя в слой с предыдущим номером, а число выходящих дуг всегда равно 2. Именно такой случай рассмотрен в следующем подразделе.
3.1.2. Задача о замене машины.В настоящем разделе приводится конкретный пример, иллюстрирующий введенные понятия и рассматриваемую модификацию алгоритма динами-ческого программирования. Одной из основных проблем индустрии является проблема замены старого парка машин новым, устаревших орудий современными устройствами. Оборудование со временем изнашивается как в буквальном смысле слова, так и «морально», т.е. устаревает по сравнению с более современным модернизированным оборудованием. Наступает момент, когда большие затраты на новое оборудование, убытки вследствие остановки производства и расходы на переподготовку кадров - всё это компенсируется увеличением производительности и умень-шением производственных затрат.
Содержательно задача о замене состоит в определении оптимальной политики модерниза-ции и замены оборудования, т.е. в определении последовательности замен, максимизирующей
суммарную прибыль.
Введем упрощающие предположения. Предположим, что у нас имеется только одна ма-шина, которая приносит ежегодно некоторый доход, требует определённого ухода и может быть в любой момент продана и заменена новой машиной, аналогичной старой, но более эф-фективной. Для определенности будем считать, что замена может быть осуществлена один раз в год (именно, в начале каждого года). Предполагается также, что доход, затраты на содержание и стоимость замены машины известным образом зависят от срока ее службы.
Рассмотрим процесс, длящийся 6 лет. Затраты на замену машины, доход и затраты на со-держание новых машин, появляющихся к началу каждого из этих 6 лет, в зависимости от воз-раста машины (т.е. числа полных лет, которые она уже проработала), приведены в таблице 4 (в условных единицах). Мы начинаем процесс, имея машину, называемую исходной, прослужив-шую уже 3 года; её характеристики представлены в таблице .
Общий (суммарный) доход равен сумме доходов, полученных на каждом году работы. До-ход за каждый год может быть получен из дохода (указанного в таблицах 4 и 5) путём вычи-тания затрат на содержание машины и (в случае замены в начале этого года) затрат на замену.
Таблица 4. Данные о новых машинах
Машина, новая в начале 1-го года
Машина, новая в начале 2-го года
| Машина, новая в начале 4-го года
Машина, новая в начале 5-го года
|
| Машина, новая в начале 3-го года
| Машина, новая в начале 6-го года
|
Таблица 5. Данные об исходной машине
| Возраст машины | ||||||
| Доход | ||||||
| Затраты на содержание | ||||||
| Затраты на замену |
Выбор оптимальной последовательности замен можно осуществить в результате примене-ния метода динамического программирования. Для этого, в соответствии с тем, что излагалось в этом разделе 3.1, надо определить:
множество S состояний;
множества Qs воздействий для всех sÎS;
функцию переходов φ(s,v);
функцию дохода ψ(s,v);
начальное состояние s0ÎS;
число шагов N.
Определим указанные параметры задачи.
1. Элементами множества S естественно считать пары вида (t,t) , где t- текущий год (t = 1, 2, ..., 6), t- возраст машины на начало года t. Обратим внимание на следующее. В последний (шестой) год есть пара (6,8) (она соответствует старой машине, у которой в начале 6-го года возраст 8 лет), есть пара (6,5) (она соответствует машине, новой в начале 1-го года, у которой в начале 6-го года возраст 5 лет), пара (6,4) (она соответствует машине, новой в начале 2-го года, у которой в начале 6-го года возраст 4 года) и т.д. Состояний (6,7) и (6,6) в множестве Sпросто нет! Точно также нет пар (5,6) и (5,5), (4,5) и (4,4) и т.д. Обратим внимание, что пар вида (t,0) также нет. В начале года у нас ещё нет новой машины, поэтому возраст имеющейся не меньше 1-го года. Если же мы приняли решение о покупке новой машины, то через год её возраст также будет не меньше 1-го года. Наконец, необходимо ввести «финальное» состояние (обозначим его через s*), соответствующее завершению процесса после окончания 6-го года.
2. Множество воздействий Qs для любого состояния sÎS, кроме состояния s*, состоит из двух элементов: С и Н (оставить старую машину еще на один год или заменить ее новой). Для состояния s* множество Qs пусто.
3. Функция переходов φ(s,v) определяется формулами
φ((t,t),С) = (t+1,t+1) (t = 1, ..., 5),
φ((t,t),Н) = (t+1,1) (t = 1, ..., 5),
φ((6,t),С) = φ((6,t),Н) = s*.
Действительно, если в начале года t решено оставить старую машину (v = С), то её возраст t через год увеличивается на 1; если же решено заменить машину новой (v = Н), то её возраст через год равен 1. Поскольку 6-й год является последним, то и соответствующее состояние сов-падает с s*.
4. Для определения функции доходов требуется использовать данные из таблиц 4 и 5. Вычислим (в качестве примера) ψ((5,3),С) и ψ((5,3),Н). Состояние (5,3) означает, что имеющая-ся на данный момент машина к началу 5-го года проработала 3 года. Но это означает, что она была новой в начале 2-го года. Из таблицы 3 для этой машины находим, что она (при возрасте 3 года) дает за год доход 110 при затратах 15, откуда ψ((5,3),С) = 110 - 15 = 95. Если принять решение Н (заменить машину новой), то расходы на её замену (из таблицы 3 для этой же маши-ны) составляют в начале 5-го года (т.е. 3-го года её работы) 110; новая же машина (новая в на-чале 5-го года) приносит в течение 1-го года своей работы (при возрасте 0) доход 150 при затратах 5. Таким образом, ψ((5,3),Н) = -110 +150 -5 = 35. Аналогично подсчитываются значе-ния этой же функции ψ((t,t),v) при всех состояниях (t,t) и воздействиях v. Эти данные собраны в таблице 6.
Таблица 6. Функция доходов
| (t,τ) | ψ((t,τ),C) | (t,τ) | ψ((t,τ),C) | (t,τ) | ψ((t,τ),H) | (t,τ) | ψ(t,τ),H) |
| (6,8) | −15 | (4,6) | −10 | (6,8) | −10 | (4,6) | −15 |
| (6,5) | (4,3) | (6,5) | (4,3) | ||||
| (6,4) | (4,2) | (6,4) | (4,2) | ||||
| (6,3) | (4,1) | (6,3) | (4,1) | ||||
| (6,2) | (3,5) | −5 | (6,2) | (3,5) | −15 | ||
| (6,1) | (3,2) | (6,1) | (3,2) | ||||
| (5,7) | −10 | (3,1) | (5,7) | −5 | (3,1) | ||
| (5,4) | (2,4) | (5,4) | (2,4) | −15 | |||
| (5,3) | (2,1) | (5,3) | (2,1) | ||||
| (5,2) | (1,3) | (5,2) | (1,3) | −10 | |||
| (5,1) | (5,1) |
5. Начальное состояние s0 = (1, 3) (по условию мы начинаем процесс при исходной машине, прослужившей 3 года).
6. Описанный процесс начинается в начале 1-го года, а заканчивается в начале 7-го года, т.е. сразу после окончания 6-го года. В каждом следующем состоянии (t,τ) 1-ая компонента t увеличивается на 1 независимо от выбранного управления С или Н. Поэтому любой из возмож-ных процессов состоит из 6 шагов, т.е. N = 6.
Приведём теперь разбиение всех состояний на слои (см. материал из раздела 3.1 до начала раздела 3.1.1. По построению, все состояния (t,τ), образующие один слой, содержат одну и ту же компоненту t. Итак:
S0 = s*; S1 = {(6,8), (6,5), (6,4), (6,3), (6,2), (6,1)}; S2 = {(5,7), (5,4), (5,3), (5,2), (5,1)};
S3 = {(4,6), (4,3), (4,2), (4,1)}; S4 = {(3,5), (3,2), (3,1)}; S5 = {(2,4), (2,1)};S6 = {(1,3)}.
Итерация 1. Образуем таблицу 7.1, в которую при инициализации занесём исходные дан-ные. Таблица содержит 12 столбцов с разным числом строк. На этот раз ячейки состоят из 4-ёх клеток. В левой верхней клетке записано состояние (t,t) , где t- текущий год (t = 1, 2, ..., 6), t-
Таблица 7.1. Инициализация и итерация 1
| (1,3) | (2,4) | (3,5) | −5 | (4,6) | −10 | (5,7) | −10 | (6,8) | −15 | s* | ||
| −10 | −15 | −15 | −15 | −5 | −10 Н | −10 | ||||||
| (2,1) | (3,2) | (4,3) | (5,4) | (6,5) | ||||||||
| 80 С | ||||||||||||
| (3,1) | (4,2) | (5,3) | (6,4) | |||||||||
| 90 С | ||||||||||||
| (4,1) | (5,2) | (6,3) | ||||||||||
| 95 С | ||||||||||||
| (5,1) | (6,2) | |||||||||||
| 115 С | ||||||||||||
| (6,1) | ||||||||||||
| 130 С |
возраст машины на начало года t. В верхней правой клетке записан доход за один год при вы-боре управления С (т.е. при продолжении работы на старой машине), в нижней правой клетке записан доход за один год при выборе управления Н (при покупке новой машины). Эти данные взяты из таблицы 6. Важной особенностью таблицы 7.1 является следующее: при t< 6 для каж-дого состояния (t,t) при выборе управления С следующим состоянием является то, которое за-писано в ячейке справа от (t,t); при выборе управления Н следующим состоянием является то, которое записано в нижней ячейке столбца справа от (t,t). При t = 6 следующим состоянием яв-ляется состояние s* (завершение процесса), независимо от выбора управления.
На итерации 1 в оставшуюся левую нижнюю клетку в 1-ом слое запишем наибольшее из двух чисел в правых клетках и букву С, если бóльшим оказалось верхнее число (букву Н, в противном случае). Таким образом, оптимальные действия для всех состояний из 1-го слоя (т.е в начале 6-го года) становятся известны. Во всех случаях, кроме одного – если машина раньше вообще не заменялась – выгоднее продолжать работать на имеющейся в этот момент машине. Если же она ни разу не менялась, лучше её заменить.
Итерация 2. Заполним оставшиеся пустыми клетки во 2-ом слое. В основе лежит уравне-ние Беллмана (8). В правую верхнюю клетку каждой ячейки из 2-го слоя таблицы 6.2 запишем сумму того, что там было, и числа из левой нижней клетки из ячейки справа. В соответствии с методом динамического программирования, это будет максимальный доход, если принять ре-шение С. В правую нижнюю клетку каждой ячейки из 2-го слоя таблицы 6.2 запишем сумму то-го, что там было, и числа из левой нижней клетки нижней ячейки из слоя справа. В соответст-вии с методом динамического программирования, это будет максимальный доход, если принять решение Н.
Теперь в остававшуюся до сих пор пустой левую нижнюю клетку каждой ячейки 2-го слоя запишем наибольшее из двух чисел в правых клетках этой же ячейки и букву С, если бóльшим оказалось верхнее число (букву Н, в противном случае). Таким образом, оптимальные действия для всех состояний из 2-го слоя (т.е в начале 5-го года) стали известными.
Таблица 7.2. Итерация 2
| (1,3) | (2,4) | (3,5) | −5 | (4,6) | −10 | (5,7) | −25 | (6,8) | −15 | s* | ||
| −10 | −15 | −15 | −15 | 125 Н | −10 Н | −10 | ||||||
| (2,1) | (3,2) | (4,3) | (5,4) | (6,5) | ||||||||
| 175 Н | 80 С | |||||||||||
| (3,1) | (4,2) | (5,3) | (6,4) | |||||||||
| 185 С | 90 С | |||||||||||
| (4,1) | (5,2) | (6,3) | ||||||||||
| 185 С | 95 С | |||||||||||
| (5,1) | (6,2) | |||||||||||
| 240 С | 115 С | |||||||||||
| (6,1) | ||||||||||||
| 130 С |
Итерация 3. Заполним оставшиеся пустыми клетки во 3-ьем слое. Поступаем также, как на итерации 2. В правую верхнюю клетку каждой ячейки из 3-го слоя таблицы 7.3 запишем сумму того, что там было, и числа из левой нижней клетки из ячейки справа. В правую нижнюю клетку каждой ячейки из 3-го слоя таблицы 7.3 запишем сумму того, что там было, и числа из левой нижней клетки нижней ячейки из слоя справа. В остававшуюся до сих пор пустой левую левую нижнюю клетку каждой ячейки 3-го слоя запишем наибольшее из двух чисел в правых клетках этой же ячейки и букву С, если бóльшим оказалось верхнее число (букву Н, в против-ном случае). Таким образом, оптимальные действия для всех состояний из 3-го слоя (т.е в начале 4-го года) стали известными.
Таблица 7.3. Итерация 3
| (1,3) | (2,4) | (3,5) | −5 | (4,6) | −35 | (5,7) | −25 | (6,8) | −15 | s* | ||
| −10 | −15 | −15 | 225 Н | 125 Н | −10 Н | −10 | ||||||
| (2,1) | (3,2) | (4,3) | (5,4) | (6,5) | ||||||||
| 280 Н | 175 Н | 80 С | ||||||||||
| (3,1) | (4,2) | (5,3) | (6,4) | |||||||||
| 285 С | 185 С | 90 С | ||||||||||
| (4,1) | (5,2) | (6,3) | ||||||||||
| 300 С | 185 С | 95 С | ||||||||||
| (5,1) | (6,2) | |||||||||||
| 240 С | 115 С | |||||||||||
| (6,1) | ||||||||||||
| 130 С |
Далее аналогично выполняются итерации 4, 5 и 6.
Итерация 4:
Таблица 7.4. Итерация 4
| (1,3) | (2,4) | (3,5) | −40 | (4,6) | −35 | (5,7) | −25 | (6,8) | −15 | s* | ||
| −10 | −15 | 285 Н | 225 Н | 125 Н | −10 Н | −10 | ||||||
| (2,1) | (3,2) | (4,3) | (5,4) | (6,5) | ||||||||
| 360 С | 280 Н | 175 Н | 80 С | |||||||||
| (3,1) | (4,2) | (5,3) | (6,4) | |||||||||
| 395 С | 285 С | 185 С | 90 С | |||||||||
| (4,1) | (5,2) | (6,3) | ||||||||||
| 300 С | 185 С | 95 С | ||||||||||
| (5,1) | (6,2) | |||||||||||
| 240 С | 115 С | |||||||||||
| (6,1) | ||||||||||||
| 130 С |
Итерация 5:
Таблица 7.5. Итерация 5
| (1,3) | (2,4) | −35 | (3,5) | −40 | (4,6) | −35 | (5,7) | −25 | (6,8) | −15 | s* | |
| −10 | 380 Н | 285 Н | 225 Н | 125 Н | −10 Н | −10 | ||||||
| (2,1) | (3,2) | (4,3) | (5,4) | (6,5) | ||||||||
| 465 С | 360 С | 280 Н | 175 Н | 80 С | ||||||||
| (3,1) | (4,2) | (5,3) | (6,4) | |||||||||
| 395 С | 285 С | 185 С | 90 С | |||||||||
| (4,1) | (5,2) | (6,3) | ||||||||||
| 300 С | 185 С | 95 С | ||||||||||
| (5,1) | (6,2) | |||||||||||
| 240 С | 115 С | |||||||||||
| (6,1) | ||||||||||||
| 130 С |
Итерация 6:
Таблица 7.6. Итерация 6
| (1,3) | −30 | (2,4) | −35 | (3,5) | −40 | (4,6) | −35 | (5,7) | −25 | (6,8) | −15 | s* |
| 455 Н | 380 Н | 285 Н | 225 Н | 125 Н | −10 Н | −10 | ||||||
| (2,1) | (3,2) | (4,3) | (5,4) | (6,5) | ||||||||
| 465 С | 360 С | 280 Н | 175 Н | 80 С | ||||||||
| (3,1) | (4,2) | (5,3) | (6,4) | |||||||||
| 395 С | 285 С | 185 С | 90 С | |||||||||
| (4,1) | (5,2) | (6,3) | ||||||||||
| 300 С | 185 С | 95 С | ||||||||||
| (5,1) | (6,2) | |||||||||||
| 240 С | 115 С | |||||||||||
| (6,1) | ||||||||||||
| 130 С |
Таким образом, оптимальная политика замен такова. Сразу, в начале 1-го года, меняем ис-ходную машину, проработавшую 3 года, на новую. Тем самым следующим является состояние (2,1). На этой машине работаем до начала 4-го года (состояние (4,3)), и опять меняем машину на новую, т.е. переходим в состояние (5,1). На последней машине работаем до конца срока, т.е. в течение 4-го, 5-го и 6-го годов. Переходы определяются буквами С и Н в левом нижнем столбце каждой ячейки. Максимальный доход составляет 455 единиц.
Заметим, что число состояний в данном случае равно 42, и использовать общую схему, т.е. заполнять вручную таблицы с 42-мя строками и ещё бóльшим числом столбцов, практичес-ки нереально. Здесь существенно использована специфика примера, приводящая к разделению множества состояний на слои. Как и в других примерах, связанных с заполнением таблиц, по-вторное заполнение похожих таблиц здесь делается только с демонстрационными целями. Ко-нечно, все данные можно последовательно записывать в одну и ту же таблицу, продвигаясь от правых столбцов к левым ■
Задание 1. Решить указанным в разделе 3.1.2 методом задачу о замене машины при следу-ющих данных о новых машинах:
Машина, новая в начале 1-го года
Машина, новая в начале 2-го года
Машина, новая в начале 3-го года
| Машина, новая в начале 4-го года
Машина, новая в начале 5-го года
Машина, новая в начале 6-го года
|
и различных данных об исходной машине:
Данные об исходной машине 1
| Возраст машины | ||||||
| Доход | ||||||
| Затраты на содержание | ||||||
| Затраты на замену |
Данные об исходной машине 2
| Возраст машины | ||||||
| Доход | ||||||
| Затраты на содержание | ||||||
| Затраты на замену |
Данные об исходной машине 1
