Свойства решений задач линейного программирования

Одним из основных понятий в теории ЛП является многогранник в 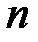- мерном пространстве и угловая точка. Перейдём к их определению.

Пусть 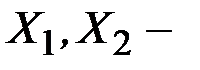две произвольные (различные) точки пространства .

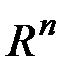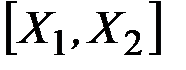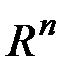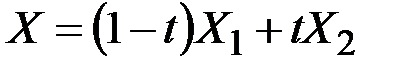Определение. Отрезком называется множество всех точек из вида , где 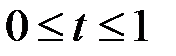. Точк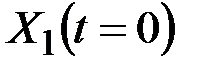и и 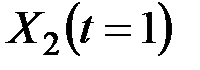называются концами отрезка, остальные точки называются внутренними.

Определение. Множество 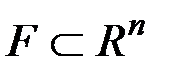называется выпуклым, если оно содержит вместе с каждыми двумя точками весь отрезок, содержащий эти точки.

Теорема 1.2. Пересечение выпуклых множеств есть выпуклое множество.

Доказать самостоятельно.

Определение. Гиперплоскостью в пространстве 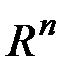называется совокупность точек 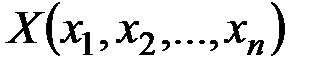, удовлетворяющих уравнению

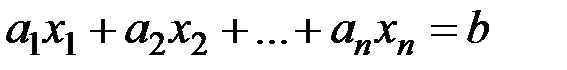, (1.10)

где хотя бы один из коэффициентов 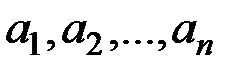отличен от нуля.

Определение. Полупространством в 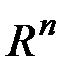называется множество точек

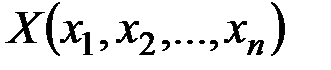, удовлетворяющих неравенству

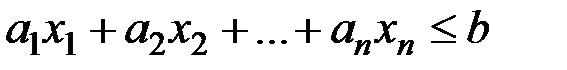(1.11)

или неравенству

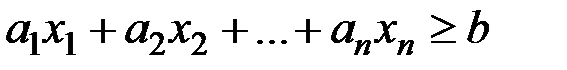. (1.12)

Ясно, что гиперплоскость (1.10) есть пересечение полупространств (1.11) и (1.12). Обозначая через А вектор 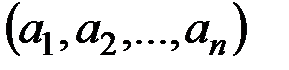, мы получим краткую запись гиперплоскости (1.10): AX=B и полупространств 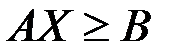, 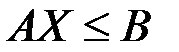. Теперь легко доказать следующую теорему:

Теорема 1.3. Всякое полупространство в 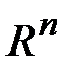является выпуклым множеством.

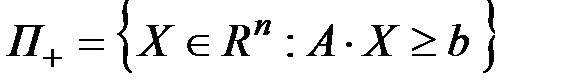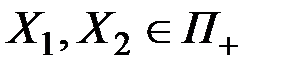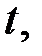
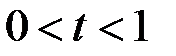
Доказательство. Рассмотрим . Пусть и пусть для произвольного 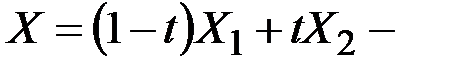любая точка отрезка .

.

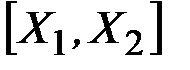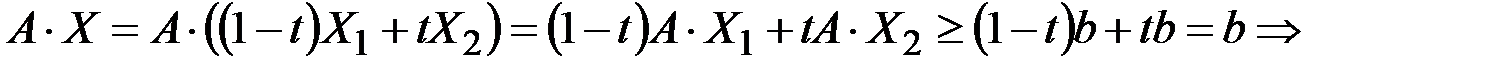
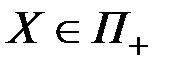Следствие. Всякая гиперплоскость в 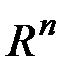является выпуклым множеством.

Определение. Пересечение конечного числа полупространств называется многогранной областью.

Определение. Ограниченная многогранная область называется многогранником.

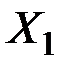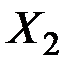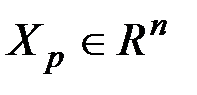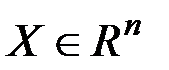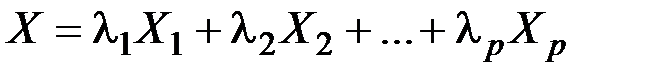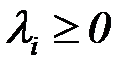Определение. Выпуклой линейной комбинацией векторов , , …, называется всякий вектор , допускающий представление , где и .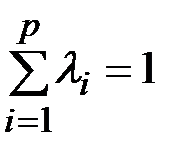

Определение. Точка множества 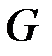называется угловой точкой, если она не является внутренней точкой отрезка, целиком принадлежащего .

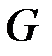Угловые точки многогранника называются его вершинами.

Теорема 1.4. Любая точка многогранника является выпуклой линейной комбинацией его угловых точек.

Теорема 1.5.(основная теорема ЛП). Целевая функция задачи ЛП достигает экстремума в угловой точке множества 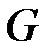допустимых решений , причём если целевая функция достигает экстремума в нескольких угловых точках множества допустимых решений, то она также достигает экстремума в любой выпуклой линейной комбинации этих точек.

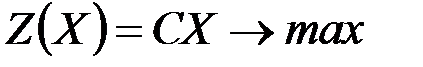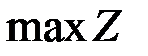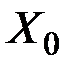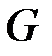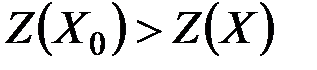
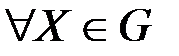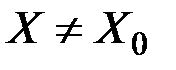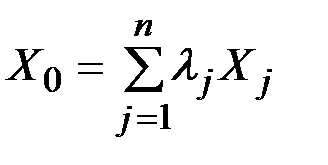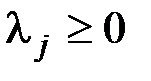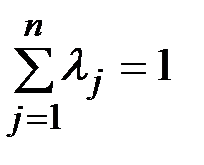Доказательство. Будем считать, что решается задача на максимум целевой функции, т.е. при системе ограничений (1.2). Доказательство проведём методом от противного. Предположим, что достигается во внутренней точке многогранника , т.е. , . Тогда по теореме1.4 , и , где 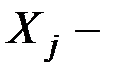угловые точки многогранника . Найдём

.

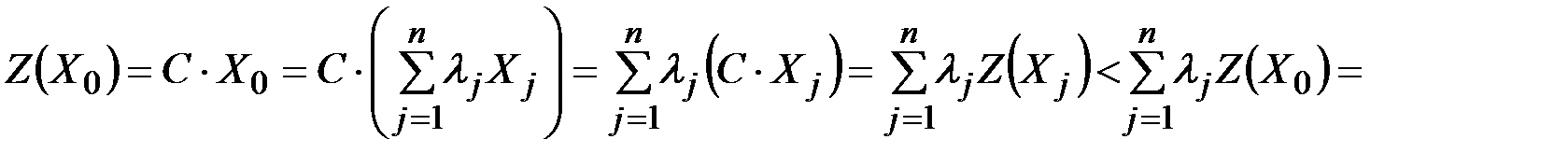
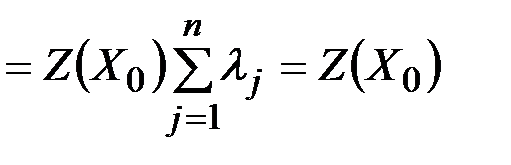
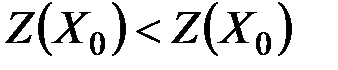Получено противоречие. Следовательно, 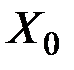является угловой точкой области допустимых решений.

Докажем второе утверждение теоремы. Пусть угловые точки 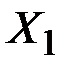, , 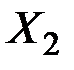…, 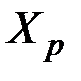являются оптимальными решениями, т.е.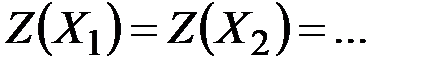 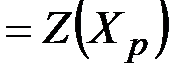и 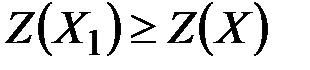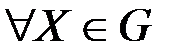. Найдём значение целевой функции для некоторой выпуклой линейной комбинации этих угловых точек: , , , .

,

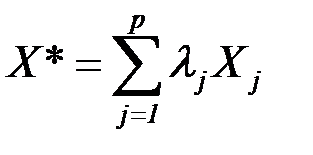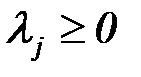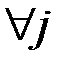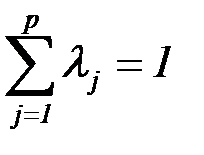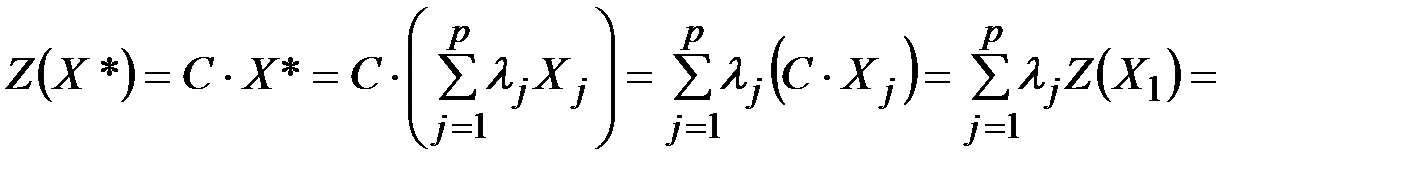
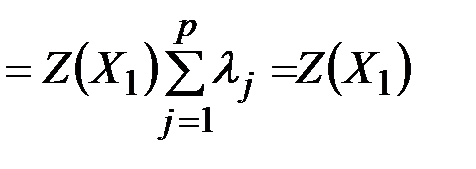т.е. решение 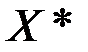также является оптимальным.

Рассмотрим каноническую задачу ЛП в векторной записи (см.(1.7)):

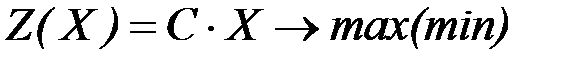
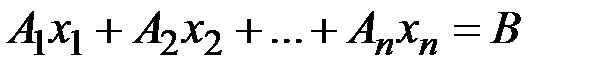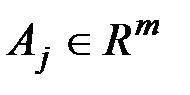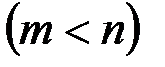, , (1.13)

.

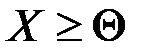Определение. Опорным решением задачи ЛП называется такое допустимое решение 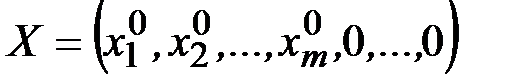, для которого соответствующие положительным координатам 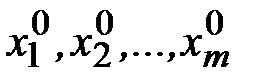векторы 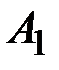, ,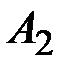…, 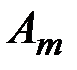в (1.13) линейно независимы.

Число отличных от нуля координат опорного решения не может быть больше ранга 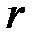системы векторов условия (т.е. числа линейно независимых уравнений системы ограничений). В дальнейшем будем считать, что система ограничений состоит из линейно независимых уравнений, т.е. 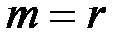. Если число отличных от нуля координат опорного решения равно 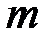, то оно (решение) называется невырожденным, в противном случае (меньше 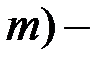вырожденным.

Определение. Базисом опорного решения называется базис системы векторов условия задачи (1.13), в состав которого входят векторы, соответствующие отличным от нуля координатам опорного решения.

Приведём без доказательства теоремы о взаимосвязи опорных решений и угловых точек множества допустимых решений.

Теорема 1.6.Любое опорное решение является угловой точкой области допустимых решений и наоборот, любая угловая точка области допустимых решений является опорным решением.