Правило обучения, корректирующее связи
Одно из главных преимуществ нейронных сетей заключается в том, что они предполагают наличие правил, с помощью которых сеть может программироваться автоматически. Например, можно рассмотреть еле-ующую функцию, реализующую вышеприведенное определение XOR.
Int XOR(int val_I, Int vai_2)
{
if (val_1= = 1&& val_2= =1)
return 0;
if(value_1= =0 && val_2= =0)
return 0;
if (val_1= = 1&& val_2= =0)
return 1;
if(val_1= =0 && val_2= =1)
return 1;
}
Нельзя сказать, что данный код оптимален и что данная функция не может быть реализована иначе. Мы уже видели, что сеть из примера 1.1 выполняет ту же задачу. Правильное выполнение операции XOR зависит от размещения элементов, выбора функции активности и набора весовых значений. Размещение элементов обычно фиксировано уже в начале обучения и точно так же оказывается заданной функция активности. Поэтому целью обучения является изменение весовых значений таким образом, чтобы в результате получить требуемые характеристики поведения сети.

Рис. 1.12. Взвешенная связь двух элементов. Сигнал х умножается на весовой коэффициент w. Для выходного элемента функция активности является тождественной функцией, что означает равенство вывода у взвешенному вводу
Типичной формой обучения является управляемое, обучение, когда для каждого набора данных, подающегося в процессе обучения на вход сети, соответствующий выходной набор известен. Обычно в начале обучения весовые коэффициенты устанавливаются равными случайным малым значениям, так что в первый раз при предъявлении сети учебного образца оказывается весьма маловероятным, чтобы сеть произвела верный вывод. Расхождение между тем, что даст сеть, и тем, что для данного учебного набора должно быть получено на самом деле, составляет ошибку, которая может использоваться для корректировки весов. Примером правила коррекции ошибок является дельта-правило, называемое также правилом Видроу—Хоффа (Widrow— Hoff rule). Взгляните на рис. (.12, где выходной элемент имеет активность (т.е. вывод) у, а истинный вывод должен быть равным /. Ошибка S задается следующей формулой:
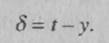
Сигнал, приходящий к выходному элементу, оюозначен через х. В соответствии с дельта-правилом, необходимо внести коррекцию
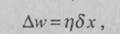 |
rw, вычисляемую по формулегде
Где h обозначает действительное число, называемое нормой обучения. Новый весовой коэффициент устанавливается равным сумме значений старого веса и коррекции:
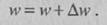 |
В алгоритме обучения выполнению операций типа XOR, который будет представлен в главе 2, используется обобщенная версия дельта-правила.
В начале обучения весовые коэффициенты устанавливаются равными малым случайным значениям; например, из диапазона [-0.3, +0.3]. В процессе обучения на вход сети подаются образец за образцом, и в результате их обработки весовые коэффициенты корректируются до тех пор, пока для всех вводимых образцов ошибки не станут меньше некоторого приемлемого достаточно малого значения. В завершение процесса сеть тестируется на данных, не представленных в фазе обучения: в результате можно оценить, насколько хорошо сеть работает с данными, которые в процессе обучения были ей неизвестны.
Обучение нейронной сети
Качество работы нейронной сети сильно зависит от предъявляемого ей в процессе обучения набора учебных данных. Учебные данные должны быть типичными для задачи, решению которой обучается сеть. Обучение часто оказывается уникальным процессом, когда приемлемые решения многих проблем могут быть получены только в процессе многочисленных экспериментов. Разработчикам решения на основе нейронной сети требуется следующее.
· Выбрать соответствующую модель сети
· Определить топологию сети (т.е. число элементов и их связи)
· Указать параметры обучения
Часто разработчику необходимо выполнить и предварительную подготовку данных. Такая предварительная подготовка может быть совсем простой, — например, перевод с помощью масштабирования значений всех признаков (т.е. переменных) в диапазон от 0 до 1, — а может включать использование и более сложных статистических процедур. Однако здесь следует подчеркнуть, что долгосрочной целью разработки нейронных сетей является минимизация необходимости прямого влияния разработчика на процесс нахождения решения, так как главным преимуществом Нейронных сетей является их потенциальная возможность вырабатывать собственные решения. На практике лучшие результаты получаются тогда, когда имеется четкое понимание рассматриваемой проблемной области знаний и концептуальное понимание проблем построения нейронной сети. Данные, используемые для обучения нейронной сети, обычно разделяются на две категории: одни данные используются для обучения, а другие — для тестирования. На самом деле реальные качества нейронной сети выявляются только во время тестирования, поскольку успешное завершение обучения сети должно означать отсутствие признаков неправильной работы сети во время ее тестирования. Процесс тестирования разрабатывается так, чтобы в его ходе для данной сети можно было бы оценить ее способность обобщать полученные знания. Обобщение в данном случае означает способность сети правильно выполнять задачу с данными, которые оказываются хотя и аналогичными данным, предъявлявшимся сети в процессе обучения, но все же отличными от них.
Простой пример обучения
Давайте рассмотрим относительно простую задачу и выясним, как для ее решения можно использовать самый простой тип нейронной сети. Наша сеть будет состоять только из одного входного и одного выходного элементов.
Многие из нас в школе на уроке физики выполняли эксперимент, в котором требовалось измерить отклонение металлической пластины в зависимости от приложенной к ней нагрузки — гирь определенного веса. Потом необходимо было начертить график отклонения в зависимости от веса приложенной нагрузки. График строился по точкам, которые должны были в идеале образовать прямую линию. Используя метод наименьших квадратов, по полученным точкам можно построить прямую линию, с помощью которой можно будет предсказать, насколько отклонится пластина под нагрузкой, для которой отклонение не измерялось. Многие проблемы моделируются с помощью построения прямых (или кривых) линий по имеющимся данным. Например, можно анализировать графики производства за прошедшие- несколько лет, чтобы оценить, сколько стиральных машин изготовит фирма в течение следующих двух лет. Если тенденция изменения данных соответствует прямой линии, мы получим нечто похожее на диаграмму, показанную на рис. 1.13, где данные располагаются вдоль прямой, хотя и не существует прямой линии, на которой они лежали бы в точности. Этого и следовало ожидать — в реальном мире при любом измерении всегда имеются ошибки.
Уравнение прямой задается формулой
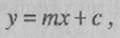
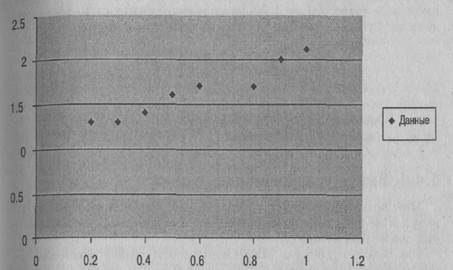 |
Рис, 1.13. Данные располагаются вдоль прямой линии, нб не лежат в точности на прямой из-за ошибок измерения
где у и х являются переменными (например, отклонением и нагрузкой), m определяет наклон или градиент прямой, а с — значение сдвига (т.е. точку, в которой прямая пересекает ось у). Можно провести прямую на глаз, а затем измерить ее наклон и значение сдвига, но метод наименьших квадратов дает нам возможность вычислить тис. Что означает "наиболее подходящая прямая"? В данном случае это прямая, для которой сумма квадратов ошибок для всех точек, соответствующих имеющимся данным, оказывается наименьшей. Что такое ошибки для набора точек, показано на рис. 1.14. Чтобы найти сумму квадратов ошибок, следует возвести значение каждой из ошибок в квадрат и просуммировать все полученные таким образом значения.
При использовании метода наименьших квадратов m находится по формуле
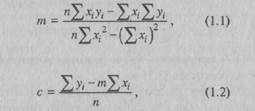 |
а с — по формуле
где хi и yi представляют значения координат для точки i, а п равно числу точек. Суммирование выполняется по всем точкам данных.

Рис. 1.14. Каждой точке соответствует своя ошибка, равная расстоянию от точки до прямой
Вывод уравнений для mис
Этот подраздел не является обязательным, но может оказаться полезным для лучшего понимания некоторых теоретических понятий, о которых пойдет речь в главе 2.
Как только с данными оказывается сопоставленной некоторая прямая, с помощью уравнения этой прямой для любого данного значения л можно получить оценку соответствующего значения у. В реальности любой оценке значения у соответствует своя ошибка. Поэтому для оценки v мы можем записать:
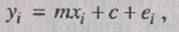 (1.3)
(1.3)
где ei обозначает ошибку для точки i. Сумма квадратов ошибок, Е, вычисляется по формуле
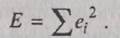 (1-4)
(1-4)
| Используя равенства (1.3) и (1.4), получаем: |
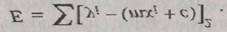 |
Теперь, рассмотрев частные производные уравнения (1.5), мы увидим. как зависит общая ошибка от изменения m и c:
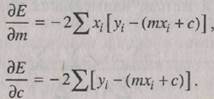 |
(1.6)
(1.7)
Если (1.6) и (1.7) приравнять к 0 и решить соответствующие уравнения, будут получены равенства (1.1) и (1.2).
Метод наименьших квадратов дает эффективный способ нахождения прямой, наилучшим образом соответствующей имеющемуся набору данных. Метод прост в применении, но его обоснование требует определенного уровня знания математики. Для нахождения прямой, соответствующей имеющемуся набору данных, можно использовать нейронную сеть. Такой сети нужно просто предоставить учебные данные и дать возможность обучиться на них.
Сеть с одним входным и одним выходным элементами была обучена проводить прямую линию на основе анализа имеющихся данных (см. рис. 1.13). В этой сети использовалась линейная функция активности. Задача требовала, чтобы сеть оценивала тис, поэтому тис являются параметрами сети (т.е. весовыми коэффициентами), значения для которых перед началом обучения были выбраны случайным образом из диапазона между -0.3 и +0.3. Модель сети показана на рис. 1.15. Данными для обучения были значения координаты х для каждой точки и соответствующие целевые значения координаты у. Вес с на входе имеет значение 1 (с, умноженное на 1, равно с; этот вес задает смещение). Для обучения сети использовалось дельта-правило, а норма обучения была выбрана равной 0.1. Обучение заканчивалось после рассмотрения каждой точки 10000 раз.
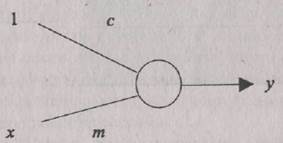
Рис. 1.15. Линейный элемент, который можно обучить найти прямую для данных на рис. 1.16
Оценки для тис, полученные с помощью сети, в результате применения метода наименьших квадратов, представлены в следующей таблице, а линия, найденная сетью, показана на рис.1.16.
| Параметр | Метод наименьших квадратов | Сеть |
| m | 1.0085 | 1.0284 |
| c | 1.0450 | 1.0360 |
На самом деле совсем не удивительно, что сеть по сравнению с методом наименьших квадратов дает сравнимые результаты, поскольку, как мы увидим в главе 2, дельта-правило обучения выводится из принципа минимизации суммы квадратов ошибок. Наша сеть решила данную задачу путем обобщения результатов вывода в зависимости от ввода, подобрав для них некоторую линейную зависимость. В нашем случае сеть моделирует прямую линию, но большие нейронные сети с нелинейными функциями активности могут подбирать для данных обучения весьма сложные формы и таким образом решать многие весьма сложные задачи.
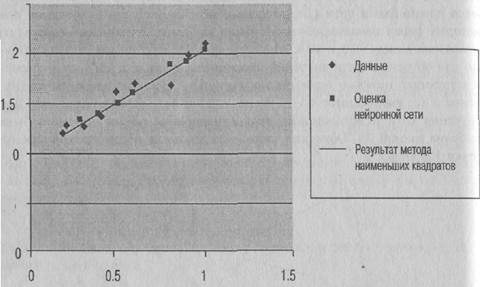 |
Рис. I 1б. Данные и соответствующая прямая, найденная с помощью нейронной сети, схема которой показана на рис. 1.15. Найденная нейронной сетью прямая мало отличается от прямой, получаемой при использовании метода наименьших квадратов
Резюме
• Нейронная сеть представляет собой совокупность простых обрабатывающих элементов, посылающих сигналы один другому по
взвешенным связям.
• Типы связей, допустимых между элементами в сети, зависят от
конкретной модели сети.
• Для каждого элемента сети имеется правило суммирования поступающих сигналов и правило вычисления выходного сигнала, посылаемого затем другим элементам сети. Правило вычисления выходного сигнала называется функцией активности. • Нейронная сеть может обучаться выполнению определенной задачи и обычно в привычном смысле не программируется. Обучение заключается в изменении значений весовых коэффициентов. В ходе обучения величина, на которую должен измениться весовой коэффициент, вычисляется с помощью соответствующего правила.
Андрей Масалович
Журнал доктора Добба
1992 - N 1 - с. 20-23
Идея создания нейрокомпьютеров, работа которых основана на использовании принципов функционирования мозга, возникла еще на заре компьютерной эры. В начале 40-х годов была разработана модель базового "процессорного элемента" мозга - нейрона, и были сформулированы основные принципы новой науки - нейроматематики. Однако уровень развития электроники в то время не позволял построить даже модель нервной системы муравья (примерно 20 тыс. нейронов), не говоря уже о мозге человека, этом сложнейшем продукте эволюции, содержащем более 100 млрд. нейронов.
Сегодня мы становимся свидетелями второго рождения нейроматематики. Прогресс микроэлектроники, с одной стороны, и кризис "нисходящего" подхода к построению систем искусственного интеллекта, с другой, обусловили новый взлет интереса к нейронным сетям и вычислительным системам на их основе. Современные нейрокомпьютеры способны распознавать речь и управлять самолетами, предсказывать изменения биржевых курсов и обнаруживать пусковые площадки ракет, а также решать множество других сложных задач. Из закрытых лабораторий университетов и военных фирм нейронные сети выходят в мир коммерческих систем, принося разработчикам миллионные прибыли.
Нейроматематика, нейронная сеть, нейрокомпьютер
Несмотря на впечатляющие успехи электронной индустрии остается довольно большое число задач, в решении которых самые быстродействующие компьютеры заметно уступают человеку и даже многим животным. Человек легко узнает лица и предметы, понимает речь, ориентируется в пространстве, анализирует динамические сцены.
Создание системы, способной не только эффективно решать перечисленные задачи, но и обладающей возможностями традиционных компьютеров, произвело бы настоящий переворот во многих прикладных областях. Особенно хорошо это понимают военные и промышленники, щедро субсидирующие перспективные разработки в данной области.
Работы по воспроизведению возможностей человеческого мозга традиционно ведутся по двум основным направлениям.
Сторонники так называемого "нисходящего" подхода, или символисты, концентрируют внимание на способах представления знаний и алгоритмах логического вывода. Это научное направление принято называть искусственным интеллектом (ИИ). Приверженцы "восходящего" подхода, или коннекционисты (от connection - соединение), изучают и стремятся воплотить в технических системах принципы организации естественных нейронных систем. К настоящему моменту в этой области знаний сложился некоторый набор моделей, называемых нейронными сетями. Наука, изучающая свойства таких сетей, называется нейроматематикой. Необходимо сразу подчеркнуть, что понятие "нейронная сеть" не подразумевает безусловного копирования биологических прототипов. Естественные нейронные системы рассматриваются как объект для подражания лишь в той мере, в которой это необходимо для эффективного решения тех или иных прикладных задач.
Наконец, нейрокомпьютер - это вычислительная система, реализующая какой-либо вариант нейронной сети. В последнее время появились также понятия нейроБИС, или нейрочип (реализация нейронной сети в виде интегральной микросхемы), и нейроплата (то же на печатной плате).
Теоретические основы нейроматематики были заложены в начале 40-х годов. В 1943 году У. Маккалох (U. Makkaloh) и его ученик У. Питтс (W. Pitts), которому в ту пору было 18 лет, сформулировали основные положения теории деятельности головного мозга. Ими были получены следующие результаты:
• разработана модель нейрона как простейшего процессорного элемента, выполняющего вычисление переходной функции от скалярного произведения вектора входных сигналов и вектора весовых коэффициентов;
• предложена конструкция сети таких элементов для выполнения логических и арифметических операций;
• сделано основополагающее предположение о том, что такая сеть способна обучаться, распознавать образы, обобщать полученную информацию.
Несмотря на то что за прошедшие годы нейроматематика ушла далеко вперед, многие утверждения Маккалоха остаются актуальными и поныне. В частности, при большом разнообразии моделей нейронов принцип их действия остается неизменным.
Подробнее о первых шагах нейроматематики можно прочесть в книге "Artificial Intelligence", (Amsterdam: Time-Life Books, 1986).
Модели нейрона
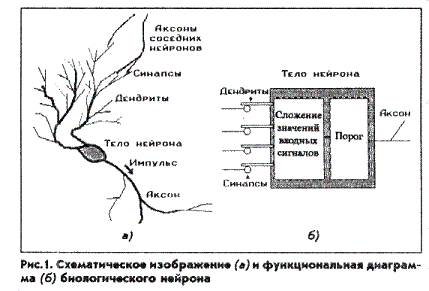
Нейронная сеть представляет собой совокупность большого числа сравнительно простых элементов - нейронов, топология соединений которых зависит от типа сети. Чтобы лучше понять структуру отдельного нейрона, обратимся к его прототипу - биологическому нейрону (рис.1, а). Биологический нейрон имеет тело, совокупность отростков - дендритов, по которым в нейрон поступают входные сигналы, и отросток - аксон, передающий выходной сигнал нейрона другим клеткам. Точка соединения дендрита и аксона называется синапсом.
В мозгу человека число "соседей" нейрона, соединенных с его дендритами, может достигать 10 тыс. Общее же число нейронов мозга превышает 100 млрд.
Упрощенно функционирование нейрона можно представить следующим образом (рис.1, 6):
1. Нейрон получает от дендритов набор (вектор) входных сигналов.
2. В теле нейрона оценивается суммарное значение входных сигналов. Однако входы нейрона неравнозначны (и это, пожалуй, самое важное наблюдение для понимания принципов действия нейронной сети). Каждый вход характеризуется некоторым весовым коэффициентом, определяющим важность поступающей по нему информации. Таким образом, нейрон не просто суммирует значения входных сигналов, а вычисляет скалярное произведение вектора входных сигналов и вектора весовых коэффициентов.
3. Нейрон формирует выходной сигнал, интенсивность которого зависит от значения вычисленного скалярного произведения. Если оно не превышает некоторого заданного порога, то выходной сигнал не формируется вовсе - нейрон "не срабатывает".
4. Выходной сигнал поступает на аксон и передается дендритам других нейронов.
Время срабатывания нейрона составляет примерно 1 мс, чуть меньше тратится на передачу сигнала между двумя нейронами. Таким образом, биологический нейрон - чрезвычайно медленно работающий процессорный элемент, уступающий по быстродействию современным компьютерам в миллионы раз. Тем более удивительно, что мозг в целом способен за доли секунды решать задачи, которые "не по зубам" даже суперкомпьютерам. Например, он может узнать лицо человека, показанное в непривычном ракурсе, и т.п.
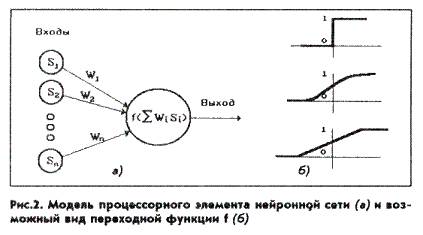
Модель нейрона - процессорного элемента нейронной сети, представлена на рис.2, а. В соответствии с вышеизложенным нейрон имеет набор входов, на которые поступают входные сигналы (Si,...,Sn). Входы характеризуются вектором весовых коэффициентов (W1,...,Wn). На рис.2,6 показаны некоторые возможные виды переходной функции f, вычисляемой от суммы взвешенных входных сигналов: пороговая, сигмовидная, псевдолинейная.
В зависимости от вида переходной функции нейроны делятся на два класса: детерминистские и вероятностные.
Различают два типа детерминистских нейронов:
1. Нейрон, в теле которого вычисляется скалярное произведение, (полностью соответствует рис.2, а). Это наиболее широко используемый тип нейрона. Он применяется в нейронных сетях для решения задач классификации и прогнозирования, а также для создания моделей ассоциативной памяти.
2. Нейрон "с ближайшим соседом", вычисляющий расстояние между входным вектором и вектором весовых коэффициентов и передающий полученное значение на выход. Такие нейроны применяют в нейронных сетях для решения задач квантования векторов, кластеризации, составления кодовых книг и т.д.
Вероятностный (стохастический) нейрон формирует выходное значение по следующему правилу:
у=1 с вероятностью Р(х)=1/(1+ехр(-ЬА))
у=0 с вероятностью 1 - Р(х).
Здесь х - вектор входных сигналов, А - скалярное произведение вектора входных сигналов и вектора весовых коэффициентов, у - выходной сигнал.
Вероятностные нейроны используют в моделях ассоциативной памяти и в нейронных сетях для решения задач классификации.
Подробнее о биологических нейронах можно прочесть в книге Дейхофф (J. Dayhoff) "Neural Network Architectures" (New York: Van Nostrand reinhold, 1990), а о моделях нейронов в нейронных сетях - в трудах конференции "Neural Computing" (London: IBC Technical Services, 1991).
Нейронные сети и алгоритмы их обучения.
Нейронная сеть (НС) - это совокупность нейронов, соединенных определенным образом. Она характеризуется типом используемых нейронов, их числом, топологией межсоединений (в том числе так называемой "слойностью" - числом уровней в иерархической структуре), а также принятым набором алгоритмов настройки (обучения).
Одной из наиболее простых НС является перцептрон, принципы построения которого предложены Ф. Розенблаттом (F. Rosenblatt) в 1958 году. Первоначально перцептрон представлял собой однослойную структуру с жесткой пороговой функцией процессорного элемента и бинарными или многозначными входами. Первые перцептроны были способны распознавать некоторые буквы латинского алфавита. Впоследствии модель перцептрона была значительно усовершенствована. На рис.3 представлен пример трехслойного перцептрона.
Помимо перцептрона существует несколько десятков разновидностей НС, наиболее известными из которых являются следующие:
• сеть Хопфилда - Коонена (Hopfield/Kohonen network) - модель ассоциативной памяти, представляющая собой однослойную сеть процессорных элементов с бинарными входами и жесткой пороговой функцией. Каждый процессорный элемент соединен со всеми соседями. Настройка весовых коэффициентов межсоединений производится по правилам Хеббиана (Hebbian rules);
• машина Больцмана (Boltzmann machine) -многослойная или случайным образом связанная НС. Настройка весовых коэффициентов производится на основе распределения Больцмана с использованием так называемого "температурного" параметра для определения кривизны вероятностной функции;
• НС с обратным прохождением (back propagation network), принцип действия которой базируется на вычислении отклонений значений сигналов на выходных процессорных элементах от эталонных и обратном "прогоне" этих отклонений до породивших их элементов с целью коррекции ошибки;
• неокогнитрон (neocognitron) - одна из наиболее сложных моделей НС. Это многослойная иерархическая сеть с двухсторонним прохождением сигналов, содержащая процессорные элементы двух видов: S-ячейки, выполняющие основную функцию сети, и С - ячейки, позволяющие корректировать позиционные ошибки во входных последовательностях. Неокогнитрон способен распознавать даже сильно зашумленные выборки.
Функционирование большинства НС (в частности, перцептрона) происходит в две стадии. На стадии настройки, или обучения, на вход НС подаются эталонные обучающие выборки и производятся вычисления в процессорных элементах промежуточных и выходного слоев сети. Затем проводят коррекцию и минимизацию ошибок путем перенастройки весовых коэффициентов (часто для этого данные "проводят" по сети в обратном направлении). На рис.4 в упрощенном виде приведен алгоритм обучения перцептрона. В житейских терминах, обучение НС сводится к следующему: "права" процессорных элементов, "нелояльных" к навязываемым сети решениям, впоследствии ограничиваются (знакомая картина, не так ли?). На стадии функционирования сети в рабочем режиме, соответствующем решению прикладных задач, дальнейшей настройки, как правило, не происходит. Однако возможны повторные сеансы обучения для улучшения характеристик сети либо для их адаптации к новым классам объектов.
Перечисленные выше типы НС нашли свое отражение в многочисленных реализациях нейроплат, нейроБИС и нейрокомпьютеров. Архитектура нейронных сетей подробно обсуждается в статье Р. Хёхт - Нилсена (R. Hecht - Nielsen) "Neuro - computing: picking the human brain" (IEEE SPECTRUM. -1988. - Vol.25, N 3. - P. 36-41).
