Раціональні і дійсні числа

Раціональні числа. Дії над ними та їх властивості

План

1. Поняття про вимірювання відрізків. Розширення множини цілих невід’ємних чисел.

2. Дроби та їх властивості.

3. Визначення арифметичних дій над додатними раціональними числами.

4. Закони додавання і множення.

5. Упорядкованість множини додатних раціональних чисел.

6. Запис додатних раціональних чисел у вигляді десяткових дробів.

Поняття про вимірювання відрізків. Розширення множини цілих невід’ємних чисел

Порівняння двох відрізків і дії над ними не завжди можна виконувати безпосередньо. Наприклад, один відрізок прямої з’єднує Москву і Київ, а другий Одесу і Мінськ. Як можна порівняти ці відрізки між собою? Як знайти їх суму, різницю?

Для цього потрібно виміряти ці відрізки, тобто знайти довжину кожного з них або відстань між їх кінцями.

Виміряти якусь величину — це означає порівняти її з іншою величиною такого ж роду, прийнятою за одиницю виміру.

Вимірювання величин, зокрема таких, як довжина, площа, об’єм, маса, час, виникло з практичних потреб людини в давні часи.

Для того, щоб уявити собі процес вимірювання, виберемо будь-який відрізок за одиничний, а за одиницю виміру довжини візьмемо довжину е цього відрізка. Тоді, щоб виміряти відрізок а, більший за одиничний, послідовно відкладатимемо одиничний відрізок на відрізку а (від його початку). Може бути два випадки:

1) одиничний відрізок вкладається в а всього n разів, де n — натуральне число. Тоді число n називають мірою відрізка а при оди­ниці виміру е і записують: а = nе.

2) одиничний відрізок е не вкладається ціле число разів у відріз­ку а, тобто не існує такого натурального числа n, щоб а = ne.

При цьому може трапитись, що, поділивши одиничний відрізок на п рівних частин, дістанемо нову одиницю виміру е₁ = 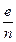, яка вкладається у відрізку а ціле число разів, наприклад т разів, тобто а=т ·е₁ = т ·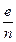

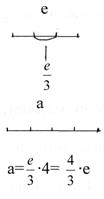
Цілком зрозуміло, що і при вимірюванні дрібнішими одиницями довжина не кожного відрізка виражатиметься натуральним числом. Звідси видно, що вимірювання довжин відрізків разом із діленням відрізка (або натурального числа, що є кількісною характеристикою певної скінченної множини) на рівні частини приводить до необхід­ності розширення множини цілих невід’ємних чисел введенням дро­бових чисел.

Дроби та їх властивості

Означення. Символ 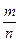, де т і п натуральні числа, називають дробом, т – чисельник дробу і п – знаменник.

Дріб 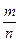означає, що одна п-на частина одиниці виміру е міститься т разів у відрізку а, тобто одиничний відрізок розділили на п рівних частин і взяти т таких частин. Це записується так: а = 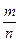е,

Дріб 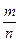є мірою довжини відрізка а при одиниці довжини е.

Повернемось до випадку 2) а = 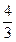е, це не єдиний розв’язок, бо якщо поділимо е на 6 рівних частин, то отримаємо а = 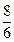е і т.д.

Тобто, довжина відрізка а може бути виражена нескінченною множиною дробів: , , , …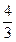

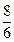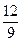Означення. Дроби, які виражають довжину одного і того ж відрізка при одиниці довжини е, називаються рівними.

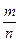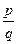Якщо дроби і рівні, то записують = .

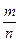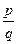Необхідна і достатня умова рівності дробів

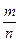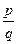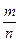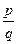
Два дроби і рівні тоді і тільки тоді, коли виконується умова mq=np, тобто = 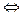mq=np

Доведення.

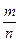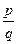
а) Доведемо, що = mq=np

Для будь-якого натурального числа q 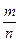= 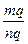, а для будь-якого натурального числа п = 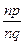. Тоді з рівності дробів 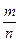і 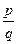випливає 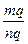= 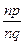. Оскільки знаменники цих дробів рівні, то і чисельники їх будуть рівні: mq=np.

б) Доведемо тепер, навпаки, що mq=np 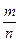= 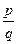. Розділимо обидві частини mq=np на натуральне число nq, тоді отримаємо 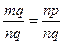. Але 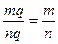, 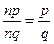. Тоді, = .

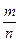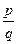Рівні дроби вважають різними записами одного і того ж числа, а саме число називають додатним раціональним числом.

Дріб – це лише форма зображення числа. Дробове число 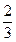можна зобразити (записати) різними рівними дробами: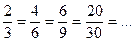

Дроби 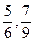, … зображають зовсім інші числа: 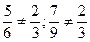і ін.

Для будь-якого додатного раціонального числа існує один і тільки один нескоротний дріб, що є записом цього числа.

Множина додатних раціональних чисел – це множина натуральних чисел в об’єднанні з множиною дробових чисел. Множину додатних раціональних чисел позначають Q₊. Множина натуральних чисел є підмножиною множини додатних чисел, тобто N 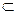Q₊.

Дріб, чисельник якого менший від знаменника, називається правильним; дріб, чисельник якого більший або дорівнює знаменнику, називається неправильним. Наприклад, 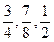– правильні; 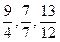– неправильні дроби.

Дріб 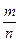, чисельник і знаменник якого є числа взаємно прості, тобто D(т;п)=1, називається нескоротним дробом.

Основна властивість дробу: Якщо чисельник і знаменник дробу помножити на те саме натуральне число, то дістанемо дріб, що дорівнює даному: , де k – натуральне число.

Застосування основної властивості дробу:

· скорочення дробів (заміна даного дробу іншим, що дорівнює йому, але з меншим чисельником і знаменником);

· зведення дробів до спільного знаменника (це заміна дробів рівними їм дробами, що мають однакові знаменники).

·

Наприклад.

1. Скоротити дріб .

1-ий спосіб: чисельник і знаменник дробу ділити послідовно на спільні прості дільники: 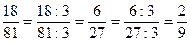, (2; 9) = 1

2-ий спосіб: знайти НСД чисельника і знаменника та поділити чисельник і знаменник відразу на їх НСД.

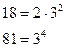
НСД (18; 81) = 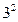= 9

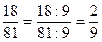, (2; 9) = 1.

2. Звести до найменшого спільного знаменника дроби:

а)

Знаменники цих дробів попарно взаємно прості. Тому НСК (3; 7; 10; 11) = =3 · 7 · 10 · 11 = 2310

Тоді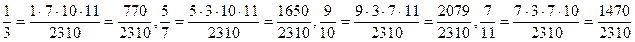

б)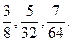

64:8 і 64:32, тому НСК (8; 32; 64) = 64.

Тоді

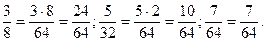
в)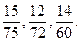

Маємо скоротні дроби, перед зведенням їх до найменшого спільного знаменника потрібно ці дроби скоротити.

Скоротимо ці дроби: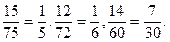

НСК (5; 6; 30) = 30

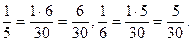
Отже,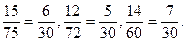

г) 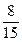і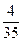

15 = 3 · 5, 35 = 5 · 7

НСК (15; 35) = 3 · 5 · 7 = 105.

Тоді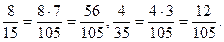

3. Побудувати відрізок, довжина якого виражена числом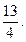

Побудова:

1) обираємо одиницю довжини е

2) ділимо відрізок е на 4 рівні частини

3) відкладаємо на промені Ох 13 відрізків, кожний з яких дорівнює четвертій частині відрізка е.

Отримаємо відрізок ОА, довжина якого виражена числом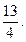

Поняття дробу вводять в початкових класах. За програмою з математики в 2 класі передбачено ознайомлення з частинами числа: половиною, третиною, чвертю, п’ятою частиною. В 3 класі учні розуміють сутність поняття частина числа; знаходять половину, третину, четверту на інші частини від числа, число за його частиною. В 4 класі розділ «Дроби». Тут за одиницю беруть відрізок, круг, прямокутник, зокрема квадрат, смужки та ін. Наприклад, круг ділять на 8 рівних частин і виділяють 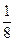частину круга, 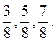Вводять поняття чисельника і знаменника дробу: число під рискою означає, на скільки рівних частин поділено ціле, його називають знаменником дробу. Число над рискою означає, скільки взято рівних частин. Це число називають чисельником дробу.

Учні записують і читають дроби; знаходять дріб від числа та число за його дробом; порівнюють дроби з однаковими знаменниками.