Горизонтально-слоистая модель
Определение поля плоской электромагнитной волны на поверхности горизонтально-слоистого полупространства является фундаментальной задачей магнитотеллурики. Такая модель называется одномерной. Ее описание приведено на рисунке 7.1. Модель состоит из N горизонтально однородных изотропных слоев, каждый из которых характеризуется определенными и постоянными значениями удельного сопротивления 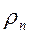
и мощности 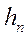 . Значения относительной диэлектрической и магнитной проницаемости слоев приняты равными единице. Мощность нижнего, N-го слоя равна бесконечности. Земная поверхность совпадает с плоскостью ХУ декартовой системы координат x,y,z. Ось z направлена сверху вниз. Верхнее полупространство (z<0) заполнено непроводящим воздухом.
. Значения относительной диэлектрической и магнитной проницаемости слоев приняты равными единице. Мощность нижнего, N-го слоя равна бесконечности. Земная поверхность совпадает с плоскостью ХУ декартовой системы координат x,y,z. Ось z направлена сверху вниз. Верхнее полупространство (z<0) заполнено непроводящим воздухом.
 Пусть по оси z сверху вниз распространяются две первичные, плоские монохроматические электромагнитные волны
Пусть по оси z сверху вниз распространяются две первичные, плоские монохроматические электромагнитные волны 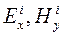 и
и 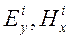 , эллиптически поляризованные в плоскости ХУ.
, эллиптически поляризованные в плоскости ХУ.
Процедура скаляризации позволяет представить полные вектора 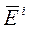 и
и 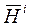 в виде суперпозиции скалярных составляющих по ортам.
в виде суперпозиции скалярных составляющих по ортам.
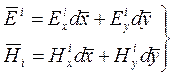 (7.1)
(7.1)
их скалярное произведение имеет вид:
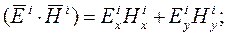
Вспомним, что из условия осевой симметрии среды и из определения импеданса плоской волны следует:
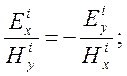
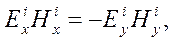
Следовательно, скалярное произведение 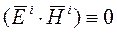 . Отсюда следует вывод, что комплексные вектора
. Отсюда следует вывод, что комплексные вектора  и
и 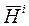 всегда ортогональны между собой. Из ортогональности векторов
всегда ортогональны между собой. Из ортогональности векторов 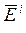 и
и 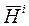 , а так же из (6.29) следует, что для определения импеданса на поверхности горизонтально-слоистой модели достаточно определить значение одной из сопряженных пар, например, составляющих Ех и Ну электромагнитного поля. Учитывая четвертый постулат модели Тихонова-Каньяра (уравнение 5.4), чтобы определить скалярную составляющую
, а так же из (6.29) следует, что для определения импеданса на поверхности горизонтально-слоистой модели достаточно определить значение одной из сопряженных пар, например, составляющих Ех и Ну электромагнитного поля. Учитывая четвертый постулат модели Тихонова-Каньяра (уравнение 5.4), чтобы определить скалярную составляющую 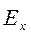 , достаточно решить одномерное уравнение Гельмгольца в декартовой системе координат.
, достаточно решить одномерное уравнение Гельмгольца в декартовой системе координат.
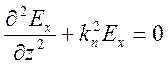 , (7.2)
, (7.2)
где 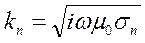 - волновое число n-го слоя.
- волновое число n-го слоя.
Общее решение уравнения (7.2) имеет вид
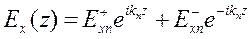 , (7.3)
, (7.3)
где 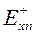 и
и 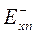 (n=1,2,…N) – некоторые, постоянные для каждого n-го слоя составляющие напряженности электрического поля по орту
(n=1,2,…N) – некоторые, постоянные для каждого n-го слоя составляющие напряженности электрического поля по орту 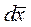 , зависящие от двух параметров – от удельного сопротивления n-го слоя и от частоты. Убывающая с ростом глубины z экспонента
, зависящие от двух параметров – от удельного сопротивления n-го слоя и от частоты. Убывающая с ростом глубины z экспонента 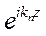 определяет совокупность плоско-однородных волн, распространяющихся сверху вниз, а возрастающая с ростом z экспонента
определяет совокупность плоско-однородных волн, распространяющихся сверху вниз, а возрастающая с ростом z экспонента 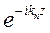 - совокупность отраженных волн, распространяющихся снизу вверх (см. уравнения 6.8 и 6.9).
- совокупность отраженных волн, распространяющихся снизу вверх (см. уравнения 6.8 и 6.9).
Для определения сопряженной компоненты магнитного поля Ну решим второе уравнение Максвелла 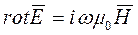 . Для скалярной компоненты Ну получим выражение
. Для скалярной компоненты Ну получим выражение
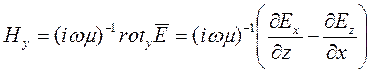 .
.
С учетом того, что в плоском поле отсутствуют вертикальные компоненты Ez и Hz и тождественно равны нулю все горизонтальные производные, следует
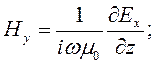 (7.4)
(7.4)
Подставляя (7.3) в (7.4), найдем
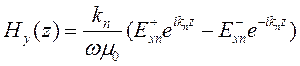 . (7.5)
. (7.5)
Таким образом, видно, что магнитное поле 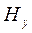 может быть выражено через те же константы
может быть выражено через те же константы 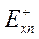 и
и 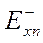 , что и электрическое поле
, что и электрическое поле 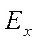 .
.
Теперь найдем, каким образом связан с параметрами среды магнитотеллурический входной импеданс 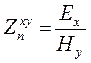 . Найдем из 7.3 и 7.5
. Найдем из 7.3 и 7.5
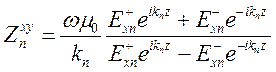 (7.6)
(7.6)
Поделим числитель и знаменатель (7.6) на 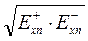
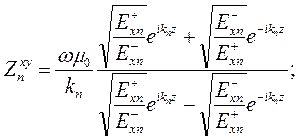 (7.7)
(7.7)
Введем обозначение 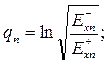
Тогда, 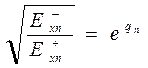 и
и 
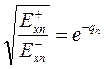 , отсюда
, отсюда
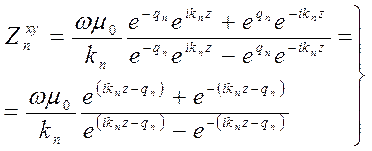
Обозначим 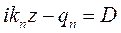 , тогда выражение для
, тогда выражение для 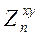 можно переписать в виде
можно переписать в виде
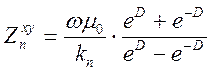
Далее, пользуясь понятием гиперболического котангенса, приведенным ниже в ссылке, найдем
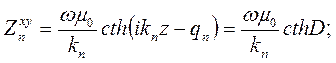 (7.8)
(7.8)
Из рисунка 7.1 можно видеть, что полученное выражение для импеданса 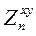 в n-м слое относится к интервалу глубин
в n-м слое относится к интервалу глубин
zn-1+0<z<zn-0
Две неизвестные постоянные 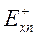 и
и 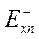 , входящие в (7.8) через выражение
, входящие в (7.8) через выражение 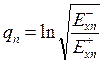 , могут быть определены, исходя из граничных условий о непрерывности горизонтальных составляющих поля
, могут быть определены, исходя из граничных условий о непрерывности горизонтальных составляющих поля 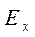 и
и 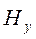 на границах слоев. Из них следует заключение о непрерывности их отношения, т.е. импеданса
на границах слоев. Из них следует заключение о непрерывности их отношения, т.е. импеданса 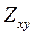 на границах слоев
на границах слоев
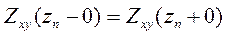 (7.9)
(7.9)
* Напомним гиперболические функции
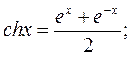
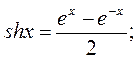
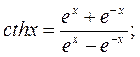
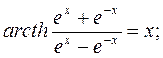
(7.9)
В левую часть (7.9) подставим значение 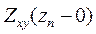 из 7.8
из 7.8
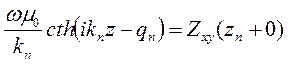
Теперь мы можем найти выражение для 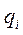 на верхней стороне i-й границы
на верхней стороне i-й границы 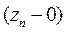 , используя пока неизвестные значения импеданса на нижней стороне n-й границы
, используя пока неизвестные значения импеданса на нижней стороне n-й границы 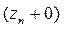
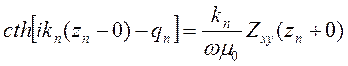 (7.10)
(7.10)
Поскольку 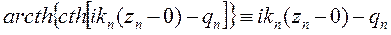 ,
,
то можно переписать (7.10) в следующем виде
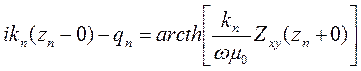 (7.11)
(7.11)
Теперь, пользуясь выражением для импеданса 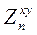 , действующего в слое n между его верхней границей
, действующего в слое n между его верхней границей 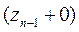 и нижней границей
и нижней границей 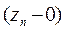 , можно найти выражение для рекуррентных соотношений, связывающих магнитотеллурические импедансы двух соседних слоев путем подстановки значений импеданса с кровли нижнего слоя
, можно найти выражение для рекуррентных соотношений, связывающих магнитотеллурические импедансы двух соседних слоев путем подстановки значений импеданса с кровли нижнего слоя 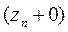 на подошву верхнего слоя
на подошву верхнего слоя 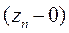 . Для этого в выражение (7.8) для импеданса
. Для этого в выражение (7.8) для импеданса 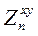 в слое n подставим значение
в слое n подставим значение 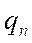 , выраженное в (7.11) через импеданс
, выраженное в (7.11) через импеданс 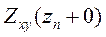 на кровле слоя n+1.
на кровле слоя n+1.
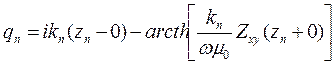 (7.11а)
(7.11а)
Если теперь подставить (7.11а) в (7.8), то мы получим выражение
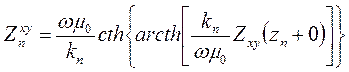 (7.11б)
(7.11б)
Однако, с учетом граничных условий при переходе с нижнего слоя на верхний, более правильной является следующая формула
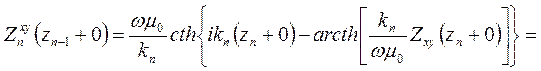
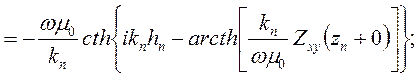 (7.12)
(7.12)
Полученное выражение (7.12) позволяет нам вычислить импеданс в каждом отдельно взятом n-м слое, пользуясь пока еще неизвестным значением импеданса в соседнем, залегающем ниже (n+1)-м слое. Перепишем их по слоям.
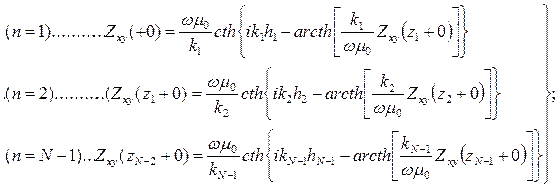 (7.13)
(7.13)
Теперь остается определить импеданс 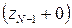 в подстилающем N-ом слое бесконечной мощности. Из самых общих соображений нетрудно оценить, что в нем нет отражений, и сохраняются лишь затухающие с ростом z экспоненты в решении уравнения Гельмгольца (7.3)
в подстилающем N-ом слое бесконечной мощности. Из самых общих соображений нетрудно оценить, что в нем нет отражений, и сохраняются лишь затухающие с ростом z экспоненты в решении уравнения Гельмгольца (7.3)
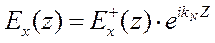 при
при 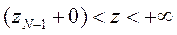 (7.14)
(7.14)
Раньше мы записали выражение (7.4) для сопряженной магнитной компоненты 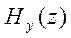 . Подставим в него
. Подставим в него 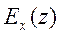 из (7.14)
из (7.14)
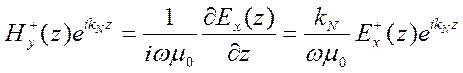 (7.15)
(7.15)
Можно видеть, что импеданс в основании слоистого разреза определяется явным образом
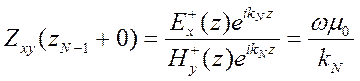 (7.16)
(7.16)
В него входят известные, заранее заданные в прямой задаче параметры 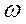 и
и 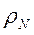 . Подставив (7.16) в (7.13), мы полностью определяем импеданс в вышележащем слое (N+1). Продолжая эту операцию в направлении снизу вверх (она называется рекурсией), мы доберемся до верхнего слоя
. Подставив (7.16) в (7.13), мы полностью определяем импеданс в вышележащем слое (N+1). Продолжая эту операцию в направлении снизу вверх (она называется рекурсией), мы доберемся до верхнего слоя 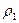 и определим импеданс
и определим импеданс 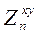 на поверхности n-слойного полупространства.
на поверхности n-слойного полупространства.
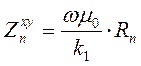 (7.16)
(7.16)
Где Rn- приведенный импеданс слоистого полупространства
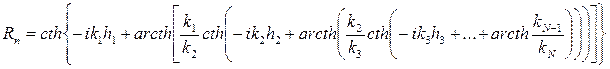 7.17)
7.17)
Для импеданса 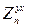 можно выполнить аналогичные вычисления, и они приведут к тому же результату [2.39, 2.40]. Таким образом, на поверхности слоистого полупространства можно заметить
можно выполнить аналогичные вычисления, и они приведут к тому же результату [2.39, 2.40]. Таким образом, на поверхности слоистого полупространства можно заметить
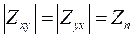
Его принято называть импедансом Тихонова-Каньяра, понимая под этим входной импеданс горизонтально-слоистого однородного разреза. Вычисляется он по отношению взаимно-ортогональных компонент электрического и магнитного полей, измеряемых на дневной поверхности Земли.
Величина приведенного импеданса 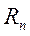 может быть определена как результат нормировки (деления) входного импеданса (аномального) на значение импеданса верхнего слоя
может быть определена как результат нормировки (деления) входного импеданса (аномального) на значение импеданса верхнего слоя 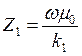 , принимаемого как «нормальный» импеданс однородного полупространства с удельным сопротивлением
, принимаемого как «нормальный» импеданс однородного полупространства с удельным сопротивлением 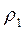 .
.
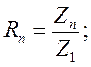 (7.18)
(7.18)
Отсюда можно записать, что рассчитываемое теоретически значение входного импеданса магнитотеллурического поля над горизонтально слоистой средой равно произведению импеданса Z1 для однородного полупространства, сопротивление которого равно сопротивлению первого слоя, на приведенный импеданс 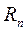 , отражающий влияние всех залегающих ниже слоев
, отражающий влияние всех залегающих ниже слоев
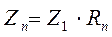 (7.18а)
(7.18а)
Кажущееся сопротивление по результатам описанного выше теоретического решения прямой задачи вычисляют по формуле
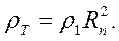 (7.18б)
(7.18б)
Обработка результатов МТЗ
Как уже отмечалось выше, основным информативным параметром МТЗ является импеданс. Импеданс плоской электромагнитной волны 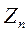 на поверхности слоистого n-слойного разреза определяется как входной импеданс. Он связан с параметрами этого разреза соотношением
на поверхности слоистого n-слойного разреза определяется как входной импеданс. Он связан с параметрами этого разреза соотношением
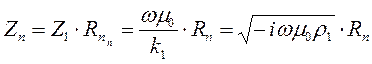 (8.1)
(8.1)
где 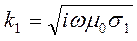 =
= 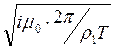 - волновое число верхнего слоя с сопротивлением
- волновое число верхнего слоя с сопротивлением 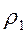 .
.
Rn - безразмерная величина, приведенный импеданс, определяемый с помощью рекуррентных соотношений (7.17). В частности, для двухслойного разреза выражение Rn имеет вид
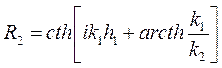 (8.2)
(8.2)
для трехслойного разреза
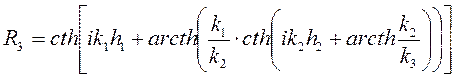 (8.3)
(8.3)
Если среда однородна 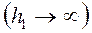 , то R1=1, т.к.
, то R1=1, т.к. 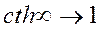 в (7.17). Следовательно
в (7.17). Следовательно
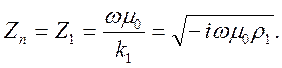 (8.4)
(8.4)
8.1. Амплитудные кривые МТЗ
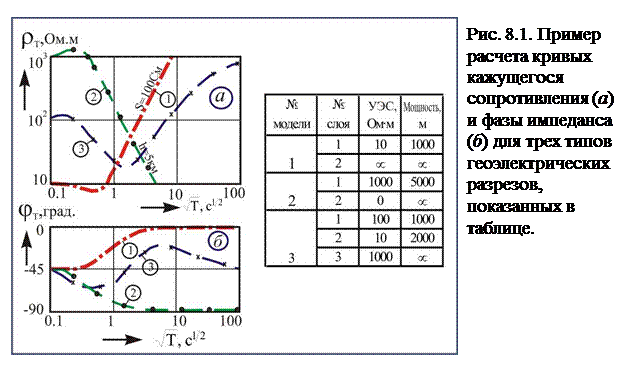
В основе теории количественной интерпретации МТЗ лежит построение кривых кажущегося электрического сопротивления 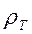 . Их называют амплитудными кривыми МТЗ и строят в двойном логарифмическом масштабе (рис. 8.1-а.). По оси ординат откладывают значения
. Их называют амплитудными кривыми МТЗ и строят в двойном логарифмическом масштабе (рис. 8.1-а.). По оси ординат откладывают значения 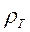 , а по оси абсцисс значения
, а по оси абсцисс значения 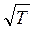 . Величина
. Величина 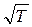 линейно пропорциональна глубине проникновения, определяемой толщиной скин-слоя
линейно пропорциональна глубине проникновения, определяемой толщиной скин-слоя 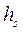 , где
, где 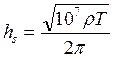 .
.
Кажущееся сопротивление, например, для сопряженных компонент Ех и Ну, согласно (4.8), определяют по формуле
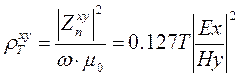 (8.5)
(8.5)
где 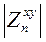 - модуль входного импеданса, определяемый по результатам обработки экспериментальных данных для сопряженных компонент Ех в мВ/км и Ну в мА/м. Входной импеданс при этом измеряется в единицах В/мА. Если среда однородна, то значение
- модуль входного импеданса, определяемый по результатам обработки экспериментальных данных для сопряженных компонент Ех в мВ/км и Ну в мА/м. Входной импеданс при этом измеряется в единицах В/мА. Если среда однородна, то значение 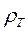 совпадает с ее удельным сопротивлением согласно (8.4). В общем случае одномерной горизонтально-слоистой среды значение
совпадает с ее удельным сопротивлением согласно (8.4). В общем случае одномерной горизонтально-слоистой среды значение 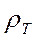 , рассчитанное теоретически, зависит от параметров разреза и от периода колебаний (частоты). Переходя к модулю и учитывая (7.18), можно записать
, рассчитанное теоретически, зависит от параметров разреза и от периода колебаний (частоты). Переходя к модулю и учитывая (7.18), можно записать
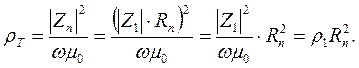 (8.6)
(8.6)
На высоких частотах, где 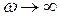 , но при этом поле остается в пределах квазистационарного приближения
, но при этом поле остается в пределах квазистационарного приближения 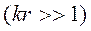 , можно записать
, можно записать 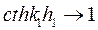 , следовательно
, следовательно
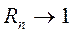 и
и 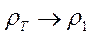 (8.7)
(8.7)
С понижением частоты на величину 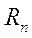 будут оказывать влияние все более глубокие слои. На самых низких частотах, где
будут оказывать влияние все более глубокие слои. На самых низких частотах, где 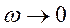 , но при этом поле остается в волновой зоне (r>>λ) при конечном сопротивлении основания
, но при этом поле остается в волновой зоне (r>>λ) при конечном сопротивлении основания 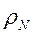 величина Rn, согласно (7.17), будет стремиться к значению
величина Rn, согласно (7.17), будет стремиться к значению 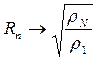 . Подставляя это значение Rn в формулу (8.6), получим
. Подставляя это значение Rn в формулу (8.6), получим
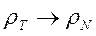 при
при 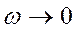 . (8.8)
. (8.8)
Таким образом, при изменении частоты происходит процесс частотного зондирования и на кривых кажущегося сопротивления (рис. 8.1-а) последовательно, с увеличением периода Т (с понижением частоты от условной бесконечности до условного нуля), последовательно проявляются все более глубоко залегающие слои. Если в основании разреза (рис. 8.1-а) залегает слой бесконечно высокого сопротивления 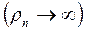 , то наблюдается восходящая кривая кажущегося сопротивления в виде асимптотической прямой, наклоненной к оси абсцисс под углом +63º25´ (кривая 1 на 8.1-а). Производная асимптоты
, то наблюдается восходящая кривая кажущегося сопротивления в виде асимптотической прямой, наклоненной к оси абсцисс под углом +63º25´ (кривая 1 на 8.1-а). Производная асимптоты 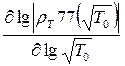 при этом стремится к значению 2. В случае хорошо проводящего основания
при этом стремится к значению 2. В случае хорошо проводящего основания 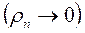 асимптотическая ветвь кривой кажущегося сопротивления имеет нисходящий вид и наклонена под углом -63º25´ к оси абсцисс (кривая 2 на рис. 8.1-а). Производная асимптоты
асимптотическая ветвь кривой кажущегося сопротивления имеет нисходящий вид и наклонена под углом -63º25´ к оси абсцисс (кривая 2 на рис. 8.1-а). Производная асимптоты 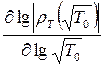 при этом стремится к значению -2.
при этом стремится к значению -2.
Приведенный импеданс Rn является комплексной величиной. Его фаза изменяется от 450 над разрезом с изолирующим основанием до -450 над разрезом с проводящим основанием и равна нулю над однородным полупространством.
Фазовые кривые МТЗ.
Фазовые кривые в методе МТЗ строят обычно для импеданса, представляющего собой отношение сопряженных компонент 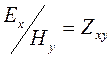 или
или 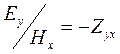 . Фаза импеданса, соответственно, определяется на логарифмической шкале как разность фаз сопряженных компонент.
. Фаза импеданса, соответственно, определяется на логарифмической шкале как разность фаз сопряженных компонент.
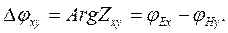
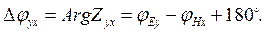 (8.9)
(8.9)
где 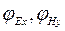 ,
, 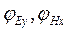 - значения фазы отдельных компонент в градусах.
- значения фазы отдельных компонент в градусах.
Входной импеданс над однородным полупространством имеет вид 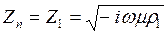 . Учитывая что
. Учитывая что 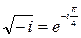 , фаза импеданса над однородным полупространством имеет значение
, фаза импеданса над однородным полупространством имеет значение
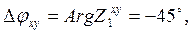 (8.10)
(8.10)
То есть график фазы импеданса над однородной средой имеет вид горизонтальной прямой на уровне -45º и не зависит от сопротивления среды и периода колебаний.
Над слоистым разрезом, в соответствии с (8.1) фаза импеданса определяется выражением
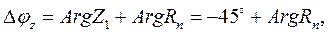 (8.11)
(8.11)
Поскольку 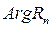 изменяется от +450 до -450 (раздел 8.1), то фаза импеданса над слоистым полупространством изменяется от 0 до -900
изменяется от +450 до -450 (раздел 8.1), то фаза импеданса над слоистым полупространством изменяется от 0 до -900
Подобно амплитудным, фазовые кривые отражают изменение удельного сопротивления и мощности слоев с глубиной, но только качественно, с точностью до некоторой неизвестной постоянной. Никакой новой информации об устройстве среды кривые фазы импеданса не приносят. Они могут быть получены из амплитудных кривых импеданса путем их дифференцирования, пользуясь дисперсионными соотношениями П. Вайдельта.
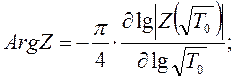 (8.12)
(8.12)
Фазовые кривые строят в линейно-логарифмическом масштабе: по оси ординат откладываются значения 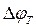 в градусах в линейном масштабе, по оси абсцисс, в логарифмическом масштабе – значения
в градусах в линейном масштабе, по оси абсцисс, в логарифмическом масштабе – значения 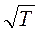 , где Т- период в секундах. Из рассмотрения (рис. 8.1) можно видеть, что породы высокого сопротивления приводят к уменьшению абсолютных значений разности фаз между компонентами импеданса, а породы низкого сопротивления – к обратной картине. На рис. 8.1 можно видеть, что при
, где Т- период в секундах. Из рассмотрения (рис. 8.1) можно видеть, что породы высокого сопротивления приводят к уменьшению абсолютных значений разности фаз между компонентами импеданса, а породы низкого сопротивления – к обратной картине. На рис. 8.1 можно видеть, что при 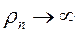 (разрез 1 в таблице) кривая фазы импеданса завершается горизонтальным участком
(разрез 1 в таблице) кривая фазы импеданса завершается горизонтальным участком 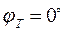 (кривая 1). Наоборот, при
(кривая 1). Наоборот, при 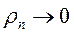 (разрез 2 в таблице) кривая фазы импеданса завершается горизонтальным участком
(разрез 2 в таблице) кривая фазы импеданса завершается горизонтальным участком 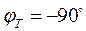 (кривая 2). Если же основание разреза имеет конечное сопротивление (разрез 3 на рис 8.1), то фаза импеданса, испытав минимум или максимум, возвращается к уровню -45˚, отмеченному выше для однородного полупространства.
(кривая 2). Если же основание разреза имеет конечное сопротивление (разрез 3 на рис 8.1), то фаза импеданса, испытав минимум или максимум, возвращается к уровню -45˚, отмеченному выше для однородного полупространства.
При интерпретации МТЗ фазовые кривые импеданса играют роль дополнительной информации, улучшающей качество и достоверность результатов решения обратной задачи. В процессе итерационного решения обратной задачи идет непрерывный поиск согласия между фазовыми и амплитудными кривыми.
Иногда, принято строить фазы кажущегося сопротивления. В этом случае соотношения Питера Вайдельта приобретают вид
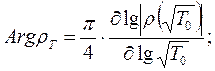 (8.13)
(8.13)
По внешнему виду формулы (8.12) и (8.13) отличаются только знаками. Но это не означает, что графики фазы импеданса и фазы сопротивления одинаковы по форме. Вид их существенно различен, так как разный вид имеют графики 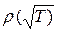 и
и 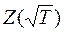 .
.
Поскольку мы уже знаем из раздела 8.1, что производная в выражении (8.13) изменяется от 2 для разреза ( 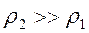 ) до -2 для разреза (
) до -2 для разреза ( 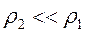 ), то соответствующие значения фазы кажущегося сопротивления над слоистым полупространством изменяются в пределах от +900 для восходящей кривой над разрезом с изолирующим основанием до -900 для нисходящей кривой над разрезом с бесконечно проводящим основанием. Общая картина поведения фазы кажущегося сопротивления сохраняет вид такой же, который был описан для фазы импеданса.
), то соответствующие значения фазы кажущегося сопротивления над слоистым полупространством изменяются в пределах от +900 для восходящей кривой над разрезом с изолирующим основанием до -900 для нисходящей кривой над разрезом с бесконечно проводящим основанием. Общая картина поведения фазы кажущегося сопротивления сохраняет вид такой же, который был описан для фазы импеданса.
Тензор импеданса.
Определение входного импеданса 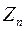 по наблюденным значениям компонент МТ-поля представляет собой наиболее сложную операцию при обработке полевых данных. Равенство
по наблюденным значениям компонент МТ-поля представляет собой наиболее сложную операцию при обработке полевых данных. Равенство 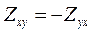 выполняется только лишь в условиях горизонтально-однородной слоистой среды, возбуждаемой однородным плоским линейно-поляризованным полем, т.е. в условиях модели Тихонова-Коньяра.
выполняется только лишь в условиях горизонтально-однородной слоистой среды, возбуждаемой однородным плоским линейно-поляризованным полем, т.е. в условиях модели Тихонова-Коньяра.
Реальная геологическая среда, как правило, горизонтально неоднородна. В этих условиях электрические и магнитные компоненты поля связаны между собой более сложными соотношениями. Эти соотношения вытекают из представления, что поле в земле возбуждается эллиптически поляризованной плоской электромагнитной волной, падающей сверху на дневную поверхность в виде двух линейно-поляризованных плоских волн, изменяющихся только по амплитуде 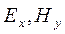 и
и 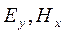 . В этом случае импеданс может быть представлен в виде тензора
. В этом случае импеданс может быть представлен в виде тензора
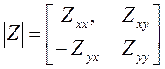 , (8.14)
, (8.14)
Где постоянные для данного разреза комплексные числа 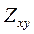 и
и 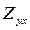 считаются главными, а
считаются главными, а 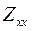 и
и 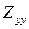 - дополнительными компонентами тензора импеданса. Пользуясь понятием тензора импеданса, можно представить горизонтальные компоненты электрического и магнитного полей в виде следующих соотношений
- дополнительными компонентами тензора импеданса. Пользуясь понятием тензора импеданса, можно представить горизонтальные компоненты электрического и магнитного полей в виде следующих соотношений
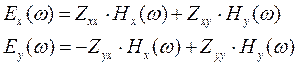 (8.15)
(8.15)
Регистрируя магнитотеллурические вариации при разных направлениях поляризации первичного поля, можно получить неограниченное число уравнений для определения четырех неизвестных (основных и дополнительных компонент тензора импеданса), характеризующих свойства подстилающего неоднородного полупространства. Иными словами, при изменении поляризации первичного поля изменяются фазы и амплитуды компонент поля Нх,Ну,Ех,Еу, измеряемые экспериментально и затем переводимые в частотную область,но неизменными остаются комплексные компоненты тензора импеданса 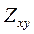 и
и 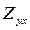 (основные) и
(основные) и 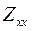 и
и 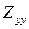 (дополнительные), представляющие основной интерес для суждения об электропроводности нижнего полупространства.
(дополнительные), представляющие основной интерес для суждения об электропроводности нижнего полупространства.
На следующем этапе, вращая систему координат ХУ, можно привести матрицу тензора импеданса к диагональному виду, отвечающему случаю, когда дополнительные компоненты тензора импеданса стремятся к нулю. Над одномерным горизонтально-слоистым разрезом диагональная матрица имеет вид
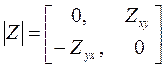 (8.16)
(8.16)
Такая схема называется системой главных осей тензора импеданса.
Тогда решение упрощается :
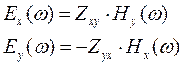 (8.17)
(8.17)
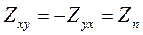 и
и 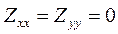
Существует большое множество программ обработки магнитотеллурических данных. Все они направлены на приведение матрицы тензора импеданса к диагональному виду (8.16). Если такая минимизация допустима в пределах погрешности, то среда считается одномерной и обратная задача решается в рамках одномерного приближения. Такая интерпретация называется формальной. Если матрица тензора импеданса не приводится к диагональному виду, то среда считается двумерной или трехмерной и интерпретация выполняется в рамках соответствующих моделей.
Двумерная модель МТЗ
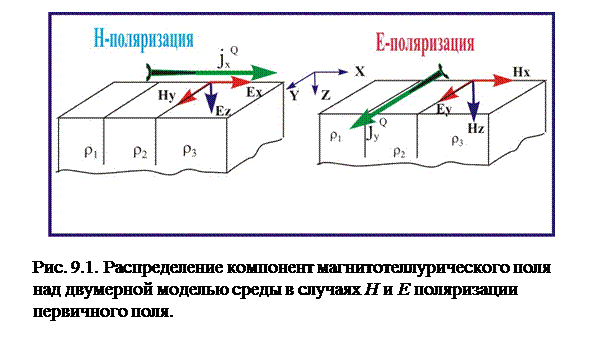
В случае двумерно неоднородной среды плоское эллиптически поляризованное поле может быть представлено в виде двух линейно поляризованных волн, ориентированных вдоль и вкрест простирания оси неоднородности структуры. Поле в этом случае распадается на две независимые системы уравнений, определяемые как E и H – поляризованные моды. Рассмотрим двумерную модель, в которой свойства среды не меняются вдоль оси У (рис. 9.1).
Выпишем первые два уравнения Максвелла с учетом плотности тока первичного источника JQ

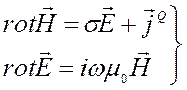
Распишем их, учитывая, что производные по координате У равны нулю, но появляются производные по координате Х наряду с производными по Z
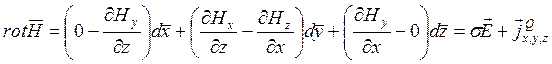 (9.1)
(9.1)
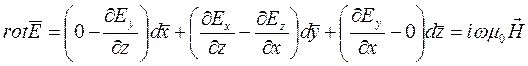 (9.2)
(9.2)
Здесь принято, что 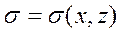 - произвольная функция двух координат в плоскости Х,Z.
- произвольная функция двух координат в плоскости Х,Z.
Из (9.1) и (9.2) выпишем скалярные составляющие по всем трем координатам
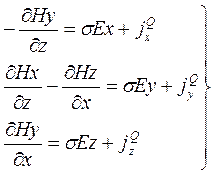
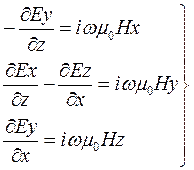 (9.3)
(9.3)
Отсюда могут быть составлены две группы не связанных между собой компонент поля для моделей Н-поляризации (поперечной) и Е-поляризации (продольной). Для начала рассмотрим случай Н-поляризации (Рис. 9.1), который соответствует случаю протекания первичного тока источника JQ вкрест простирания двумерной структуры. В этом случае вдоль простирания структуры поляризуется магнитное поле и по этой причине модель называется Н-поляризацией (поперечной). Очевидно, что в этом случае поле представлено тремя компонентами Ex, Ez, Hy. .
Н-поляризация 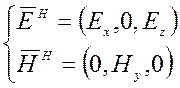
Из уравнений (9.3) находим
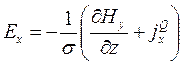
 (9.4)
(9.4)
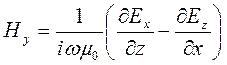 (9.5)
(9.5)
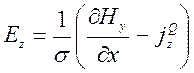 (9.6)
(9.6)
Подставив (9.4) и (9.6) в (9.5), находим для Н-поляризации (вне области первичного источника тока 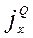 )
)
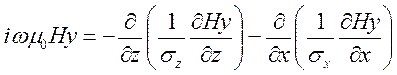 (9.7)
(9.7)
Электропроводность 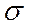 в (9.7) остается под знаком дифференцирования, поскольку в общем случае она меняется вдоль осей X и Z. Деля левую и правую части выражения (9.7) на
в (9.7) остается под знаком дифференцирования, поскольку в общем случае она меняется вдоль осей X и Z. Деля левую и правую части выражения (9.7) на 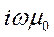 , получим двухмерное уравнение Гельмгольца:
, получим двухмерное уравнение Гельмгольца:
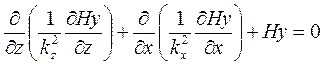 (9.8)
(9.8)
Заметим, что квадрат волнового числа остается под знаком дифференцирования, поскольку имеет разные значения в направлениях Х и У. 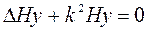
Определив из (9.8) компоненту 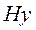 традиционным методом решения уравнения Гельмгольца по экспонентам, можно далее рассчитать
традиционным методом решения уравнения Гельмгольца по экспонентам, можно далее рассчитать 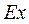 и
и 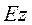 по формулам (9.4 и 9.6). Тем самым будет полностью решена задача для H-поляризации. Остается лишь рассчитать поперечный импеданс на земной поверхности
по формулам (9.4 и 9.6). Тем самым будет полностью решена задача для H-поляризации. Остается лишь рассчитать поперечный импеданс на земной поверхности 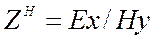 и построить амплитудные и фазовые кривые МТЗ для поперечной, H-поляризации.
и построить амплитудные и фазовые кривые МТЗ для поперечной, H-поляризации.
Аналогичным образом отыскивается уравнение Гельмгольца для Е-поляризации (продольной). Е-поляризация (рис.9.1) соответствует случаю протекания первичного тока источника JQ вдоль простирания двумерной структуры, по оси У. В этом случае вдоль простирания структуры поляризуется электрическое поле и модель называется Е-поляризационной (продольной). Очевидно, что в этом случае электромагнитное поле над двумерной структурой представлено тремя компонентами Нx, Нz, Еy. .
Е-поляризация 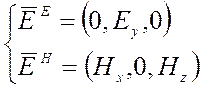
Из уравнений (9.3) находим
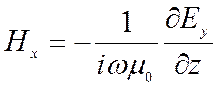 (9.9)
(9.9)
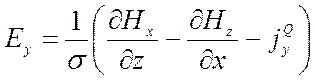 (9.10)
(9.10)
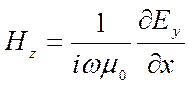 (9.11)
(9.11)
Подставив (9.9) и (9.11) в (9.10), получим (вне области первичного источника тока 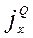 )
)
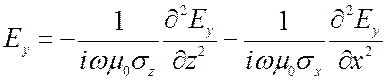
Отсюда следует уравнение Гельмгольца
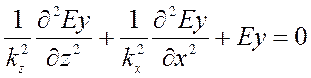
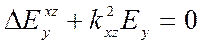 (9.12)
(9.12)
где 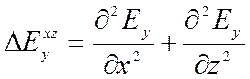 двумерный оператор Лапласа по
двумерный оператор Лапласа по 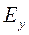
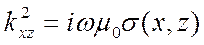 - волновое число по ортам Х и Z.
- волновое число по ортам Х и Z.
Электрическая компонента 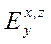 удовлетворяет двумерному уравнению Гельмгольца с переменным волновым числом k(x,z). После решения уравнения Гельмгольца (9.12) компоненты магнитного поля Hx и Hz , согласно (9.10) и (9.11), находятся путем простого дифференцирования по направлениям Х и Z компоненты поля
удовлетворяет двумерному уравнению Гельмгольца с переменным волновым числом k(x,z). После решения уравнения Гельмгольца (9.12) компоненты магнитного поля Hx и Hz , согласно (9.10) и (9.11), находятся путем простого дифференцирования по направлениям Х и Z компоненты поля 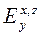 , найденной из (9.12) по экспонентам.
, найденной из (9.12) по экспонентам.
Таким образом, задача изучения двумерных полей сводится к отдельному решению двух задач, каждая из которых определяется с помощью двумерных уравнений Гельмгольца по одной скалярной функции Ну в случае Н-поляризации и по одной компоненте Еу в случае Е-поляризации.
Физическое истолкование поведения МТ поля над двумерной структурой может быть дано следующим образом. Н-поляризация наблюдается при поперечном протекании первичного тока, индуцированного магнитосферно-ионосферным источником  (рис. 9.1-а). Н-поляризации соответствуют кривые кажущегося сопротивления, измеренные с установкой MN , ориентированной поперек структур (Ех), и с магнитным датчиком (Ну), ориентированным вдоль структур. В этом случае они называются поперечными и обозначаются
(рис. 9.1-а). Н-поляризации соответствуют кривые кажущегося сопротивления, измеренные с установкой MN , ориентированной поперек структур (Ех), и с магнитным датчиком (Ну), ориентированным вдоль структур. В этом случае они называются поперечными и обозначаются 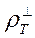 . Они наиболее сильно подвержены влиянию приповерхностных неоднородностей, или иначе влиянию так называемых гальванических эффектов. Это приводит к подъему кривых
. Они наиболее сильно подвержены влиянию приповерхностных неоднородностей, или иначе влиянию так называемых гальванических эффектов. Это приводит к подъему кривых 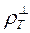 над приповерхностными плохо проводящими образованиями и к опусканию кривых над проводящими объектами. Гальванические эффекты при этом слабо проявляются на фазовых кривых. Постоянство фазовых кривых является главным признаком того, что изменения кривых кажущегося сопротивления обусловлены влиянием приповерхностных неоднородностей, или иначе влиянием так называемых статических (гальванических) искажений.
над приповерхностными плохо проводящими образованиями и к опусканию кривых над проводящими объектами. Гальванические эффекты при этом слабо проявляются на фазовых кривых. Постоянство фазовых кривых является главным признаком того, что изменения кривых кажущегося сопротивления обусловлены влиянием приповерхностных неоднородностей, или иначе влиянием так называемых статических (гальванических) искажений.
Е-поляризация соответствует продольному протеканию тока, индуцированного магнитосферно-ионосферным источником 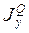 (рис. 9.1-б), относительно главных элементов линейной тектоники. Е-поляризация наблюдается при измерениях с установкой MN , ориентированной вдоль структур (Еу), и с магнитным датчиком (Нх), ориентированным поперек структур. В этом случае кривые кажущегося сопротивления называются продольными и обозначаются
(рис. 9.1-б), относительно главных элементов линейной тектоники. Е-поляризация наблюдается при измерениях с установкой MN , ориентированной вдоль структур (Еу), и с магнитным датчиком (Нх), ориентированным поперек структур. В этом случае кривые кажущегося сопротивления называются продольными и обозначаются 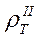 . Кривые
. Кривые 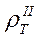 наиболее сильно искажены влиянием индукционных эффектов, вызванных преимущественной концентрацией теллурических токов в линейных проводящих структурах (рис. 9.1-б). Индукционные эффекты на кривых
наиболее сильно искажены влиянием индукционных эффектов, вызванных преимущественной концентрацией теллурических токов в линейных проводящих структурах (рис. 9.1-б). Индукционные эффекты на кривых 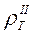 проявляются в изменении их формы, появлении ложных перегибов и минимумов, часто интерпретируемых как проводящие слои на глубине. В большинстве случаев такие слои являются фиктивными.
проявляются в изменении их формы, появлении ложных перегибов и минимумов, часто интерпретируемых как проводящие слои на глубине. В большинстве случаев такие слои являются фиктивными.
На рис. 9.2 приведен пример поперечной и продольной кривых кажущегося сопротивления для МТЗ, выполненного над серединой поднятия плохо проводящего кристаллического фундамента (горста, 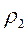 ), перекрытого сверху проводящим чехлом осадочных отложений (
), перекрытого сверху проводящим чехлом осадочных отложений ( 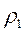 ) и подстилаемого снизу проводящим основанием (верхней мантией,
) и подстилаемого снизу проводящим основанием (верхней мантией, 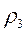 ). Эта модель соответствует в приближенном виде типу «К» (
). Эта модель соответствует в приближенном виде типу «К» ( 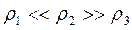 ).
).
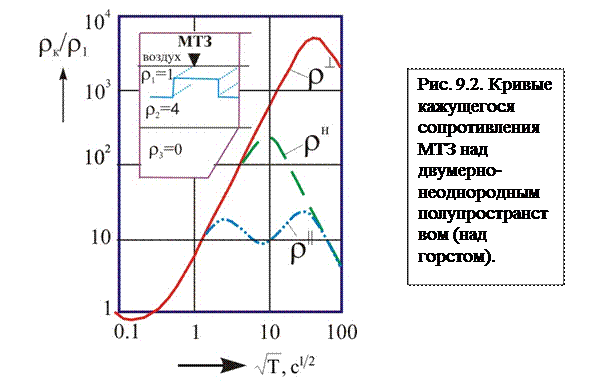
Видно, что поперечная кривая 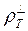 смещена вверх за счет концентрации поперечных токов над вершиной горста. Этот эффект сохраняется во всем диапазоне низких частот. Интерпретация кривой
смещена вверх за счет концентрации поперечных токов над вершиной горста. Этот эффект сохраняется во всем диапазоне низких частот. Интерпретация кривой 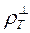 приводит к завышенной оценке как сопротивления фундамента, так и глубины залегания проводящего основания.
приводит к завышенной оценке как сопротивления фундамента, так и глубины залегания проводящего основания.
Продольная кривая 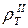 , наоборот, смещена вниз и, кроме того, искажена индукционным эффектом за счет продольной концентрации первичных токов, вдоль простирания горста. В диапазоне средних периодов (в районе Т=100 с) на ней наблюдается фиктивный промежуточный проводящий слой, которого на самом деле не существует. С понижением частоты этот эффект затухает. На самых длинных периодах (Т>1000 с) продольная кривая
, наоборот, смещена вниз и, кроме того, искажена индукционным эффектом за счет продольной концентрации первичных токов, вдоль простирания горста. В диапазоне средних периодов (в районе Т=100 с) на ней наблюдается фиктивный промежуточный проводящий слой, которого на самом деле не существует. С понижением частоты этот эффект затухает. На самых длинных периодах (Т>1000 с) продольная кривая 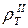 совпадает с «нормальной» кривой
совпадает с «нормальной» кривой 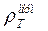 , рассчитанной для точки наблюдения над центром горста в предположении его бесконечной протяженности как по простиранию, так и по ширине. Эта часть кривой МТЗ дает правильную оценку глубины залегания проводящего основания (20 км). Поэтому при глубинных исследованиях методом МТЗ предпочтение отдают результатам интерпретации, выполненной на основании продольных кривых кажущегося сопротивления.В то же время, при изучении верхней части разреза, предпочтительной является поперечная поляризация. Полное решение обратной задачи с построением геоэлектрического разреза в условиях двумерно-неоднородных сред выполняется с применением итерационной процедуры на основе подбора обеих, Е и Н поляризаций.
, рассчитанной для точки наблюдения над центром горста в предположении его бесконечной протяженности как по простиранию, так и по ширине. Эта часть кривой МТЗ дает правильную оценку глубины залегания проводящего основания (20 км). Поэтому при глубинных исследованиях методом МТЗ предпочтение отдают результатам интерпретации, выполненной на основании продольных кривых кажущегося сопротивления.В то же время, при изучении верхней части разреза, предпочтительной является поперечная поляризация. Полное решение обратной задачи с построением геоэлектрического разреза в условиях двумерно-неоднородных сред выполняется с применением итерационной процедуры на основе подбора обеих, Е и Н поляризаций.
Интерпретация кривых МТЗ
Современные методы интерпретации результатов МТЗ полностью рассчитаны на применение компьютеров для решения обратной задачи в одномерном и двумерном приближениях. Однако, обратная задача некорректна и неоднозначна в принципе, т.к. незначительные изменения в исходных данных могут приводить к сильным изменениям в конечных результатах. Само решение обратной задачи ищется путем минимизации невязки между модельной и экспериментальной кривыми 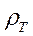 на основании многократных итерационных процедур. Невязка может быть весьма большой при неудачном выборе начального приближения. Поэтому для выбора стартовой модели, которая используется как параметр регуляризации, применяются методы экспресс-анализа, описываемые ниже.
на основании многократных итерационных процедур. Невязка может быть весьма большой при неудачном выборе начального приближения. Поэтому для выбора стартовой модели, которая используется как параметр регуляризации, применяются методы экспресс-анализа, описываемые ниже.
Асимптотический анализ.
Одним из наиболее простых и наглядных методов экспресс-анализа является метод определения обобщенных параметров разреза по асимптотическим формулам, вытекающим из решения прямой задачи МТЗ над горизонтально-слоистым разрезом, формулы (7.17) и (8.2). В качестве базовых применяются две альтернативные модели для двуслойных разрезов типа 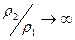 и
и 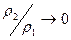 .
.
1. Модель I – разрез в виде пачки проводящих слоев, залегающих на непроводящем основании, 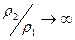 . Согласно низкочастотной асимптотике импеданса Тихонова-Каньяра в этом случае
. Согласно низкочастотной асимптотике импеданса Тихонова-Каньяра в этом случае
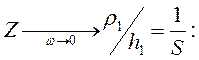
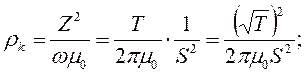 (10.1)
(10.1)
Прологарифмируем выражение (10.1)
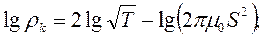 (10.2)
(10.2)
На билогарифмическом бланке 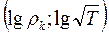 решение уравнения (10.2) принимает вид прямой линии, наклоненной под углом
решение уравнения (10.2) принимает вид прямой линии, наклоненной под углом 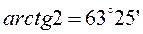 к оси абсцисс. В каждой точке этой прямой значение S определяется выражением
к оси абсцисс. В каждой точке этой прямой значение S определяется выражением
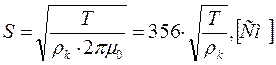 (10.3)
(10.3)
Если восходящей ветви 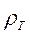 предшествует хорошо выраженный минимум, то продольная проводимость S надопорной толщи может быть определена по координатам минимума
предшествует хорошо выраженный минимум, то продольная проводимость S надопорной толщи может быть определена по координатам минимума
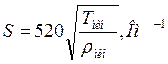 (10.4)
(10.4)
На фазовой кривой плохо проводящее основание проявляется выходом на значение 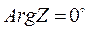 (рис. 8.1).
(рис. 8.1).
2. Модель II – разрез в виде плохо проводящей толщи, подстилаемой бесконечно хорошо проводящим основанием, 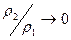 . Низкочастотная асимптотика Тихонова-Каньяра в этом случае имеет вид
. Низкочастотная асимптотика Тихонова-Каньяра в этом случае имеет вид
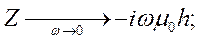
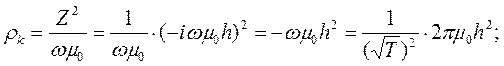 (10.5)
(10.5)
Прологарифмируем (10.5)
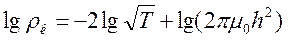 (10.6)
(10.6)
Уравнение (10.6) на билогарифмическом бланке 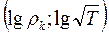 будет иметь вид прямой, наклоненной под углом -630.25΄ к оси абсцисс. При этом прямая будет являться геометрическим местом точек со значениями глубины h до проводящего основания, определяемыми выражением
будет иметь вид прямой, наклоненной под углом -630.25΄ к оси абсцисс. При этом прямая будет являться геометрическим местом точек со значениями глубины h до проводящего основания, определяемыми выражением
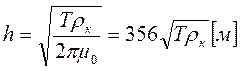 (10.7)
(10.7)
Фаза импеданса при этом выходит на прямую асимптотику со значением ArgZ=-900 (рис. 8.1).
Если нисходящей кривой предшествует максимум, то глубина до проводящего основания может быть определена с помощью приближённого выражения
 (10.8)
(10.8)
В качестве иллюстрации на рис.10.1-а приведена палетка асимптот МТЗ на фоне модели пятислойного разреза. Пользуясь попеременно асимптотиками S и h, можно оценить приближенно параметры геоэлектрического разреза.
Необходимо отметить, что в западной литературе широкое хождение получил способ изображения кривых МТЗ в координатах 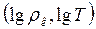 . В этом случае угол наклона асимптотики для описанных выше моделей I и II составляет arctg(±1)=±450. Все остальные описанные выше подходы к интерпретации кривых МТЗ по асимптотикам остаются в силе. Вид палетки асимптотик и кривых
. В этом случае угол наклона асимптотики для описанных выше моделей I и II составляет arctg(±1)=±450. Все остальные описанные выше подходы к интерпретации кривых МТЗ по асимптотикам остаются в силе. Вид палетки асимптотик и кривых 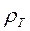 для этого способа изображения приведён на рис.10.1б в сопоставлении с принятым в отечественной литературе изображением тех же данных (рис.10.1а).
для этого способа изображения приведён на рис.10.1б в сопоставлении с принятым в отечественной литературе изображением тех же данных (рис.10.1а).
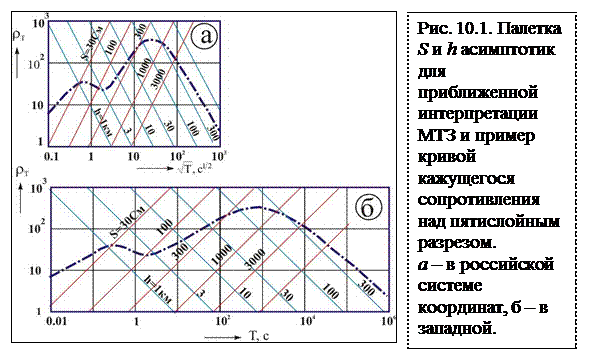
В заключение раздела приведем более подробный вывод низкочастотной асимптотики на примере двуслойного разреза с проводящим основанием [Крылов, 2004]. Формулу (8.2) для приведенного импеданса преобразуем, в более удобный вид, используя тригонометрическое правило 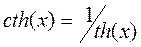 . В этом случае приведенный импеданс над двуслойным разрезом принимает вид.
. В этом случае приведенный импеданс над двуслойным разрезом принимает вид.
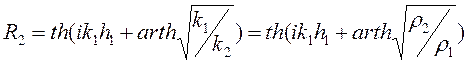 , (10.9)
, (10.9)
Поскольку при 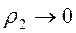
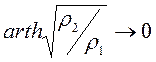 , то формула (10.9) принимает вид
, то формула (10.9) принимает вид
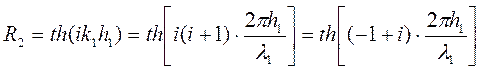 (10.10)
(10.10)
Переходя к модулю 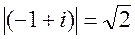 , и учитывая, что при длине волны, стремящейся к бесконечности в сравнении с мощностью верхнего слоя h1, величина
, и учитывая, что при длине волны, стремящейся к бесконечности в сравнении с мощностью верхнего слоя h1, величина 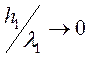 , можно принять, что гиперболический тангенс стремится к величине своего бесконечно малого аргумента. Отсюда можно записать.
, можно принять, что гиперболический тангенс стремится к величине своего бесконечно малого аргумента. Отсюда можно записать.
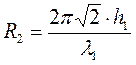 (10.11)
(10.11)
Поскольку модуль кажущегося сопротивления МТЗ над слоистым полупространством, согласно (8.6), определяется величиной 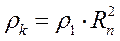 , то можно записать
, то можно записать
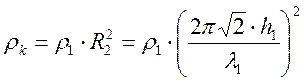 (10.12)
(10.12)
Подставив в (10.12) численное значение 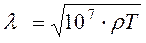 из (5.1), получим выражение для глубины до проводящего основания
из (5.1), получим выражение для глубины до проводящего основания
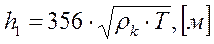 (10.13)
(10.13)
Мы получили выражение (10.13), совпадающее с ранее приведенным выражением (10.7). На билогарифмическом бланке 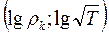 кривая
кривая 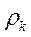 (чаще ее обозначают кривой
(чаще ее обозначают кривой 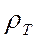 ) над разрезом с бесконечно проводящим основанием, имеет вид нисходящей прямой, наклоненной под отрицательным углом (-630.25΄) к оси абсцисс. Она называется Н-асимптотой, или иначе геометрическим местом точек со значениями глубины h до проводящего основания, определяемыми выражением (10.13).
) над разрезом с бесконечно проводящим основанием, имеет вид нисходящей прямой, наклоненной под отрицательным углом (-630.25΄) к оси абсцисс. Она называется Н-асимптотой, или иначе геометрическим местом точек со значениями глубины h до проводящего основания, определяемыми выражением (10.13).
