Основные дифференциальные соотношения теории изгиба

Пусть брус нагружен произвольным образом распределенной нагрузкой (рис. 6.12,а).

Рис. 6.12

Выделим из бруса элемент длиной 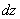и приложим по его краям положительные внутренние усилия (рис. 6.12,б). В пределах малого отрезка 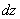нагрузку можно считать распределенной равномерно. Приравняем нулю сумму проекций всех сил на вертикальную ось y и сумму моментов всех сил относительно поперечной оси x, прохо­дящей через точку С (рис. 6.12,б), получим:

;

.

Производя упрощения и отбрасывая величины высшего поряд­ка малости, получим теорему Журавского (теорему Шведлера):

откуда

Указанные дифференциальные зависимости при изгибе позволяют установить некоторые особенности эпюр поперечных сил и изгибающих моментов.

1. Эпюра Q является прямолинейной на всех участках. На тех участках, где нет распределенной нагрузки, эпюра Q ограничена прямыми, параллельными оси эпюры, а эпюра М, в общем случае, – наклонными прямыми (рис. 6.13).

2. На тех участках, где к балке приложена равномерно распределенная нагрузка, эпюра Q ограничена наклонными прямыми, а эпюра М – квадратичными параболами (рис. 6.14). При построении эпюры М на сжатых волокнах, выпуклость параболы обращена в сторону, противоположную действию распределенной нагрузки (рис. 6.15,а, б).

Рис.6.13

Рис.6.14

3. В тех сечениях, где Q = 0, касательная к эпюре М параллельна оси эпюры (рис. 6.14, 6.15). Изгибающий момент в таких сечениях балки экстремален по величине (М_max, M_min).

4. На участках, где Q>0, M возрастает, то есть слева на право положительные ординаты эпюры M монотонно увеличиваются, отрицательные – монотонно уменьшаются (рис. 6.13, 6.14); на тех участках, где Q < 0, M убывает (рис. 6.13, 6.14).

5. В тех сечениях, где к балке приложены сосредоточенные силы:

а) на эпюре Q будут скачки на величину и в направлении приложенных сил (рис. 6.13, 6.14).

б) на эпюре M будут переломы (рис. 6.13, 6.14), острие перелома направлено против действия силы.

6. В тех, сечениях, где к балке приложены сосредоточенные моменты, на эпюре M будут скачки на величину этих моментов, на эпюре Q никаких изменений не будет (рис. 6.16).

Рис.6.15

Рис.6.16

7. Если на конце консоли или в концевой опоре приложен сосредоточенный момент, то в этом сечении изгибающий момент равен внешнему моменту (сечения C и B на рис. 6.16).

8. Эпюра Q представляет собой диаграмму производной от эпюры M. Значит, ординаты Q пропорциональны тангенсу угла наклона касательной к эпюре M (рис. 6.14).

9. Порядок линии на эпюре Q всегда на единицу меньше, чем на эпюре M. Например, если эпюра M - квадратная парабола, то эпюра Q на этом участке - наклонная прямая; если эпюра M - наклонная прямая, то эпюра Q на этом участке - прямая, параллельная оси; если M =const (прямая, параллельная оси), то на этом участке Q=0.