Специальный класс задач динамического программирования
Пусть требуется минимизировать функцию
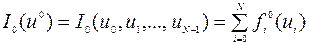(9.4.1)
при условиях:
, 
, 
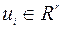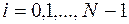, (9.4.2)
, 
, 
, 
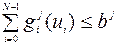, (9.4.3)
где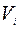 
– заданные множества из 
, 
, 
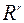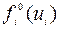, – заданные функции, 
– заданные числа.
Задачу (9.4.1)–(9.4.3) можно записать в виде задачи (9.1.5)–
(9.1.8). Введем переменные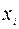 
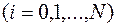как решение системы
, 
, 
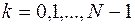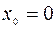, (9.4.4)
где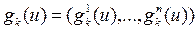 
, 
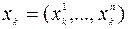
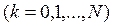. Так как из (9.4.4) следует что 
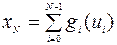, то ограничения (9.4.2) равносильны условию
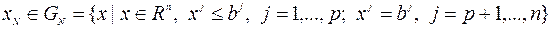.(9.4.5)
Таким образом, задача минимизации (9.4.1)–(9.4.3) эквивалентна задаче минимизации функции (9.4.1) при условиях (9.4.2), (9.4.4), (9.4.5) и является частным случаем задачи (9.1.5)–(9.1.8) при
, 
, 
, 
,
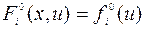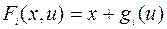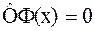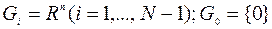а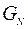 
определено соотношением (9.4.5). Следовательно, для решения задачи (9.4.1)–(9.4.3) может быть применен метод динамического программирования.
Используя введенные обозначения, перепишем уравнения Беллмана (9.2.5), (9.2.6)
Bk (x)= 
, , 
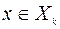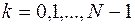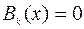. (9.4.6)
Уравнениями (9.4.6) можно пользоваться для решения задачи (9.4.1)–(9.4.3) методом Беллмана.
Вопросы и задания для самопроверки
Основные вопросы
1. Примеры постановок задач оптимизации.
2. Формулировка задачи оптимизации. Задачи теории оптимизации.
3. Понятие локального, глобального экстремума.
4. Проблема существования решения (Теорема Вейерштрасса, ее следствие)
5. Градиент функции. Линейное локальное представление функции.
6. Гессиан. Локальное квадратичное представление функции.
7. Классы функций (Выпуклые, сильновыпуклые). Свойства выпуклых функций.
8. Условия экстремума в задаче безусловной оптимизации.
9. Существование и единственность решения в задаче безусловной минимизации.
10. Скорости сходимости последовательностей.
11. Методы спуска. Релаксационные процессы.
12. Условия выбора направления спуска.
13. Условия выбора шага спуска.
14. Теорема о скорости сходимости методов спуска.
15. Градиентный метод. Оценка скорости сходимости.
16. Метод Ньютона. Оценка скорости сходимости.
17. Сопряженные направления. Метод сопряженных градиентов.
18. Принципы организации методов одномерного спуска.
19. Формы задач ЛП.
20. Графическое решение задачи ЛП.
21. Базисные допустимые решения (БДР) задачи ЛП.
22. Переход от одного БДР к другому в симплекс-методе (СМ).
23. Критерий выбора выгодного столбца в СМ (обоснование).
24. Симплекс – метод решения задачи ЛП.
25. Двухэтапный симплекс-метод.
26. Двойственная задача ЛП.
27. Транспортная задача. Нахождение БДР.
28. Метод потенциалов решения транспортной задачи.
29. Постановки задач целочисленного программирования (ЗЦП).
30. Точные методы решения ЗЦП.
31. Локальные методы решения ЗЦП.
32. Условия экстремума в задаче условной минимизации на простых множествах.
33. Метод проекции градиента.
34. Метод условного градиента.
35. Условия экстремума в задачах с ограничениями равенствами.
36. Метод линеаризации.
37. Метод Эрроу-Гурвица.
38. Метод штрафных функций.
39. Необходимые условия экстремума общей задачи нелинейного программирования (НЛП).
40. Достаточные условия экстремума общей задачи НЛП.
41. Необходимые и достаточные условия экстремума в задаче выпуклого программирования.
42. Постановка задачи оптимального управления. Функция и уравнение Беллмана
43. Метод динамического программирования
44. Специальный класс задач динамического программирования
45. Классические задачи вариационного исчисления (ВИ).
46. Необходимые условия оптимальности в задачах ВИ.
47. Достаточные условия оптимальности в задачах ВИ.