Метод последовательной верхней релаксации

Лекция 6. Метод релаксации

Большинство итерационных методов решения СЛАУ:

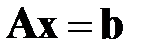(6.1)

Основаны на идее расщепления матрицы системы. Если представить матрицу 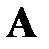в виде:

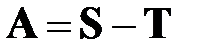, (6.2)

систему (6.1) можно переписать в виде:

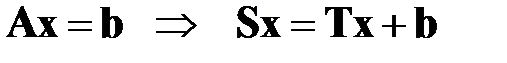(6.3)

и, на основании (6.3) использовать для итераций следующую формулу:

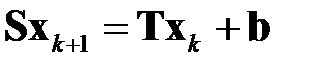(6.4)

Здесь сразу возникает два вопроса:

1. Не будет ли решение системы (6.4) слишком сложной задачей?

2. Будет ли последовательность сходиться к точному решению системы (6.1)?

Ответ на первый вопрос достаточно прост. Все зависит от того как расщепить матрицу 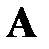(см(6.2)). Очевидно, что определение 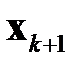из (6.4) будет несложным, если матрица 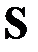будет диагональной, или, хотя бы треугольной.

Например, если матрицу

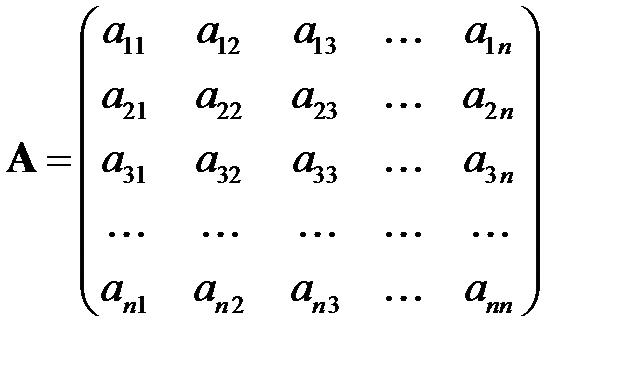(6.5)

расщепить следующим образом:

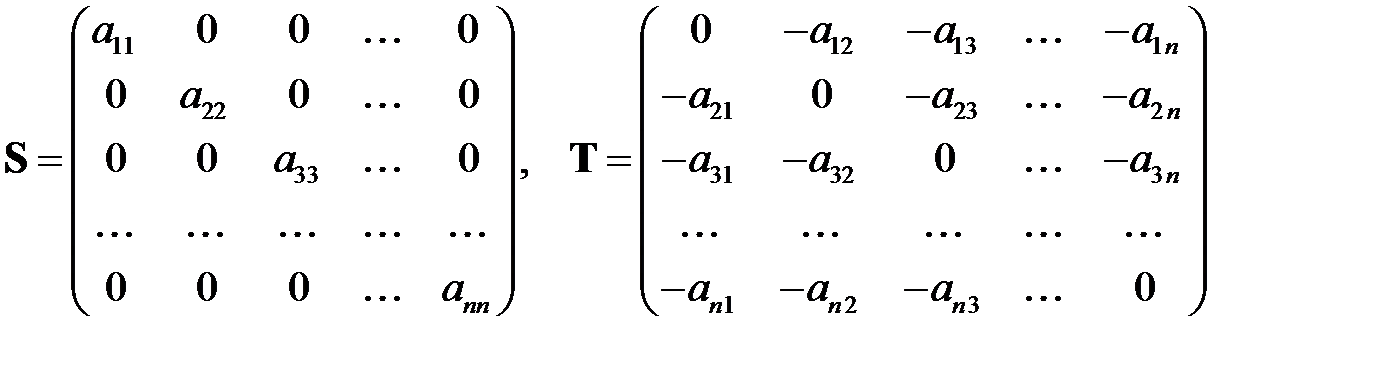(6.6)

то формула (6.4) определит уже известный нам метод Якоби.

Если же выбрать 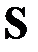нижней треугольной, а 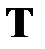‑ верхней строго треугольной:

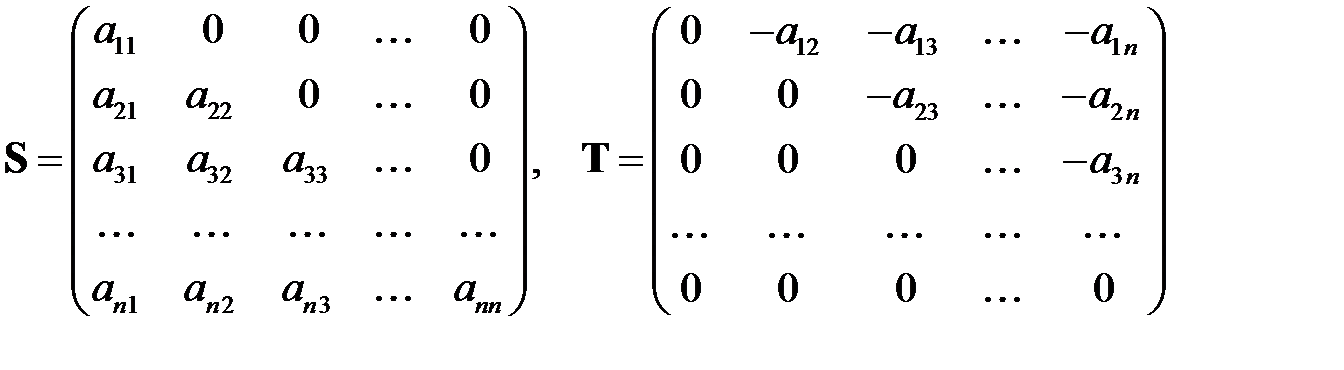(6.7)

формула (6.4) будет определять метод Гаусса-Зейделя.

Для того, чтобы прояснить ответ на второй вопрос, вычтем из уравнения (6.3) уравнение (6.4):

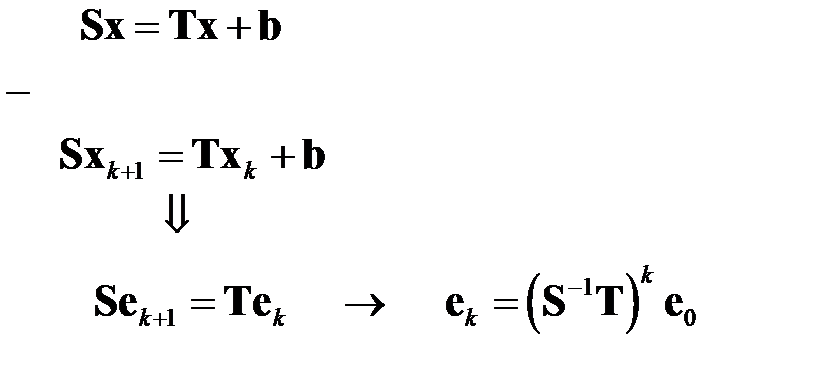(6.8)

Здесь

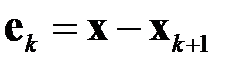(6.9)

вектор ошибки, представляющий отклонение 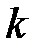-го приближения от точного решения.

Очевидно, что последовательность сходится к точному решению в том случае, если последовательность векторов ошибки 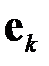сходится к нулевому вектору. Известно [5.1], что последовательность 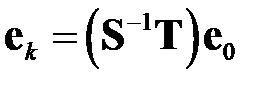сходится к нулевому вектору тогда и только тогда, когда все собственные значения матрицы 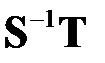имеют модуль меньше единицы:

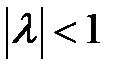. (6.10)

То, что методы Якоби и Гаусса-Зейделя могут сходиться медленно, объясняется тем, что максимальное собственное значение матрицы 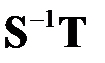для решаемой задачи оказывается близко по модулю к 1.

Если же окажется, что 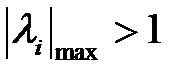, то итерационный метод будет расходиться.

Определение собственных значений само по себе является довольно сложной математической задачей. Тем более сложно придумать рецепт – как расщеплять матрицу для любой системы .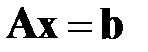

Тем не менее, в 1950г. [5.2] был найден очень хороший способ расщепления матриц, который, во всяком случае, обеспечивает быструю сходимость для симметричных положительно определенных матриц.

Идею метода можно наглядно пояснить следующим образом. Еще во времена, когда вычисления производились вручную, было замечено, что при применении метода Гаусса-Зейделя итерации сходятся монотонно. Можно сказать, что «приближения остаются с одной и той же стороны от решения x» [5.1].

Последнюю фразу несколько трудно понять применительно к вектору хпроизвольной размерности. Однако можно проиллюстрировать схемой для известных итерационных методов для уравнения 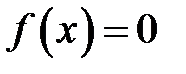(см рис.6.1).

Любой итерационный метод фактически состоит в том, что некоторое 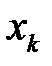приближение уточняется с использованием некоторой поправки :

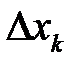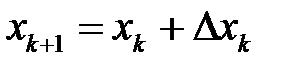(6.11)

Для разных методов способ этой поправки может быть свой. Но в любом случае очередное приближение может быть записано в виде (6.11).

x

f

x

а) метод хорд

б) метод касательных

Рис.6.1

По рис.6.1 можно сделать наблюдение, что если поправку принимать немного больше, чем это предлагает итерационный метод, то, возможно, сходимость итерационного процесса окажется быстрее. То есть, если вместо (6.11) использовать

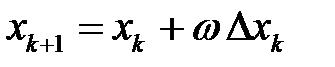, (6.12)

где 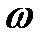‑ некоторое число, большее 1.

В упомянутой диссертации Янга эта идея распространена на системы линейных уравнений. Итерационная формула, аналогичная (6.4), при этом принимает вид [6.3]:

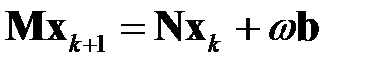(6.13)

где

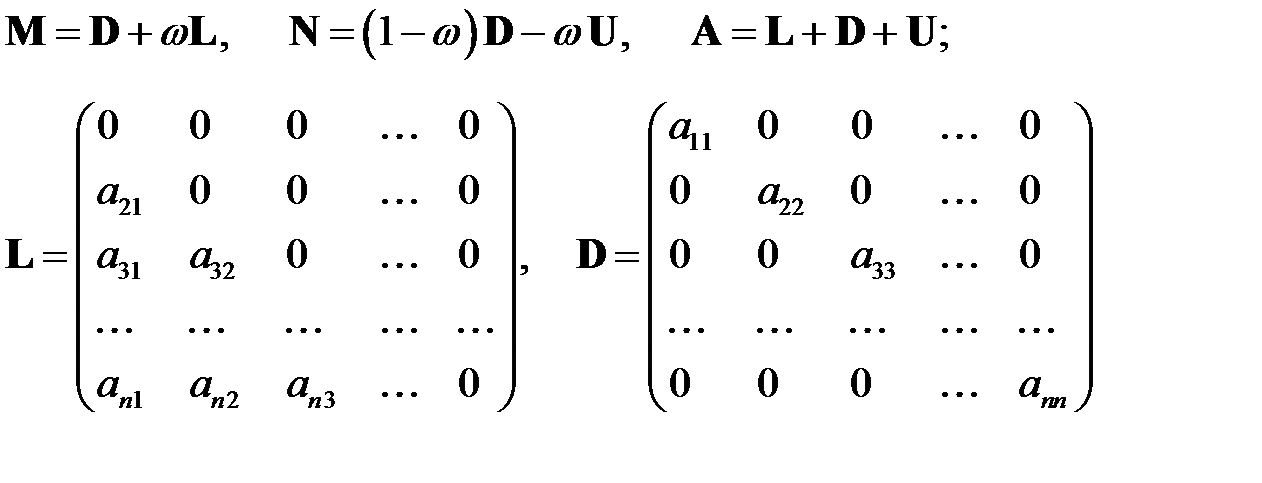(6.14)

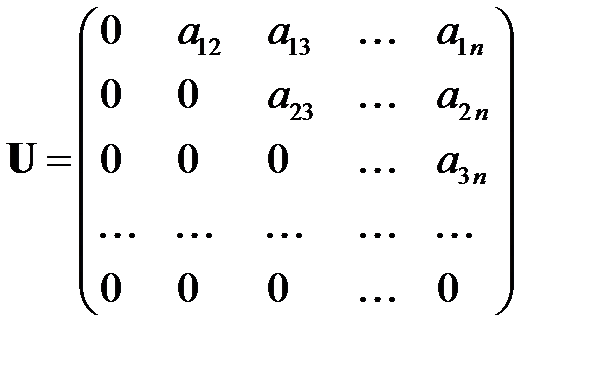
Остается вопрос, какое значение следует принять для 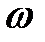? В общем случае это достаточно сложная проблема. Но, во всяком случае, известно, что это число должно быть больше 1, но меньше 2. При 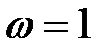(6.13) превращается в метод Гаусса-Зейделя. При 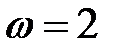не выполняется условие сходимости (6.10).

Обычно хорошим выбором является 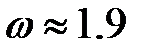. Но для различных классов систем линейных уравнений оптимальный выбор 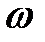является самостоятельной и довольно сложной задачей.

Литература

6.1. Стренг Г. Линейная алгебра и ее применения. – М.: Мир, 1980. – 454с.

6.2. Young D.M. – Iterative Methods for Solving Partial Difference Equations of Elliptic Type. Doctoral thesis. – Harvard University, 1950.

6.3. Голуб Дж., Ван Лоун Ч. Матричные вычисления. – М.: Мир, 1999. – 548 с.