Краткие теоретические сведения. Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины

Тема 1. Линейная алгебра

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины.

Матрица записывается в виде 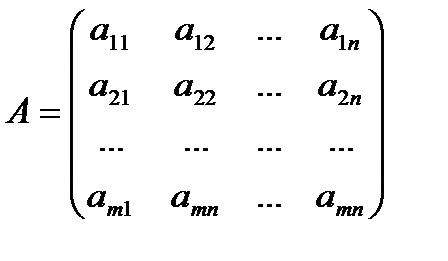или, сокращенно, 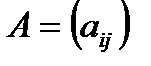, где i = 1, 2, 3, … , m – номер строки, j = 1, 2, 3, … , n – номер столбца.

Матрицу A называют матрицей размера m×n и записывают как A .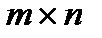

Числа 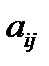, составляющие матрицу, называются ее элементами.

Матрица, у которой число строк равно числу столбцов называют квадратной.

Квадратную матрицу размера n×n называют матрицей n- го порядка.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Элементы 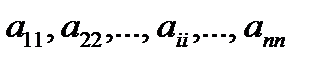образуют главную диагональ квадратной матрицы A

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Единичная матрица обозначается буквой E.

Матрица, полученная из данной матрицы заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной матрице. Обозначается .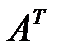

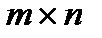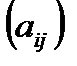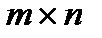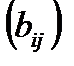Суммой двух матриц A = и B = называется матрица C 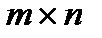= 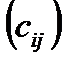такая, что 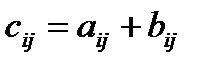(i = 1, 2, … , m; j = 1, 2, … , n).

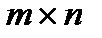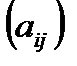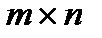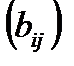Разностью двух матриц A = и B = называется матрица C 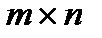= 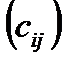такая, что 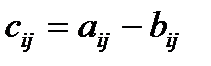(i = 1, 2, … , m; j = 1, 2, … , n).

Произведением матрицы A 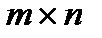= 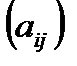на число k называется матрица B 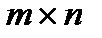= 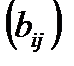такая, что 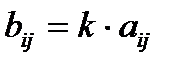(i = 1, 2, … , m; j = 1, 2, … , n).

Произведением матрицы A 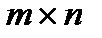= 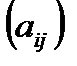на матрицу B 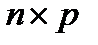= 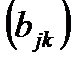называется матрица C 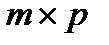= 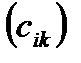такая, что (i = 1, 2, … , m; k = 1, 2, … , p).

Определителем квадратной матрицы второго порядка A = 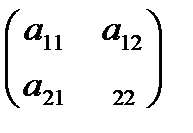называется число = .

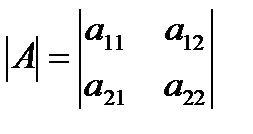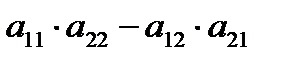Определителем квадратной матрицы третьего порядка A = 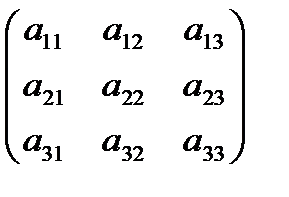называется число = = .

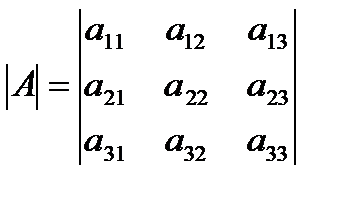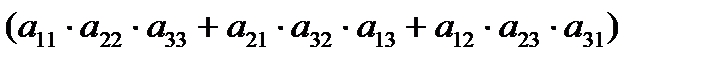
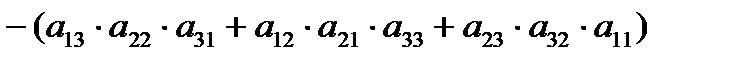Минором элемента 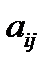определителя n-го порядка называется определитель n-1-гопорядка, полученный из исходного определителя вычеркиванием i – той строки и j-го столбца.Обозначается минор элемента : .

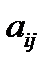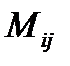Алгебраическим дополнением элемента 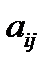определителя называется число .

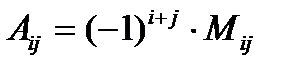Матрицей, союзной к матрице A, называется матрица

= ,

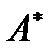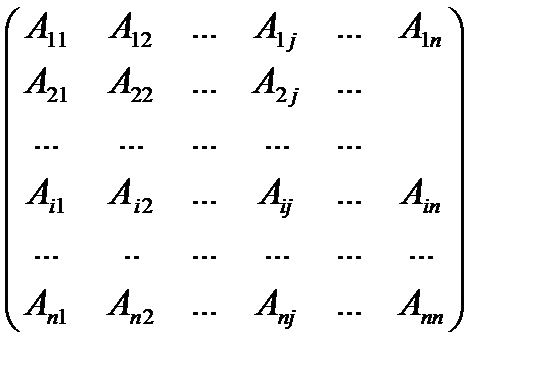где 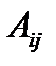– алгебраические дополнения элементов 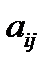определителя матрицы A.

Матрица 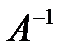называется обратной к матрице A, есливыполняется условие: 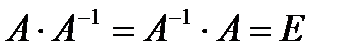, где E – единичная матрица того же порядка, что и матрица A.

Обратная матрица к матрице A, находится по формул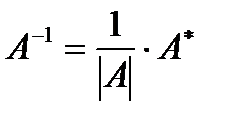е: , где 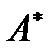- матрица, союзная к транспонированной матрице .

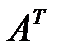Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида

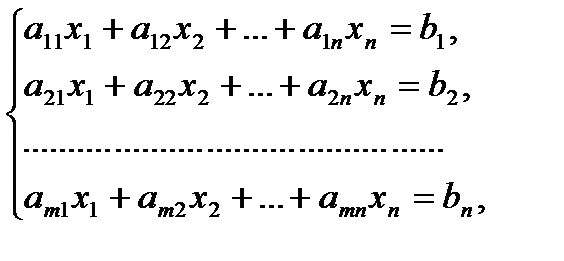(1)

где 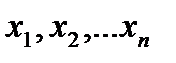- неизвестные, числа 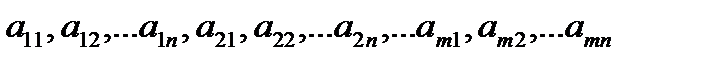- коэффициенты системы, 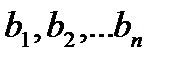- свободные члены.

Матрица 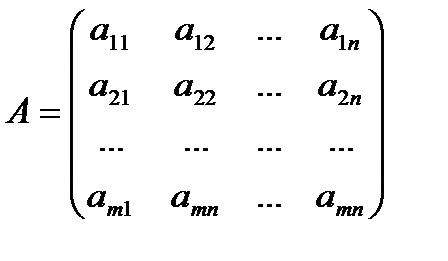называется основной матрицей системы линейных уравнений (1).

Матрица 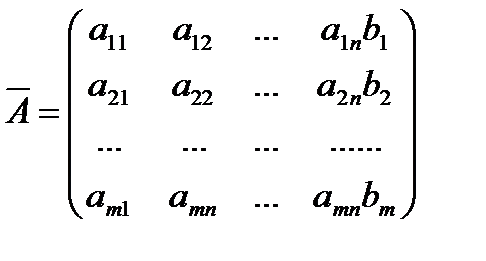называется расширенной матрицей системы линейных уравнений (1).

Решением системы (1) называется n значений неизвестных 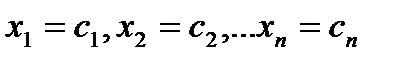, при подстановке которых в систему (1) каждое уравнение системы обращается в верное равенство.

Система уравнений называется совместной, если она имеет хотя бы одно решение.

Система уравнений называется несовместной, если она не имеет ни одного решения.

Совместная система уравнений называется определенной, если она имеет единственное решение.

Совместная система уравнений называется неопределенной, если она имеет более одного решения.

Решить систему уравнений – это значит выяснить, совместна она или несовместна.

Две системы уравнений называются равносильными, если они имеют одно и то же множество решений.

Равносильные системы линейных уравнений получаются при элементарных преобразованиях системы.

К элементарным преобразованиям системы линейных уравнений относятся:

- перестановка местами двух уравнений системы;

- умножение уравнения системы на ненулевое число;

- замена какого-то уравнения системы на сумму этого уравнения и другого уравнения системы, умноженного на какое-то число;

- удаление из системы линейных уравнений уравнения вида 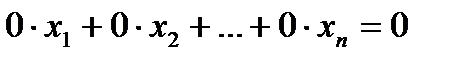.