Кручение прямого стержня круглого поперечного сечения
СДВИГ И КРУЧЕНИЕ
Расчет элементов конструкций, работающих на сдвиг
Если из всех внутренних сил не равна нулю только поперечная сила, материал испытывает сдвиг. На сдвиг работают шпонки, штифты, заклепочные, сварные, и другие соединения. При действии нагрузки в этих соединениях, кроме сдвига, возникает смятие и изгиб. Такое явление на практике называется срезом. Экспериментально доказано, что напряжения при сдвиге равномерно распределяются по площади. Рассмотрим расчет некоторых соединений.
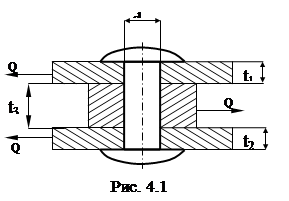 Расчет заклепочных соединений ( рис.4.1 ). Из условия прочности при сдвиге:
Расчет заклепочных соединений ( рис.4.1 ). Из условия прочности при сдвиге:
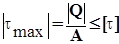
получим 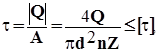
где: 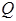 – поперечная сила;
– поперечная сила; 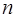 – число срезов;
– число срезов; 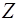 – число заклепок, можно подобрать либо диаметр заклепки, либо число заклепок, которое округляется до ближайшего большего целого числа:
– число заклепок, можно подобрать либо диаметр заклепки, либо число заклепок, которое округляется до ближайшего большего целого числа:
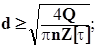
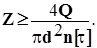
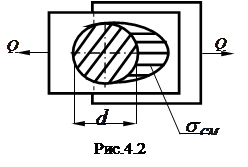 Кроме сдвига заклепочные соединения рассчитываются на смятие. Реальное распределение напряжений смятия имеет сложный вид ( рис. 4.2 ). Поэтому для расчетов эпюру напряжений,
Кроме сдвига заклепочные соединения рассчитываются на смятие. Реальное распределение напряжений смятия имеет сложный вид ( рис. 4.2 ). Поэтому для расчетов эпюру напряжений, 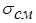 упрощают и заменяют постоянной величиной, а за площадь смятия прини-мают диаметральное сечение заклепки.
упрощают и заменяют постоянной величиной, а за площадь смятия прини-мают диаметральное сечение заклепки.
Тогда, из условий прочности при смятии
для крайних листов 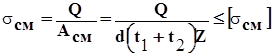
и для среднего листа 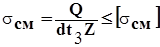
можно определить либо диаметр заклепок, либо их число.
Например, для крайних листов 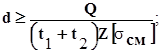
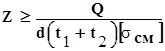 .
.
Число заклепок округляют до ближайшего большего целого числа.
В общем случае расчет на смятие проводят как для заклепок, так и для листов. При этом, если они из разных материалов, то будут разные 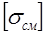 . Обычно
. Обычно 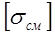 велико, вследствие того, что в возникающем объемном напряженном состоянии все напряжения практически всегда отрицательны. Окончательно, из результатов всех расчетов, принимают для соединения наибольшие значения диаметров или числа заклепок.
велико, вследствие того, что в возникающем объемном напряженном состоянии все напряжения практически всегда отрицательны. Окончательно, из результатов всех расчетов, принимают для соединения наибольшие значения диаметров или числа заклепок.
Расчет сварных соединений
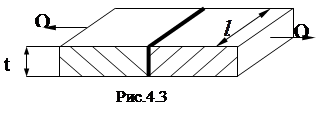 Соединение встык ( рис. 4.3 ).
Соединение встык ( рис. 4.3 ).
Из условия прочности
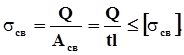 ,
,
можно найти длину сварного шва
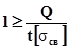 . Из-за непровара по краям шва, его длину увеличивают на
. Из-за непровара по краям шва, его длину увеличивают на 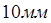 .
.
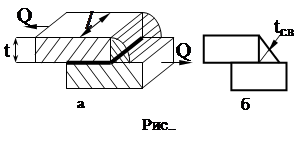
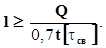 Соединение внахлест ( рис. 4.4,а ). Наименьшая толщина шва показана на рис.4.4,б
Соединение внахлест ( рис. 4.4,а ). Наименьшая толщина шва показана на рис.4.4,б 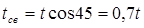 . Тогда из условия прочности
. Тогда из условия прочности 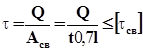 находим длину сварного шва
находим длину сварного шва
 а затем увеличиваем ее на
а затем увеличиваем ее на 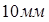 .
.
Здесь 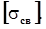 и
и 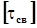 - допускаемые напряжения для сварных соединений.
- допускаемые напряжения для сварных соединений.
4.2. Чистый сдвиг
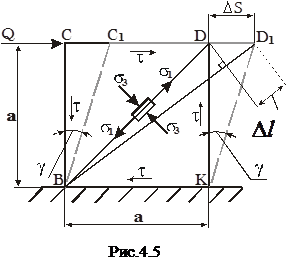 Если по граням элемента действуют только касательные напряжения, то материал элемента испытывает деформацию чистого сдвига. Рассмотрим некоторое тело единичной толщины ( рис.4.5 ). На грани CD под действием силы Q возникают касательные напряжения
Если по граням элемента действуют только касательные напряжения, то материал элемента испытывает деформацию чистого сдвига. Рассмотрим некоторое тело единичной толщины ( рис.4.5 ). На грани CD под действием силы Q возникают касательные напряжения
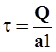 .
.
По закону парности касатель-ных напряжений, такие же напря-жения возникают на остальных гранях тела. От действия τ верхняя грань CD переместится в положение C1D1, сдвинувшись на величину DD1, равную
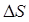 , называемую абсолютным сдвигом. Все прямые углы элемента станут тупыми и острыми, изменившись на величину g , называемую углом сдвига.
, называемую абсолютным сдвигом. Все прямые углы элемента станут тупыми и острыми, изменившись на величину g , называемую углом сдвига. 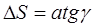 . Так как угол g мал, то
. Так как угол g мал, то 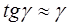 и
и 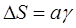 .
.
Рассмотрим деформацию диагонали 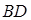 c двух точек зрения.
c двух точек зрения.
С геометрической точки зрения. Свяжем удлинение диагонали BD и абсолютный сдвиг. Считаем, что 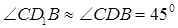 .Тогда
.Тогда 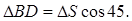 Деформация диагонали
Деформация диагонали 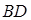 будет
будет
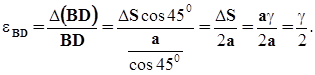
С точки зрения напряженного состояния. Рассматриваемый элемент испытывает плоское напряженное состояние. Определим положение главных площадок по формуле ( 3.8 ) .
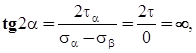 откуда
откуда 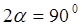 и
и 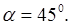
Таким образом, главные площадки расположены под углом 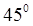 к заданным. Найдем величины главных напряжений по формулам ( 3.9 )
к заданным. Найдем величины главных напряжений по формулам ( 3.9 )
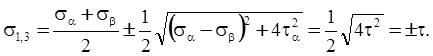 s 2 = 0.
s 2 = 0.
При чистом сдвиге главные напряжения равны по величине и противоположны по знаку. Для определения деформации диагонали BD используем обобщенный закон Гука ( 3.10 )
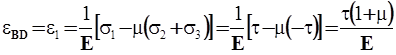 . Приравняем значения:
. Приравняем значения:
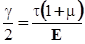 , откуда следует, что
, откуда следует, что 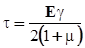 . Обозначим
. Обозначим 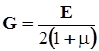 .
.
Упругая постоянная G называется модулем сдвига, или модулем поперечной упругости, или модулем упругости второго рода. Из последней формулы следует, что упругие характеристики материала G , E и m связаны между собой. Тогда закон Гука при сдвиге запишется
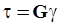 . ( 4.1 )
. ( 4.1 )
Найдем потенциальную энергию деформации при сдвиге. Площадь верхней грани тела ( рис.4.5 ) равна 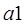 . Сдвигающиеся сила
. Сдвигающиеся сила 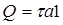 . Потенциальная энергия деформации данного элемента
. Потенциальная энергия деформации данного элемента 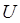 равна работе
равна работе 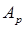 внешней силы на перемещении
внешней силы на перемещении 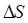
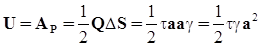 .
.
Разделив полученную величину на объем V = aа1 тела, найдем удельную потенциальную энергию деформации 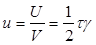 . Из выражения ( 4.1 ) получим
. Из выражения ( 4.1 ) получим 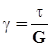 . Тогда
. Тогда 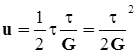 . ( 4.2 )
. ( 4.2 )
Кручение прямого стержня круглого поперечного сечения
Стержень, работающий на кручение, называется валом. При кручении в поперечном сечении вала возникает одно внутреннее усилие - крутящий момент 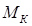 .
. 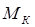 определяют на каждом участке вала с помощью метода сечений.
определяют на каждом участке вала с помощью метода сечений. 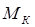 равен алгебраической сумме всех закручивающих моментов, взятых по одну или по другую сторону от сечения. При этом, если смотреть со стороны сечения на рассматриваемую часть вала, то закручивающий момент, вращающий против часовой стрелки, считается положительным.
равен алгебраической сумме всех закручивающих моментов, взятых по одну или по другую сторону от сечения. При этом, если смотреть со стороны сечения на рассматриваемую часть вала, то закручивающий момент, вращающий против часовой стрелки, считается положительным.
Введем следующие допущения, подкрепленные экспериментально для валов круглого и кольцевого поперечных сечений:
1.Плоские поперечные сечения вала, перпендикулярные его оси до кручения, остаются плоскими и перпендикулярными оси во время кручения, поворачиваясь относительно друг друга на некоторый угол.
2.Прямые радиусы, проведенные в этих сечениях, остаются прямыми при кручении.
3. Расстояние между сечениями во время кручения не меняется.
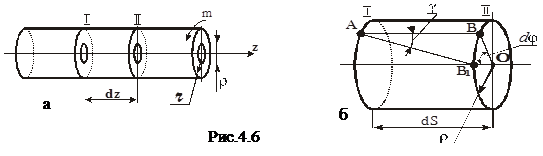
Рассмотрим вал, находящийся в состоянии кручения. ( рис.4.6,а ). Проведем два плоских сечения, перпендикулярных оси вала, и расположенных на расстоянии 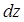 друг от друга. Во время кручения второе сечение ( рис.4.6,б ) повернется относительно первого, и образующая
друг от друга. Во время кручения второе сечение ( рис.4.6,б ) повернется относительно первого, и образующая 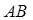 займет положение
займет положение 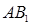 . Радиус повернется на некоторый угол
. Радиус повернется на некоторый угол 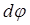 и примет положение
и примет положение 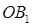 . Из
. Из 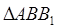 :
: 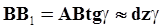 .
.
Из треугольника 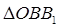 :
: 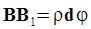 . Поэтому
. Поэтому 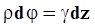 , или
, или 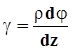 .
.
 |
Обозначим 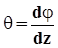 - относительный угол закручивания. Тогда
- относительный угол закручивания. Тогда 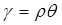 .
.
Из ( рис. 4.6,б ) видно, что материал при кручении испытывает деформацию сдвига, и по закону Гука при сдвиге касательные напряжения равны.

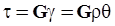 . ( 4.3 )
. ( 4.3 )
Рассмотрим поперечное сечение вала ( рис. 4.7 ). Выделим площадку 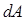 . Здесь
. Здесь 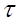 перпендикулярно
перпендикулярно 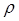 . Тогда элементарный крутящий момент будет:
. Тогда элементарный крутящий момент будет: 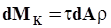 .
.
Полный крутящий момент
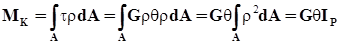 .
.
Отсюда находим относительный угол закручивания 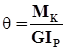 .
.
 Подставляем его в ( 5.3 ) и получим формулу для определения касательных напряжений в сечении вала при кручении :
Подставляем его в ( 5.3 ) и получим формулу для определения касательных напряжений в сечении вала при кручении :
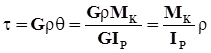 . ( 4.4 )
. ( 4.4 )
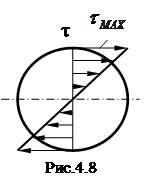
Максимальное касательное напряжение 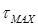 возникают при
возникают при 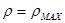 ( рис. 4.8 )
( рис. 4.8 )
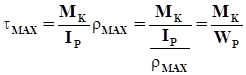 . ( 4.5 )
. ( 4.5 )
Запишем условие прочности: 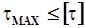 .
. 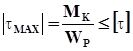 .
.
Из условия прочности находим формулу для подбора размера поперечного сечения вала: 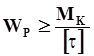 . ( 4.6 )
. ( 4.6 )
Для круглого поперечного сечения : 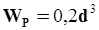 ,
, 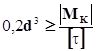 ,
, 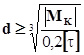 .
.
Определим перемещение при кручении.
Подставим 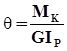 в
в 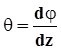 . Тогда
. Тогда 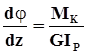 , и
, и 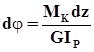
Угол закручивания участка вала длиной ℓ будет: 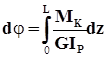 .
.
Обычно вал делится на участки, на которых 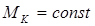 и жесткость вала
и жесткость вала 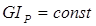 , тогда
, тогда
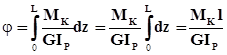 . ( 4.7 )
. ( 4.7 )
В некоторых конструкциях необходимо, чтобы угол закручивания не превышал допустимый угол закручивания 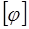 . Тогда из условия жесткости
. Тогда из условия жесткости
вала 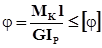 , получим
, получим 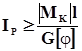 .
.
Для вала круглого поперечного сечения
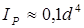 ,
, 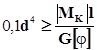 ,
, 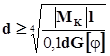 .
.
