Веса результатов измерений и их функций

Вес результата измерения определяют по формуле

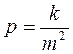, (3.11)

где 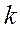– произвольно выбранное число одинаковое для всех весов, участвующих в решении задачи;

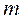– СКП результата измерения.

Вес – относительная характеристика точности, т.е. он дает представление о точности результата измерения только при сравнении с весами других результатов измерений в данной задаче.

В качестве единицы меры дисперсий принимают СКП измерения 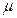, вес которой равен единице (СКП единицы веса).

Подставив в (3.11) вместо 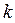величину 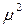, получим

,

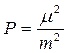откуда

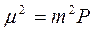
или

,

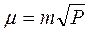а

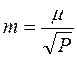. (3.12)

Величину 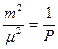называют обратным весом.

Заменив в формуле (3.6) величины 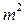на обратные веса, получаем формулу для вычисления веса функции измеренных величин

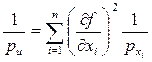. (3.13)

Таким образом, методика определения весов функций измеренных величин такая же, что и при вычислении СКП функций измеренных величин. Формулы для определения весов функций получаются из формул для СКП тех же функций заменой величин 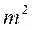соответствующими им обратным весом .

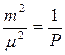Порядок вычисления веса функции измеренных величин следующий:

1) записывается функция в буквенном выражении;

2) определяется обратный вес этой функции по вышеизложенным правилам;

3) осуществляется переход от обратного веса к весу.

Решение задач

Пример 8.

Измерены два угла с СКП, соответственно равными 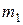= 5² и 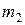= 1². Вычислить веса этих результатов измерений, если .

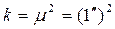Решение.

Веса заданных величин будут

;

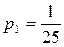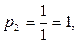
а в качестве величины, обладающей единичным весом, выступает угол, точность измерения которого характеризуется СКП равной 1².

Пример 9.

Вычислить вес дирекционного угла 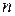- ой линии хода при условии равноточности результатов измерения углов хода и безошибочности дирекционного угла исходной стороны.

Решение.

Дирекционный угол последней линии теодолитного хода вычисляем по известной формуле

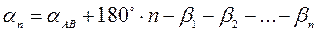
Условие равноточности измерения углов хода требует дать всем измеренным значениям углов один и тот же вес, в частности, равный единице, т.е. .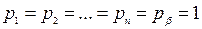

Тогда на основании формулы (3.17) записываем выражение обратного веса дирекционного угла последней линии хода. Необходимо учесть, что слагаемое 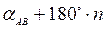в предыдущей формуле принимается как безошибочная величина с нулевой дисперсией, и, следовательно, с нулевым обратным весом. На основании этого имеем

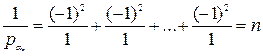
Тогда .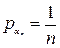

Пример 10.

С плана графически сняты прямоугольные координаты 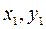начала и 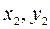конца некоторого отрезка, после чего была вычислена его длина 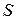. Принимая, что все четыре координаты были получены равноточно, вычислить вес длины этого отрезка. Сравнить полученное значение веса с весом значения непосредственного измерения линии по карте, если такое измерение выполняется с той же точностью, что и измерение любой из координат конца отрезка.

Решение.

Длина 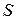определяется соотношением

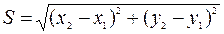
Учитывая, что все четыре координаты получены равноточно, то им можно приписать одинаковый вес, т.е. записать, что .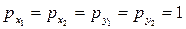

Величина 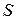является нелинейной функцией координат, и для решения поставленной задачи необходимо вычислить частные производные 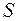по всем координатам. Они имеют вид:

.

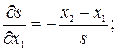
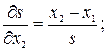
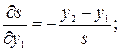
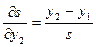Подставляя значения частных производных в формулу обратного веса, получим

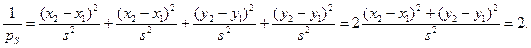
Следовательно,

.

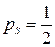Если принять, что измерение отрезка по карте выполняется с той же точностью, что и измерение любой координаты, то приходим к выводу, что получение длины 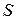непосредственно с плана будет иметь вес равный единице, т. е. в два раза больший, чем ее косвенное вычисление через измеренные координаты.

Задача 16.

Веса результатов измерений горизонтальных углов равны 0,5; 1,0; 1,5; 2,0 соответственно. Вычислить их СКП, если известно, что СКП единицы веса 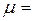...... (см. приложение табл. 2).

Указание: при решении задачи воспользоваться формулой (3.12), связывающей Р, m, μ.

Задача 17.

Найти вес невязки в сумме углов треугольника, если все углы измерены равноточно.

Задача 18.

Чему равен вес среднеарифметического значения угла, полученного из 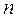=.... приемов (см. приложение табл. 2)?

Задача 19.

Определить вес площади прямоугольного треугольника, если катеты: а = 50 м и b = 80 м измерены с весами , .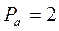

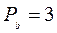Задача 20.

Определить вес гипотенузы прямоугольного треугольника, вычисленной по измеренным катетам: а = 60 м и b = 80 м, есл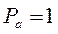и и .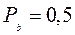

Задача 21.

В треугольнике один угол получен 3 приемами, второй — 9, а третий — вычислен. Найти вес третьего угла, приняв вес измеренного одним приемом угла за единицу.

Задача 22.

Чему равен вес угла, измеренного тремя приемами, если вес угла, измеренного одним приемом, равен 1.