Необходимая численность выборки
Разрабатывая программу выборочного наблюдения, задаются конкретным значением предельной ошибки и уровнем вероятности. Неизвестной остается минимальная численность выборки, обеспечивающая заданную точность. Ее можно получить из формул средней и предельной ошибок в зависимости от типа выборки. Так, подставляя формулы сначала (65) и затем (66) в формулу (67) и решая ее относительно численности выборки, получим следующие формулы:
для повторной выборки n =  ; (72) для бесповторной выборки n =
; (72) для бесповторной выборки n =  . (73)
. (73)
Вариация ( 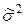 ) значений признака к началу выборочного наблюдения как правило неизвестна, поэтому ее берут приближенно одним из способов:
) значений признака к началу выборочного наблюдения как правило неизвестна, поэтому ее берут приближенно одним из способов:
1) берется из предыдущих выборочных наблюдений;
2) по правилу «трех сигм», согласно которому в размахе вариации укладывается примерно 6 стандартных отклонений  (H/
(H/  = 6, отсюда
= 6, отсюда 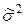 = Н2 /36);
= Н2 /36);
3) если приблизительно известна средняя величина изучаемого признака, то 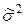 =
= 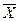 2 /9;
2 /9;
4) если неизвестна дисперсия доли единиц, обладающих каким-либо значением признака, то используется ее максимально возможная величина 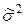 = 0,25.
= 0,25.
Методические указания
Задача. На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за месяц (таблица 24):
Таблица 24. Результаты бесповторного выборочного наблюдения на предприятии
| Доход, у.е. | до 300 | 300-500 | 500-700 | 700-1000 | более 1000 |
| Число рабочих |
С вероятностью 0,950 определить:
1) среднемесячный размер дохода работников данного предприятия;
2) долю рабочих предприятия, имеющих месячный доход более 700 у.е.;
3) необходимую численность выборки при определении среднемесячного дохода работников предприятия, чтобы не ошибиться более чем на 50 у.е.;
4) необходимую численность выборки при определении доли рабочих с размером месячного дохода более 700 у.е., чтобы при этом не ошибиться более чем на 5%.
Решение. Для расчета обобщающих характеристик выборки построим вспомогательную таблицу 25.
Таблица 25. Вспомогательные расчеты для решения задачи
| X | f | Х’ | X’f | (Х’ - 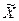 )2 )2 | (Х’ - 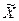 )2f )2f |
| до 300 | |||||
| 300 - 500 | |||||
| 500 - 700 | |||||
| 700 - 1000 | |||||
| более 1000 | |||||
| Итого |
По формуле (11) рассчитаем средний доход в выборке: 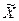 = 57100/100 = 571 (у.е.). Применив формулу (28) и рассчитав ее числитель в последнем столбце таблицы, получим дисперсию среднего выборочного дохода:
= 57100/100 = 571 (у.е.). Применив формулу (28) и рассчитав ее числитель в последнем столбце таблицы, получим дисперсию среднего выборочного дохода: 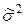 = 4285900/100 = 42859.
= 4285900/100 = 42859.
Теперь можно определить среднюю ошибку выборки по формуле (66): 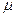 =
=  = 19,640 (у.е.).
= 19,640 (у.е.).
В нашей задаче  = 0,950, значит t = 1,96. Тогда предельная ошибка выборки по формуле (67):
= 0,950, значит t = 1,96. Тогда предельная ошибка выборки по формуле (67):
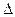 = 1,96*19,64 = 38,494 (у.е.).
= 1,96*19,64 = 38,494 (у.е.).
Для определения средней ошибки выборки при определении доли рабочих с доходами более 700 у.е. в ГС необходимо определить их долю: w = 20/100 = 0,2 или 20%, а затем ее дисперсию по формуле 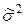 = w(1-w) = 0,2*(1–0,2) = 0,16. Тогда можно рассчитать среднюю ошибку выборки по формуле (66):
= w(1-w) = 0,2*(1–0,2) = 0,16. Тогда можно рассчитать среднюю ошибку выборки по формуле (66): 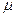 =
=  = 0,038 или 3,8%. А затем и предельную ошибку выборки по формуле (67):
= 0,038 или 3,8%. А затем и предельную ошибку выборки по формуле (67):
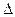 = 1,96*0,038 = 0,075 или 7,5%.
= 1,96*0,038 = 0,075 или 7,5%.
Доверительный интервал среднего дохода находим по формуле (70):
571-38,494 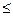
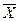
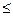 571+38,494 или 532,506 у.е.
571+38,494 или 532,506 у.е. 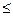
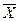
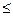 609,494 у.е., то есть средний доход всех рабочих предприятия с вероятностью 95% будет лежать в пределах от 532,5 до 609,5 у.е.
609,494 у.е., то есть средний доход всех рабочих предприятия с вероятностью 95% будет лежать в пределах от 532,5 до 609,5 у.е.
Аналогично определяем доверительный интервал для доли по формуле (71):
0,2-0,075 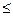 p
p 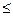 0,2+0,075 или 0,125
0,2+0,075 или 0,125 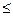 p
p 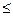 0,275, то есть доля рабочих с доходами более 700 у.е. на всем предприятии с вероятностью 95% будет лежать в пределах от 12,5% до 27,5%.
0,275, то есть доля рабочих с доходами более 700 у.е. на всем предприятии с вероятностью 95% будет лежать в пределах от 12,5% до 27,5%.
В нашей задаче выборка бесповторная, значит, воспользуемся формулой (73), в которую подставим уже рассчитанные дисперсии среднего выборочного дохода рабочих ( 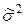 = 42859) и доли рабочих с доходами более 700 у.е. (
= 42859) и доли рабочих с доходами более 700 у.е. ( 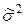 = 0,16):
= 0,16):
nб/повт =  = 62 (чел.), nб/повт=
= 62 (чел.), nб/повт=  = 197 (чел.).
= 197 (чел.).
Таким образом, необходимо включить в выборку не менее 62 рабочих при определении среднего месячного дохода работников предприятия, чтобы не ошибиться более чем на 50 у.е., и не менее 197 рабочих при определении доли рабочих с размером месячного дохода более 700 у.е., чтобы при этом не ошибиться более чем на 5%.
Контрольные задания
Для изучения вкладов населения в коммерческом банке города была проведена 5%-я случайная бесповторная выборка лицевых счетов, в результате которой в таблице 26 получено распределение клиентов по размеру вкладов.
Таблица 26. Варианты выполнения контрольного задания
| Размер вклада, у.е. | Число вкладчиков, чел. | |||||||||
| Вариант | ||||||||||
| до 5000 | ||||||||||
| 5 000 – 15 000 | ||||||||||
| 15 000 – 30 000 | ||||||||||
| 30 000 – 50 000 | ||||||||||
| свыше 50 000 |
С вероятностью 0,954 определить:
1) средний размер вклада во всем банке;
2) долю вкладчиков во всем банке с размером вклада свыше 15000 у.е.;
3) необходимую численность выборки при определении среднего размера вклада, чтобы не ошибиться более чем на 500 у.е.;
4) необходимую численность выборки при определении доли вкладчиков во всем банке с размером вклада свыше 30 000 у.е., чтобы не ошибиться более чем на 10%.
Ряды динамики
Понятие о рядах динамики
Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).
Ряд динамики – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).
Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают через y. Первый член ряда y1 называют начальным (базисным) уровнем, а последний yn – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.
Ряды динамики, как правило, представляют в виде таблицы (см. табл. 27) или графически (см. рис. 13), причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.
Таблица 27. Внешнеторговый оборот (ВО) России за период 2000-2006 гг.
| Год | |||||||
| Млрд. долл. США | 149,9 | 155,6 | 168,3 | 212,0 | 280,6 | 368,9 | 468,4 |

Рис. 13. Внешнеторговый оборот (ВО) России за период 2000-2006 гг.
Данные табл. 27 и рис. 13 наглядно иллюстрируют ежегодный рост внешнеторгового оборота (ВО) в России за период 2000-2006 гг.
