Геометрические преобразования графиков функции
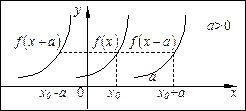 |
Если известен график функции 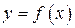 , то с помощью некоторых преобразований можно построить графики более сложных функций.
, то с помощью некоторых преобразований можно построить графики более сложных функций.
1. График функции 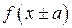 получается параллельным переносом графика
получается параллельным переносом графика 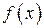 вдоль оси
вдоль оси 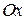 на
на 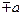 .
.
Значение функции 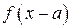 при
при 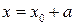 совпадает со значением
совпадает со значением 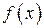 при
при 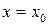 .
.
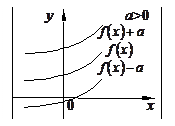 2. График функции
2. График функции 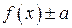 получается параллельным переносом графика функции
получается параллельным переносом графика функции 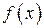 вдоль оси
вдоль оси 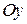 на
на 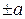 .
.
3. График функции 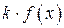 получается растяжением графика
получается растяжением графика 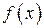 вдоль оси
вдоль оси 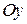 в
в 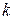
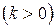 раз при
раз при 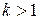 и сжатием вдоль этой оси в
и сжатием вдоль этой оси в 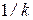 раз при
раз при 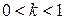 ; если
; если 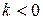 , то к этому преобразованию добавляется зеркальное отражение относительно оси
, то к этому преобразованию добавляется зеркальное отражение относительно оси 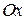 .
.
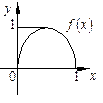
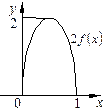
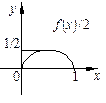
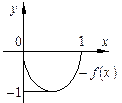
4. График функции 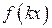 получается сжатием графика
получается сжатием графика 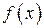 вдоль оси
вдоль оси 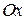 в
в 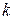
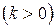 раз при
раз при 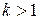 и растяжением вдоль этой же оси в
и растяжением вдоль этой же оси в 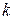 раз при
раз при 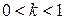 ; если
; если 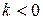 , то к этому преобразованию добавляется зеркальное отражение относительно оси
, то к этому преобразованию добавляется зеркальное отражение относительно оси 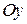 .
.
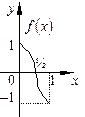
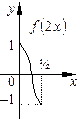
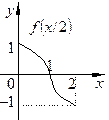
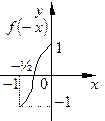
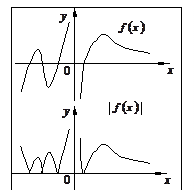 5. График функции
5. График функции 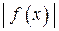 получается из графика функции
получается из графика функции 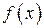 следующим преобразованием: часть графика, лежащая выше оси
следующим преобразованием: часть графика, лежащая выше оси 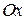 , остается на месте; часть графика, лежащая ниже оси
, остается на месте; часть графика, лежащая ниже оси 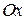 , зеркально отражается относительно оси
, зеркально отражается относительно оси 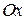 .
.
6. График функции 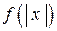 получается из графика
получается из графика 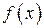 следующим преобразованием: при
следующим преобразованием: при 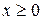 график не изменяется; при
график не изменяется; при 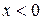 график заменяется на
график заменяется на
зеркальнoе отражение относительно оси 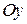 части графика, соответствующей
части графика, соответствующей 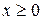 .
.


| пп 10. Теоретические Упражнения | ||
| ТУ ПП 10. №1. | Пользуясь стандартными символами, запишите определения четности, нечетности, периодичности, ограниченности и монотонности функций. | |
| ТУ ПП 10. №2. | Приведите пример неограниченной функции, непрерывной на интервале. РЕШЕНИЕ:  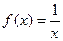 непрерывна на интервале (0, 1),ноне ограничена. непрерывна на интервале (0, 1),ноне ограничена. |
| ТУ ПП 10. №3. | Справедливо ли утверждение о том, что непрерывная на 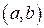 функция достигает на нем своих точной верхней и точной нижней граней? РЕШЕНИЕ: Для функция достигает на нем своих точной верхней и точной нижней граней? РЕШЕНИЕ: Для 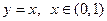 , значения , значения 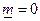 и и 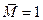 - не достигаются на интервале - не достигаются на интервале 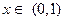 . . | нет |
| ТУ ПП 10. №4. | Покажите, что функция y = x2 непрерывна в произвольной точке x0 вещественной оси. РЕШЕНИЕ: Действительно, числовые значения f(x0) = x02 и f(x0 + Dx) = (x0 + Dx)2 порождают приращение функции вида Dy = (x0 + Dx)2 – x02 = x02 + 2x0 × Dx + Dx2 – x02 = 2x0 × Dx + Dx2. Используя 2-е определение непрерывности, имеем 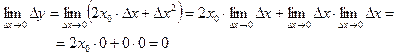 Поскольку 2-е определение выполняется, функция непрерывна. Поскольку 2-е определение выполняется, функция непрерывна. | |
| ТУ ПП 10. №5. | Покажите, что функция y = sin x непрерывна в произвольной точке x0 вещественной оси. РЕШЕНИЕ: Действительно, числовые значения f(x0) = sin x0 и f(x0+Dx) = sin(x0+Dx) порождают приращение функции вида Dy = sin(x0 + Dx) - sinx0 = 2sin(Dx/2)×cos(x0 + Dx/2). В теории пределов было доказано, что 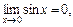 поэтому поэтому 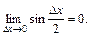 Используя 2-е определение непрерывности, имеем: Используя 2-е определение непрерывности, имеем: 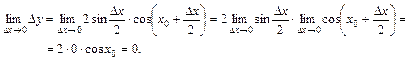 Поскольку 2-е определение выполняется, функция непрерывна. Поскольку 2-е определение выполняется, функция непрерывна. |
| ТУ ПП 10. №6. | Докажите, что 2-е определение непрерывности равносильно 1-му определению. РЕШЕНИЕ: Используя арифметические свойства предела, получаем 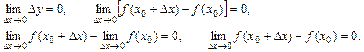 По определению приращения Dx = x – x0, поэтому По определению приращения Dx = x – x0, поэтому 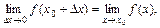 и тем самым и тем самым 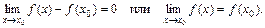 Последнее равенство и означает 1-е определение непрерывности. Последнее равенство и означает 1-е определение непрерывности. | |
| ТУ ПП 10. №7. | Покажите, что 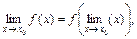 т.е. знак непрерывной в точке x0 функции y = f(x) и знак предела перестановочны. Вычислите предел: т.е. знак непрерывной в точке x0 функции y = f(x) и знак предела перестановочны. Вычислите предел: 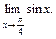 РЕШЕНИЕ: РЕШЕНИЕ: 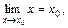 поэтому 1-е определение непрерывности может быть записано в виде поэтому 1-е определение непрерывности может быть записано в виде 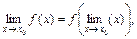 Функция y = sinx непрерывна в любой точке, поэтому Функция y = sinx непрерывна в любой точке, поэтому 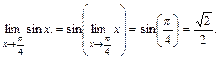 |
| пп 10. ФУНКЦИИ |
| п/п | Задание | Ответ |
| ПП 10. №1. | Укажите все номера целых чисел данного множества 1) 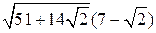 , 2) , 2) 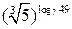 , 3) , 3) 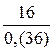 , 4) , 4) 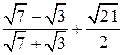 ,5) ,5) 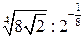 . РЕШЕНИЕ: 1) . РЕШЕНИЕ: 1) 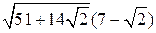 = = 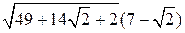 = = 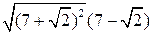 = = 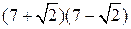 = =49-2=47 = =49-2=47 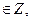 2) 2) 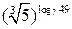 = = 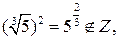 3) для перевода периодической десятичной дроби в рациональную сделаем следующее: обозначим периодическую дробь через x, умножим ее на 100 и вычтем из полученного равенства исходное, тем самым получим 3) для перевода периодической десятичной дроби в рациональную сделаем следующее: обозначим периодическую дробь через x, умножим ее на 100 и вычтем из полученного равенства исходное, тем самым получим 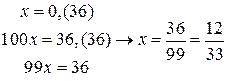 , , 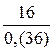 = = 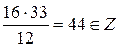 , 4) , 4) 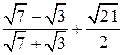 = = 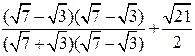 = = 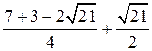 = = 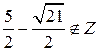 . 5) . 5) 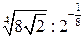 = = 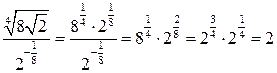 . . | 1), 3), 5) | |
| ПП 10. №2. | Найдите область определения и множество значений функции 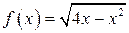 . ООФ находим из условия . ООФ находим из условия 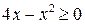 , , 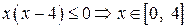 . ОЗФ находим из условий: . ОЗФ находим из условий: 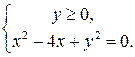 Допустимые значения параметра Допустимые значения параметра 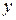 удовлетворяют неравенствам: удовлетворяют неравенствам: 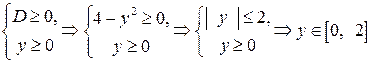 . . | 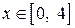 , , 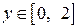 | |
| ПП 10. №3. | Изобразите график функции 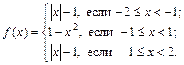 РЕШЕНИЕ: На полуинтервале [-1, 1) функция имеет вид смещенной параболы, ветви которой направлены вниз. Вне этого полуинтервала f(x) = | x | – 1, т.е. y = | x |опущенный на 1 вниз стандартный график РЕШЕНИЕ: На полуинтервале [-1, 1) функция имеет вид смещенной параболы, ветви которой направлены вниз. Вне этого полуинтервала f(x) = | x | – 1, т.е. y = | x |опущенный на 1 вниз стандартный график | 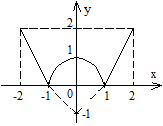 | |
| ПП 10. №4. | Изобразите график функции 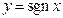 - знак - знак  , , 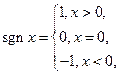 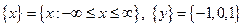 | 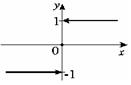 | |
| ПП 10. №5. | Функция Дирихле 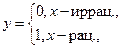 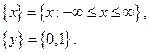 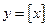 - целая часть - целая часть 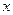 (наибольшее целое, не превосходящее (наибольшее целое, не превосходящее 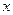 ) ) 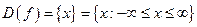 , , 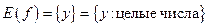 ; эта функция может быть задана в виде ; эта функция может быть задана в виде 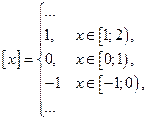 . . | 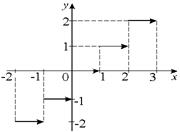 | |
| ПП 10. №6. | Найдите 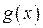 , если , если 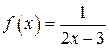 , , 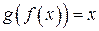 . Вычислите . Вычислите 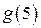 . . 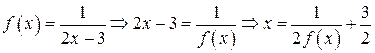 ; ; 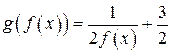 , значит, , значит, 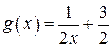 ; ; 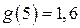 . . | 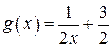 ; ; 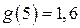 . . | |
| ПП 10. №7. | Вычислите односторонние пределы функции 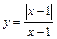 в точке x= 1. В точке x = 1 функция не определена, потому что знаменатель равен нулю. По определению модуля в точке x= 1. В точке x = 1 функция не определена, потому что знаменатель равен нулю. По определению модуля 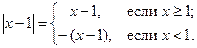 Левый предел: Левый предел: 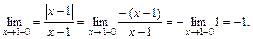 Правый предел: Правый предел: 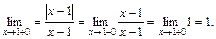 Односторонние пределы конечны, но не равны друг другу, функция имеет в точке x = 1 разрыв 1-го рода. Односторонние пределы конечны, но не равны друг другу, функция имеет в точке x = 1 разрыв 1-го рода. | 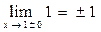 | |
| ПП 10. №8. | Установите, какого рода разрыв в точке х = 0 имеет функция 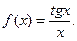 РЕШЕНИЕ: В теории пределов был доказан 1-й замечательный предел РЕШЕНИЕ: В теории пределов был доказан 1-й замечательный предел 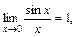 следствием которого является предел следствием которого является предел 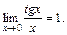 Стремление х®0 произвольно, поэтому Стремление х®0 произвольно, поэтому 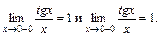 Тем самым доказано, что Тем самым доказано, что 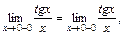 но в самой точке х0 = 0 функция не определена. Следовательно, выполняется определение точки устранимого разрыва. но в самой точке х0 = 0 функция не определена. Следовательно, выполняется определение точки устранимого разрыва. | точка устранимого разрыва | |
| ПП 10. №9. | Вычислите односторонние пределы 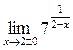 . РЕШЕНИЕ: . РЕШЕНИЕ: 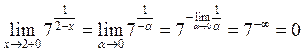 , , 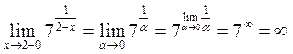 . Функция имеет в точке x = 1 разрыв 2-го рода. . Функция имеет в точке x = 1 разрыв 2-го рода. | 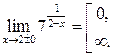 | |
| ПП 10. №10. | Докажите (найдите  ), что функция ), что функция  непрерывна в точке непрерывна в точке 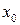 , если , если 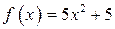 , , 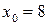 . РЕШЕНИЕ: По определению непрерывности требуется доказать, что . РЕШЕНИЕ: По определению непрерывности требуется доказать, что 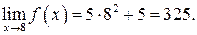 По определению предела требуется доказать, что По определению предела требуется доказать, что 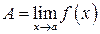  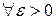 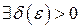 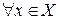 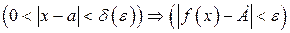 . 1). Возьмем произвольное . 1). Возьмем произвольное 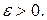 2). Так как 2). Так как 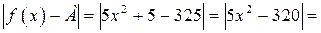 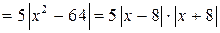 Положим Положим 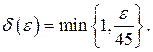 3). Возьмем 3). Возьмем 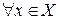 . Тогда если . Тогда если 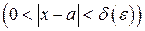 то то 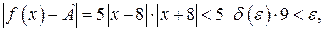 ч.т.д. ч.т.д. | ||
| ПП 10. №11. | Определите точки разрыва функции 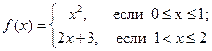 и исследовать характер разрыва. РЕШЕНИЕ: Функция имеет различный вид на отрезке [0, 1] и полуинтервале (1, 2], поэтому точка х = 1 может быть точкой разрыва. Левый предел: и исследовать характер разрыва. РЕШЕНИЕ: Функция имеет различный вид на отрезке [0, 1] и полуинтервале (1, 2], поэтому точка х = 1 может быть точкой разрыва. Левый предел: 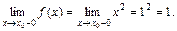 Правый предел: Правый предел: 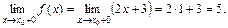 Односторонние пределы существуют и не равны друг другу. Следовательно, точка х = 1 является точкой разрыва 1-го рода. Односторонние пределы существуют и не равны друг другу. Следовательно, точка х = 1 является точкой разрыва 1-го рода. | разрыв 1-го рода |
| ПП 10. №12. | Определите точки разрыва функции 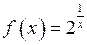 и исследуйте их характер. РЕШЕНИЕ: Функция не определена, следовательно, разрывна в точке х = 0. Вычислим левый предел, учитывая, что показательная функция y = ax, a > 1, стремится к нулю при х ® - ¥. Кроме того, функция y = 1/x является бесконечно большой, потому что х®0 и х < 0. Итак, и исследуйте их характер. РЕШЕНИЕ: Функция не определена, следовательно, разрывна в точке х = 0. Вычислим левый предел, учитывая, что показательная функция y = ax, a > 1, стремится к нулю при х ® - ¥. Кроме того, функция y = 1/x является бесконечно большой, потому что х®0 и х < 0. Итак, 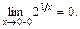 Вычислим правый предел, учитывая, что показательная функция y = ax, где a > 1, стремится к бесконечности при х ® +¥. Кроме того, функция является бесконечно большой, потому что х®0 и х > 0. Итак, Вычислим правый предел, учитывая, что показательная функция y = ax, где a > 1, стремится к бесконечности при х ® +¥. Кроме того, функция является бесконечно большой, потому что х®0 и х > 0. Итак, 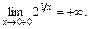 Поскольку правый предел бесконечен по определению, то точка х = 0 является точкой разрыва 2-го рода. Поскольку правый предел бесконечен по определению, то точка х = 0 является точкой разрыва 2-го рода. | х = 0 – точка разрыва 2-го рода. |
| ПП 10. №13. | Установите, какого рода разрыв в точке х = 0 имеет функция 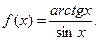 РЕШЕНИЕ: РЕШЕНИЕ: 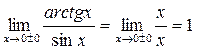 . . 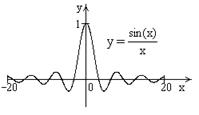 Односторонние пределы существуют и равны друг другу. Следовательно, точка х = 1 является точкой устранимого разрыва, устранить который можно доопределив функцию: Односторонние пределы существуют и равны друг другу. Следовательно, точка х = 1 является точкой устранимого разрыва, устранить который можно доопределив функцию: 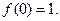 | устранимый разрыв |
| ПП 10. №14. | Имеет ли корень уравнение sinx – x + 1 = 0? РЕШЕНИЕ: Рассмотрим функцию f(x) = sinx – x + 1, которая непрерывна на всей числовой оси, поскольку является суммой непрерывных на числовой оси функций y = sinx и y = -x + 1. легко установить, что функция меняет знак, поскольку f(0) = 1, а f(2p) = -2p + 1 < 0. Следовательно, функция равняется нулю внутри отрезка [0, 2p], то есть имеется по крайней мере один корень исходного уравнения. | да |
| ПП 10. №15. | Исследуйте поведение функции 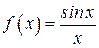 в точке в точке 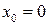 . РЕШЕНИЕ: В точке . РЕШЕНИЕ: В точке 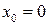 функция не определена, функция не определена, 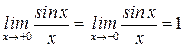  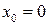 является точкой устранимого разрыва. является точкой устранимого разрыва.  Чтобы функция стала непрерывной в точке Чтобы функция стала непрерывной в точке 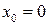 , положим , положим 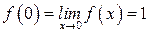 Новая, доопределенная функция Новая, доопределенная функция 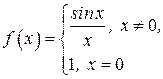 будет непрерывна на новой области определения – всей числовой оси. будет непрерывна на новой области определения – всей числовой оси. | |
| ПП 10. №16. | Принимает ли функция 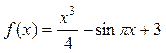 значение значение 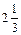 внутри отрезка [-2, 2]? РЕШЕНИЕ: Функция является непрерывной на [-2, 2]. Кроме того, на концах отрезка функция принимает числовые значения f (-2)=1, f (2) = 5. Так как внутри отрезка [-2, 2]? РЕШЕНИЕ: Функция является непрерывной на [-2, 2]. Кроме того, на концах отрезка функция принимает числовые значения f (-2)=1, f (2) = 5. Так как 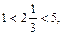 то найдется точка c Î (-2, 2) такая, что то найдется точка c Î (-2, 2) такая, что 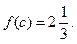 | да |
| ПП 10. №17. | Найдите функцию, обратную функции 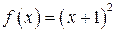 при при 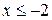 . РЕШЕНИЕ: . РЕШЕНИЕ: 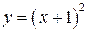 , , 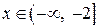 , , 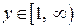 . При . При 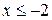 функция функция 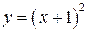 монотонно убывает, значит, существует обратная. Выразим монотонно убывает, значит, существует обратная. Выразим 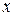 через через 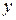 , учитывая, что , учитывая, что 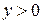 . Получим: . Получим: 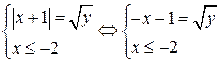 , , 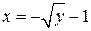 . Поменяем местами . Поменяем местами 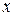 и и 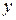 . . 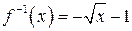 , , 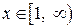 , , 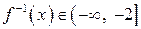 . . 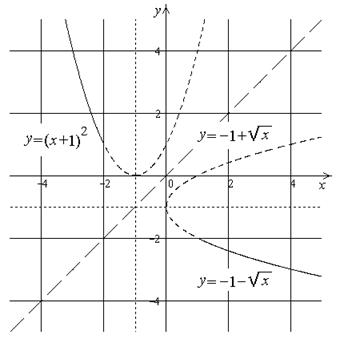 Область определения и область значений исходной и обратной функции меняются местами. Графики функций симметричны относительно прямой Область определения и область значений исходной и обратной функции меняются местами. Графики функций симметричны относительно прямой 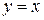 . . | 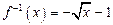 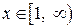 |
