Напряжение в поперечных сечениях стержня
Нормальная сила 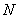 приложена в центре тяжести сечения, является равнодействующей внутренних сил в сечении и, в соответствии с этим, определяется следующим образом:
приложена в центре тяжести сечения, является равнодействующей внутренних сил в сечении и, в соответствии с этим, определяется следующим образом:
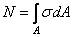 .
.
Но из этой формулы нельзя найти закон распределения нормальных 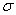 напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.
напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.
Если на боковую поверхность этого стержня нанести прямоугольную сетку (рис. 2.2, б), то после нагружения поперечные линии а-а, b-b и т.д. переместятся параллельно самим себе, откуда следует, что все поверхностные продольные волокна удлинятся одинаково. Если предположить также, что и внутренние волокна работают таким же образом, то можно сделать вывод о том, что поперечные сечения в центрально растянутом стержне смещаются параллельно начальным положениям, что соответствует гипотезе плоских сечений (гипотезе Бернулли).
Значит, все продольные волокна стержня находятся в одинаковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть также одинаковы и равны
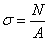 , (2.2)
, (2.2)
где A - площадь поперечного сечения стержня.
В сечениях, близких к месту приложения внешних сил, гипотеза Бернулли нарушается: сечения искривляются, и напряжения в них распределяются неравномерно. По мере удаления от сечений, в которых приложены силы, напряжения выравниваются, и в сечениях, удаленных от места приложения сил на расстояние, равное наибольшему из размеров поперечного сечения, напряжения можно считать распределенными по сечению равномерно. Это положение, называемое принципом Сен-Венана, позволяет при определении напряжений в сечениях, достаточно удаленных от мест приложения внешних сил, не учитывать способ их приложения, заменять систему внешних сил статически эквивалентной системой. Например, экспериментально установлено, что во всех трех случаях нагружения стержня (рис. 2.7, а) значения напряжений в сечениях, удаленных от крайних сечений на расстояние не менее высоты сечения 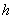 , одинаковы:
, одинаковы: 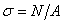 (рис. 2.7, б), а в сечениях, близких к местам приложения внешних сил, распределения напряжений по сечению существенно различны (рис. 2.7, в).
(рис. 2.7, б), а в сечениях, близких к местам приложения внешних сил, распределения напряжений по сечению существенно различны (рис. 2.7, в).
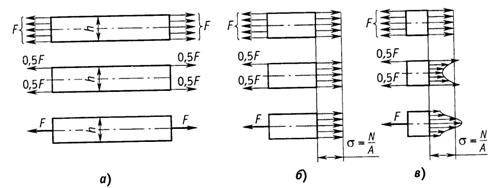
Рис.2.7
Высказанное предположение о равномерном распределении нормальных напряжений в поперечном сечении справедливо для участков, достаточно удаленных от мест: резкого изменения площади поперечного сечения (рис. 2.2, в); скачкообразного изменения внешних нагрузок; скачкообразного изменения физико-механических характеристик конструкций.
Нормальные напряжения при сжатии определяют также, как и при растяжении, но считают отрицательными.
Следует помнить, что длинные (тонкие) стержни, нагруженные сжимающими силами, могут потерять устойчивость. Расчет стержней на устойчивость рассмотрен в разделе «Устойчивость».
В инженерных сооружениях встречаются растянутые или сжатые элементы, имеющие отверстия. В сечениях с отверстием определяют осредненные нормальные напряжения по формуле
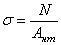 , (2.3)
, (2.3)
где 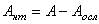 - площадь поперечного сечения нетто;
- площадь поперечного сечения нетто; 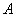 - площадь поперечного сечения брутто;
- площадь поперечного сечения брутто; 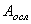 - площадь его ослабления.
- площадь его ослабления.
