Тема 3, 4. Диференціювання неявних та параметрично заданих функцій

Похідна неявної функції.

Нехай рівняння F (x; y) = 0 визначає у як неявну функцію від х. Надалі будемо вважати, що ця функція — диференційована.

Потрібно продиференціювати за змінною х обидві частини рівняння F (x; y) = 0, дістанемо рівняння першого степеня відносно 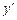. З цього рівняння легко знайти 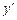, тобто похідну неявної функції.

Приклад 1. Знайти 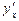з рівняння .

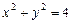l Оскільки у є функцією від х, то у² розглядатимемо як складну функцію від х, тобто .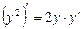

Диференціюємо по х обидві частини заданого рівняння, дістанемо 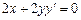. Звідси .

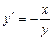Приклад 2.

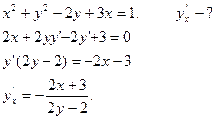
Диференціювання функцій, заданих у параметричній формі.

Нехай функція y від x задана у параметричній формі, тобто

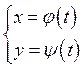
Похідну 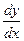можна знайти, не знаючи явної залежності y від x.

Достатньо врахувати, що

1) Похідна 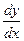є частка від ділення двох диференціалів;

2) Форма диференціалів 1-го порядку не залежить від вибору аргументу.

Одержимо ; .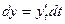

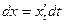Відношення цих величин дає : =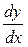

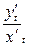
Для похідної 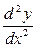запишемо =

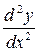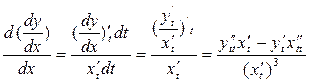
Приклад.

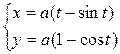
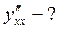
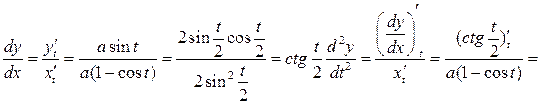
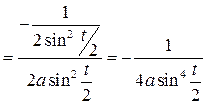
Тема 5. Геометричний та фізичний зміст похідної

Геометричний зміст похідної

Дамо загальне означення дотичної. Розглянемо криву L і на ній точки M та M₁ .

Пряму 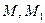, що проходить через ці точки називають січною. Нехай точка 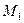, рухаючись вздовж кривої, наближається до точки М. Тоді січна повертатиметься навколо точки М, а довжина відрізка 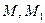прямуватиме до нуля.

Якщо при цьому і величина кута 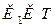прямує до нуля, то пряму МТ називають граничним положенням січної 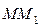, тобто дотичної до кривої в точці М.

З означення випливає, що існування дотичної не залежить, з якого боку точка 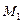наближається до точки М.

Якщо січна 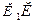наближається до різних прямих, або взагалі не наближається ні до якої прямої, то М – точка ізлому і вважається, що в точці М дотичної немає.

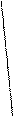
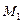
М

Нехай крива задана рівнянням y=f(x) і має в точці М(х,у) не вертикальну дотичну. Розглянемо задачу про знаходження кутового коефіцієнта цієї дотичної.

Y

y+Δy

Δy

y M A

y=f(x)

α

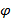
T 0 x

x Δx x+Δx

Надамо аргументу х приросту Δх: тоді значенню (х+Δх) відповідатимуть значення функції y+Δy = f(x+Δx) і точка 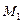(х+Δх; y+Δx) на кривій.

Проведемо січну 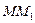і позначимо через φ кут, утворений цією січною з додатним напрямом осі Ох. Кутовий коефіцієнт січної дорівнює

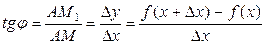
Якщо 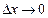, то точка 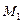прямує до точки М вздовж кривої, а січна 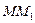, повертаючись навколо точки М, переходить у дотичну МТ. Кут φ при цьому прямує до деякого граничного значення α.

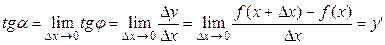
Похідна 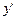, знайдена від функції y=f(x) та обчислена у точці 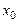, тобто 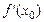є кутовий коефіцієнт дотичної до графіка функції y=f(x) у точці з абсцисою 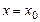. Це геометричний зміст похідної.

Рівняння дотичної, яка проходить через точки 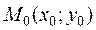буде:

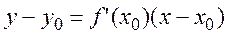
Фізичний зміст похідної

Нехай s = s (t) – закон прямолінійного руху. Тоді 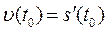висловлює миттєву швидкість руху в момент часу t_0. Друга похідна 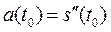висловлює миттєве прискорення в момент часу t _0.

Взагалі похідна функції y = f (x) в точці x ₀ висловлює швидкість зміни функції в точці x₀ . Тобто швидкість протікання процесу, описаного залежністю y = f (x).

Тема 6. Асимптоти.