Активные и реактивные составляющие токов и напряжений
При расчете электрических цепей переменного тока реальные элементы цепи (приемники, источники) заменяются эквивалентными схемами замещения, состоящими из комбинации идеальных схемных элементов R, L и С.
Пусть некоторый приемник энергии носит в целом активно-индуктивный характер (например, электродвигатель). Такой приемник может быть представлен двумя простейшими схемами замещения, состоящими из 2-х схемных элементов R и L: а) последовательной (рис. 51а) и б) параллельной (рис. 51б):
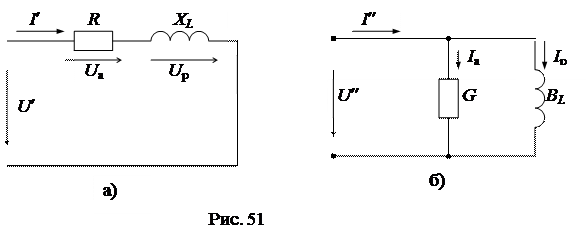 |
Обе схемы будут эквивалентны друг другу при условии равенства параметров режима на входе: 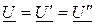 ,
, 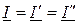 .
.
Для последовательной схемы (рис. 51а) справедливы соотношения:
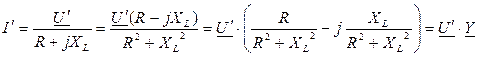 ,
,
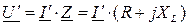 .
.
Для параллельной схемы (рис. 51б) справедливы соотношения:
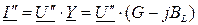 ,
,
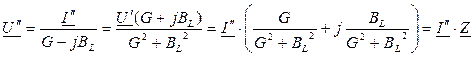 .
.
Сравнивая правые части уравнений для U и I, получим соотношения между параметрами эквивалентных схем:
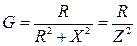 ,
, 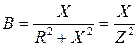 ,
, 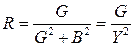 ,
, 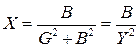 .
.
Из анализа полученных уравнений следует сделать вывод, что в общем случае 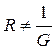 и
и 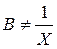 и соответственно
и соответственно 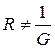 и
и 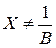 , как это имеет место для цепей постоянного тока.
, как это имеет место для цепей постоянного тока.
Математически любой вектор можно представить состоящим из суммы нескольких векторов или составляющих.
Последовательной схеме замещения соответствует представление вектора напряжения в виде суммы двух составляющих: активной составляющей Uа, совпадающей с вектором тока I, и реактивной составляющей Uр, перпендикулярной к вектору тока (рис. 52а):
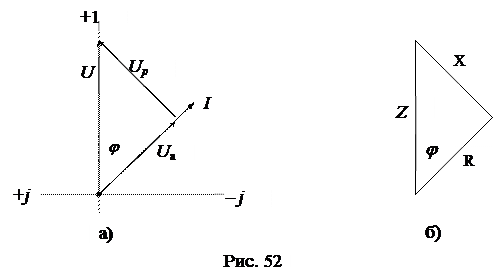 |
Из геометрии рис. 52а следуют соотношения: 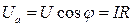 ,
, 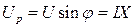 ,
, 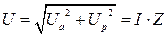 . Треугольник, составленный из векторов
. Треугольник, составленный из векторов 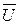 ,
, 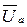 ,
, 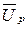 получил название треугольника напряжений.
получил название треугольника напряжений.
Если стороны треугольника напряжений разделить на ток I, то получится новый треугольник, подобный исходному, но сторонами которого являются полное сопротивление Z, активное сопротивление R и реактивное сопротивление X. Треугольник со сторонами Z, R, X называется треугольником сопротивлений (рис. 52б). Из треугольника сопротивлений следуют соотношения: R=Z×cosφ, X=Z×sinφ, 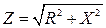 ,
, 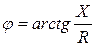 .
.
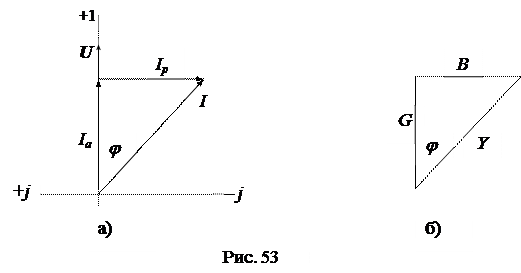
Параллельной схеме замещения соответствует представление вектора тока в виде суммы двух составляющих: активной составляющей Iа, совпадающей с вектором напряжения U, и реактивной составляющей Iр, перпендикулярной к вектору U (рис. 53а):
 |
Из геометрии рисунка следуют соотношения:
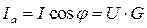 ,
, 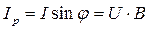 ,
, 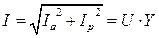 .
.
Треугольник, составленный из векторов 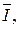
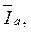
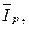 получил название треугольника токов.
получил название треугольника токов.
Если стороны треугольника токов разделить на напряжение U, то получится новый треугольник, подобный исходному, но сторонами которого являются проводимости: полная – Y, активная - G, реактивная – B (рис. 53б). Треугольник со сторонами Y, G, B называется треугольником проводимостей. Из треугольника проводимостей следуют соотношения:
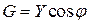 ,
, 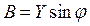 ,
, 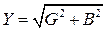 ,
, 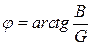 .
.
Разложение напряжений и токов на активные и реактивные составляющие является математическим приемом и применяется на практике для расчета несложных цепей переменного тока.
10. Передача энергии от активного двухполюсника (источника) к пассивному двухполюснику (приемнику)
Двухполюсником называется устройство или часть схемы (цепи) с двумя выводами (полюсами). Если внутри двухполюсника содержатся источники энергии, то он называется активным (A), в противном случае – пассивным (П).
Энергетические характеристики передачи энергии от активного двухполюсника (источника) к пассивному двухполюснику (приемнику) на переменном токе зависят от соотношения параметров приемника и источника между собой (рис. 54)
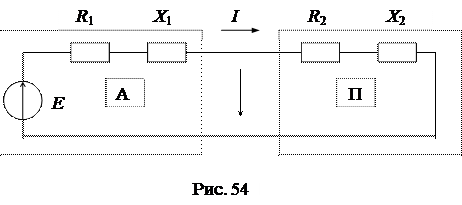 |
По закону Ома ток в схеме равен:
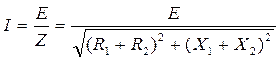 .
.
Активная мощность приемника:
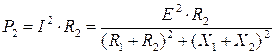 .
.
Активная мощность источника: PE=E×I.
При постоянных параметрах источника энергии активная мощность приемника зависит от его параметров: 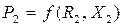 . Исследуем эту функцию на максимум при изменении отдельных параметров.
. Исследуем эту функцию на максимум при изменении отдельных параметров.
Условие первое: X2 = var, R2=const:
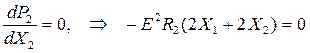 или
или 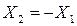 .
.
Максимум мощности приемника 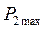 имеет место при условии равенства реактивных сопротивлений приемника и источника по модулю и противоположности их по знаку, например, если реактивное сопротивление источника носит индуктивный характер, то реактивное сопротивление приемника должно быть емкостным, и наоборот.
имеет место при условии равенства реактивных сопротивлений приемника и источника по модулю и противоположности их по знаку, например, если реактивное сопротивление источника носит индуктивный характер, то реактивное сопротивление приемника должно быть емкостным, и наоборот.
Условие второе: R2 = var, X2 = const.
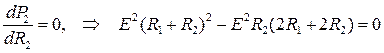 или
или 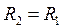 .
.
Максимум мощности приемника имеет место при равенстве активных сопротивлений приемника и источника.
Абсолютный максимум мощности приемника наблюдается при выполнении обоих условий и равен:
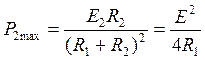 .
.
В режиме максимума потребляемой мощности работают приемники в линиях связи.
Коэффициент полезного действия передачи энергии от источника к приемнику равен отношению активных мощностей 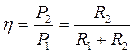 и не зависит от величины их реактивных сопротивлений.
и не зависит от величины их реактивных сопротивлений.
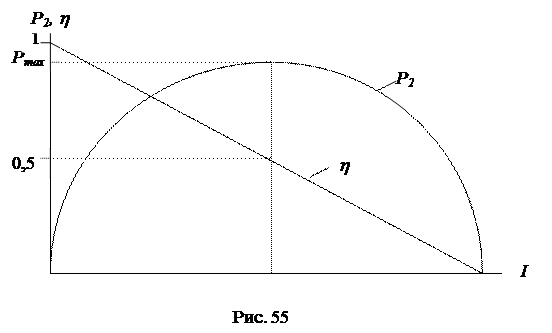
В режиме абсолютного максимума мощности приемника КПД составляет только 0,5. Линии электропередачи (ЛЭП) работают с КПД h = 0,90÷0,95, что соответствует соотношению активных сопротивлений приемника и источника (генератора + ЛЭП) R2/R1=10÷20.
На графической диаграмме рис. 2 показаны энергетические характеристики передачи энергии при R2= var, Х2=const в функции тока: P2, h = f(I).
 |
