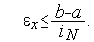Некоторые свойства алгоритм Фибоначчи

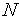Утверждение 1. Для любого [1, -2] алгоритм Фибоначчи обладает следующим свойством: одна из точек 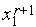, 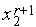совпадает с одной из точек 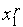, 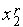(см. рис. 1).

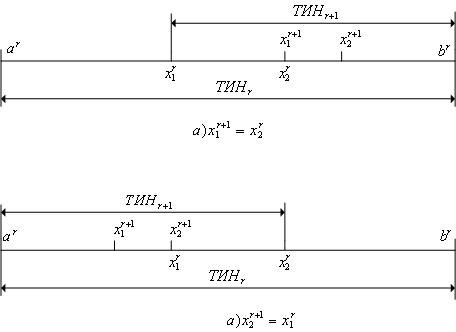Рис. 1. К утверждению 1.

Доказательство. Пусть на 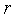-й итерации 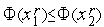-ситуация б на рис. 1. В соответствии с алгоритмом Фибоначчи 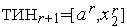причем, очевидно, ТИН_r+1. Рассмотрим точку

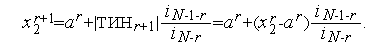
Подставим сюда значение координаты точки

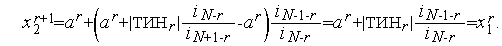
Аналогично проводится доказательство для случая 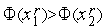- ситуация а на рис. 1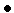

Указанное свойство алгоритма Фибоначчи позволяет на каждой итерации (кроме первой) производить испытания только в одной точке.

Утверждение 2. Точки 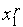, 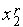расположены симметрично относительно концов текущего интервала неопределенности , т.е. расстояние точки 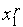до точки 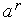равно расстоянию точки 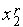до точки 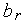или, что то же самое, .

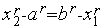Доказательство. В соответствии с алгоритмом Фибоначчи имеем:

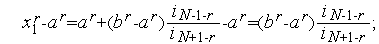
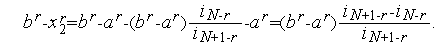
Но из формулы (1) следует, что 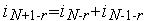. Подставляя это в предыдущую формулу, получим

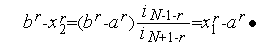
Утверждение 3. В результате любой итерации 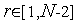алгоритма Фибоначчи длина текущего интервала неопределенности уменьшается в 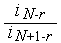раз.

Доказательство. Поскольку 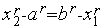(см. утверждения 2), достаточно рассмотреть только один из интервалов , 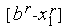. Рассмотрим первый из указанных интервалов:

= +( - ) - =( - )

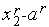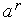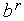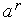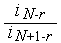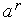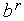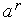Утверждение 4. При достаточно больших 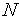в результате одной итерации алгоритма Фибоначчи длина текущего интервала неопределенности уменьшается примерно в 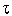раз.

Доказательство. Справедливость утверждения следует из утверждения 3 и из того факта, что при достаточно больших 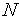имеем (см. (2)):

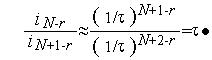
Из утверждения 4 следует, что при достаточно больших N алгоритм Фибоначчи практически идентичен алгоритму золотого сечения (см. следующий параграф).

Утверждение 5. В результате 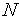итераций алгоритма Фибоначчи длина текущего интервала неопределенности становится равной

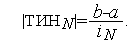(3)

Доказательство. Из утверждения 3 следует, что:

· после первой итерации длина ТИН равна ;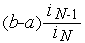

· после второй итерации - ;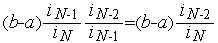

· после итерации номер 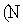-2) длина ТИН равна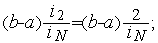

· после итерации номер 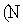-1) длина ТИН не меняется;

· после итерации номер 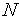длина ТИН уменьшается в два раза и становится равной

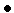
Поэтому количество итераций 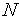, необходимых для нахождения минимума функции с точностью 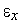, находится из условия