Ньютонның модификацияланған әдісі
Лекция № 1-3 Бір белгісізді теңдеулерді шешу.
Жанамалар әдісі
Біріккен әдіс
Итерациялық әдіс.
3.1 Ньютон әдісі (жанамалар әдісі)
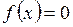 теңдеудің
теңдеудің 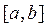 аралықта ажыратылған түбірі
аралықта ажыратылған түбірі 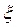 болсын. Біз түбірдің
болсын. Біз түбірдің 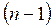 -ші жуықтауында
-ші жуықтауында 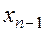 түбірді таптық делік. Онда
түбірді таптық делік. Онда 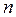 -ші жуықтау
-ші жуықтау 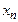 -ді төмендегіше бағалаймыз.
-ді төмендегіше бағалаймыз.
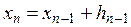 . (3.15)
. (3.15)
деп аламыз.
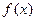 - ты
- ты 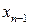 нүктеде қатарға жіктеп аламыз:
нүктеде қатарға жіктеп аламыз:
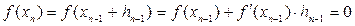 .
.
Бұл жерден
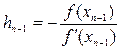 . (3.16)
. (3.16)
(3.16)-ны (3.15) формулаға қойып аламыз:
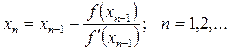 (3.17)
(3.17)
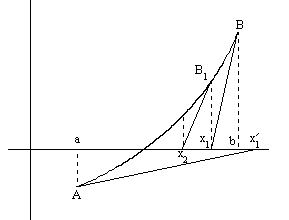
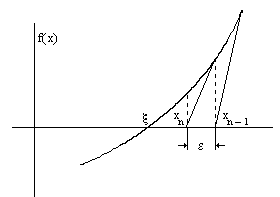
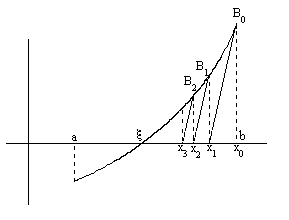
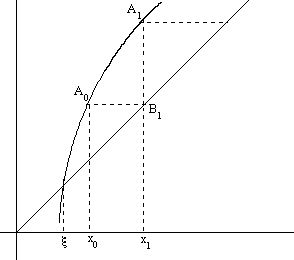
Сурет 1.
Ньютон әдісінің геометриялық мағынасы:
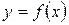 қисықтың доғасы, сол қисықтың әйтеуір бір нүктесіне жүргізілген жанамаға эквивалент. (Сурет 1-ді қараңыз.)
қисықтың доғасы, сол қисықтың әйтеуір бір нүктесіне жүргізілген жанамаға эквивалент. (Сурет 1-ді қараңыз.)
 нүктеде
нүктеде 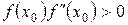 болады. Бұл жерде
болады. Бұл жерде 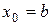 .
.
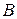 нүктеге жанама жүргіземіз, жанаманың
нүктеге жанама жүргіземіз, жанаманың  осімен қиылысуындағы нүкте
осімен қиылысуындағы нүкте 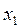 . Одан әрі
. Одан әрі 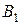 нүктеге жанама жүргізіп
нүктеге жанама жүргізіп 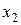 нүктені аламыз. т.с.с.
нүктені аламыз. т.с.с.
Егер 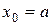 десек, онда
десек, онда 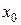 нүктеде
нүктеде 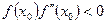 болады. Онда
болады. Онда  нүктедегі жанама
нүктедегі жанама  осін
осін 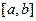 кесіндінің сыртында жатқан
кесіндінің сыртында жатқан 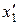 кесіп өтеді де алғашқы нүктені бұлай таңдауда Ньютон әдісі жинақталмайды. Ньютон әдісінің жинақты болуының жеткілікті шарты төмендегі теорема арқылы анықталады.
кесіп өтеді де алғашқы нүктені бұлай таңдауда Ньютон әдісі жинақталмайды. Ньютон әдісінің жинақты болуының жеткілікті шарты төмендегі теорема арқылы анықталады.
Теорема 5. Егер 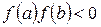 , болып,
, болып, 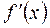 және
және 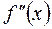 нольден өзгеше және
нольден өзгеше және 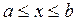 да белгілі бір таңбаны сақтаса, онда
да белгілі бір таңбаны сақтаса, онда
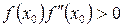 (3.18)
(3.18)
шартты қанағаттандырған бастапқы 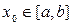 жуықтаудан бастап, (3.17) Ньютон әдісімен
жуықтаудан бастап, (3.17) Ньютон әдісімен 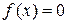 теңдеуінің бір ғана
теңдеуінің бір ғана 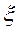 түбірін кез келген дәлдік дәрежесінде есептеп таба аламыз.
түбірін кез келген дәлдік дәрежесінде есептеп таба аламыз.
Дәлелдеуі:
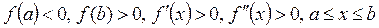
болсын. (3.18) теңсіздікке байланысты 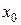 жатқан аралық ретінде,
жатқан аралық ретінде, 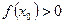 болатын кесіндіні аламыз, қазіргі жағдайда b нүктесі.
болатын кесіндіні аламыз, қазіргі жағдайда b нүктесі.
Демек, 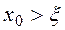 . Енді барлық жуықтаулар
. Енді барлық жуықтаулар 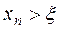 , сонымен қатар барлық
, сонымен қатар барлық 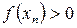 екендігін дәлелдейік.
екендігін дәлелдейік. 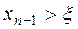 болсын.
болсын.
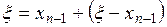 деп алайық.
деп алайық.
Тейлор формуласын қолдансақ:
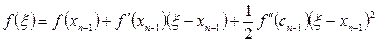 ,
,
бұл жерде
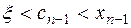 .
. 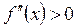 , болғандықтан
, болғандықтан
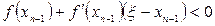
және, осылайша
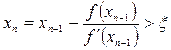 дәлелдеу керегі сол. (3.19)
дәлелдеу керегі сол. (3.19)
(3.19)-дан 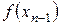 және
және 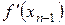 -дің таңбаларын ескеріп
-дің таңбаларын ескеріп 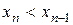 аламыз, яғни шекараланған монотон кемімелі тізбек аламыз
аламыз, яғни шекараланған монотон кемімелі тізбек аламыз
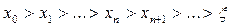 .
.
Демек, 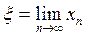 бар..
бар..
(3.17)-де шекке өтіп, 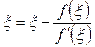 аламыз, яғни
аламыз, яғни 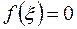 , демек бұл жерден,
, демек бұл жерден, 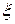 - түбір д.к.с.
- түбір д.к.с.
Ньютон әдісінің жинақталу жылдамдығын бағалайық. (3.17)-ден
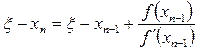 . (3.20)
. (3.20)
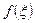 -ді төмендегіше жазайық.
-ді төмендегіше жазайық.
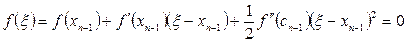 ,
,
бұл жерден
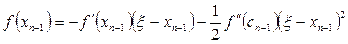 . 3.21)
. 3.21)
(3.21)-ді (3.20)-ға қойып табамыз,
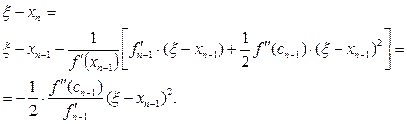
Бұл жерден
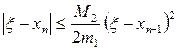 (3.22)
(3.22)
Бұл жерде 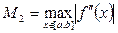 ,
, 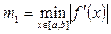
 |
Сонымен Ньютон әдісінің жинақталу жылдамдығы квадратты.
Сурет 2.
Итерациялық процестің аяқталу критерийі төмендегіше:
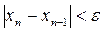 .
.
Ескерту. Жалпы жағдайда 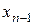 және
және 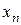 екі тізбектің
екі тізбектің 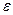 дәлдікте жинақталуы
дәлдікте жинақталуы 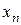 және
және 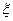 -дің сәйкес келуіне (сурет 2) кепілдік бермейді. Сондықтан да
-дің сәйкес келуіне (сурет 2) кепілдік бермейді. Сондықтан да 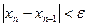 айырымнан басқа f (xn):
айырымнан басқа f (xn): 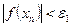 функция мәндерін де тексеруге болады.
функция мәндерін де тексеруге болады.
Ньютонның модификацияланған әдісі
Ньютон әдісін модификациялау үшін 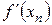 туындыны
туындыны
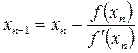
формуладағы 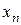 нүктеде
нүктеде 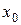 нүктедегі
нүктедегі 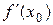 туындымен алмастырамыз, яғни
туындымен алмастырамыз, яғни 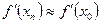 деп аламыз. Нәтижеде
деп аламыз. Нәтижеде
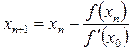 (
( 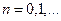 ).(3.23)
).(3.23)
Бұл тәсілдің геометриялық мағынасы: 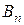 нүктедегі жанамаларды
нүктедегі жанамаларды 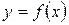 қисығына
қисығына 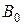 нүктеде жүргізілген жанамаларға параллель түзулермен алмастырамыз. (сурет 3).
нүктеде жүргізілген жанамаларға параллель түзулермен алмастырамыз. (сурет 3).
Сурет.3. Модификацияланған Ньютон әдісі.
Бұл жерде қайта-қайта 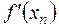 туындыны есептей берудің қажеті жоқ. (3.23) процесінің жинақталуын төмендегі теорема қамтамасыз етеді.
туындыны есептей берудің қажеті жоқ. (3.23) процесінің жинақталуын төмендегі теорема қамтамасыз етеді.
Теорема 6. 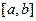 -да екі рет дифференциялданушы
-да екі рет дифференциялданушы 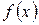 функция берілсін, сонымен қатар төмендегі шарттар орындалсын.
функция берілсін, сонымен қатар төмендегі шарттар орындалсын.
а) 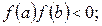
б) 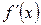 және
және 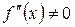 және
және 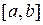 -да таңбаларын сақтасын.
-да таңбаларын сақтасын.
Онда
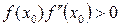
шартты қанағаттандырушы 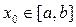 алғашқы жуықтаудан Ньютонның модификацияланған әдісімен кез келген дәлдіктегі бір ғана
алғашқы жуықтаудан Ньютонның модификацияланған әдісімен кез келген дәлдіктегі бір ғана 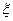 түбірді есептеп таба аламыз.
түбірді есептеп таба аламыз.
Дәлелдеуі. 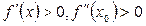 (сурет.3) болсын. Онда
(сурет.3) болсын. Онда 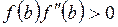 болғандықтан
болғандықтан 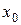 ретінде
ретінде 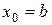 нүктені аламыз. (3.23)-тен
нүктені аламыз. (3.23)-тен 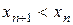 екендігі келіп шығады, яғни
екендігі келіп шығады, яғни 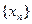 тізбек кемімелі болады.
тізбек кемімелі болады.
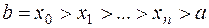 . (3.24)
. (3.24)
Енді осы тізбектің шегі 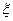 екендігін көрсетеміз.
екендігін көрсетеміз. 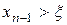 болсын.
болсын. 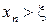 екендігін дәлелдейміз. Ол үшін Ньютон формуласында алынған
екендігін дәлелдейміз. Ол үшін Ньютон формуласында алынған 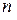 -ші жуықтауды(формула (3.17) жазамыз және Ньютонның модификацияланған әдісі (3.23) бойынша
-ші жуықтауды(формула (3.17) жазамыз және Ньютонның модификацияланған әдісі (3.23) бойынша
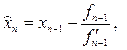
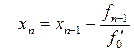
және айырымды табамыз.
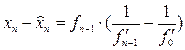 . (3.25)
. (3.25)
Дөңес функциялар теориясынан, егер 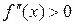 және
және 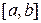 -да таңбасын сақтаса, онда
-да таңбасын сақтаса, онда  дөңес болады. Дөңес
дөңес болады. Дөңес  функциялар үшін
функциялар үшін 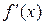 туындылар кемімелі емес, яғни
туындылар кемімелі емес, яғни 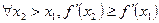 . Сондықтан
. Сондықтан
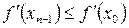 .
.  (3.26)
(3.26)
(3.26)-ны ескере отырып (11)-ден 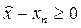 .
.
5-теоремадан Ньютон әдісінің жинақтылығын 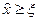 алдық, сондықтан
алдық, сондықтан 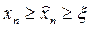 . Бұл жерден
. Бұл жерден
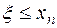 . (3.27)
. (3.27)
Сонымен, (3.24) және (3.27)-ден кемімелі тізбекке ие боламыз.
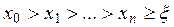 .
.
Сонымен кез келген кішкентай оң 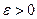 үшін,
үшін, 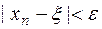 . Болатын
. Болатын 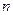 -ді көрсетуге болады. Теорема дәлелденді.
-ді көрсетуге болады. Теорема дәлелденді.
Біріккен тәсіл
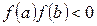 болсын, ал
болсын, ал 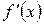 және
және 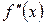
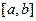 -да таңбаларын сақтасын. Хордалар және Ньютон әдістерін біріктіріп, түбірді іздеуді және итерациялық процестің жинақталуын тездетуге болады. Нәтижеде әрбір қадамда түбір жатқан интервалдың екі шетінің де мәндерін табатын біріккен тәсілге ие боламыз. Хордалар тәсіліндегідей келесі жағдайларды қарастырамыз.
-да таңбаларын сақтасын. Хордалар және Ньютон әдістерін біріктіріп, түбірді іздеуді және итерациялық процестің жинақталуын тездетуге болады. Нәтижеде әрбір қадамда түбір жатқан интервалдың екі шетінің де мәндерін табатын біріккен тәсілге ие боламыз. Хордалар тәсіліндегідей келесі жағдайларды қарастырамыз.
1. Егер 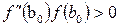 (яғни
(яғни 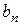 - қимылдамайтын, сурет 4) онда
- қимылдамайтын, сурет 4) онда
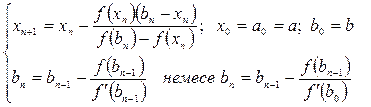 (3.28)
(3.28)
Бұл жерде 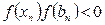
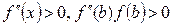
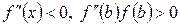
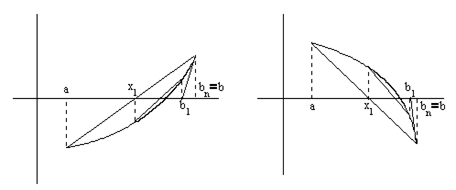 |
сурет. 4а сурет. 4б
2. Егер 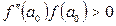 (
( 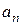 - қимылдамаса (сурет 5), онда
- қимылдамаса (сурет 5), онда
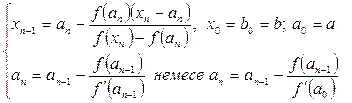 (3.29)
(3.29)
Бұл жерде 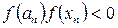 .
.
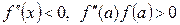
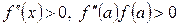
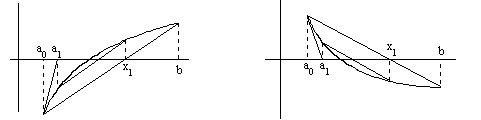 |
сурет. 5а сурет. 5б
Итерация әдісі
Теңдеуді сандық шешудің тиімді әдістерінің бірі итерация әдісі болып табылады.
Теңдеу берілсін.  .
.
Оны тең күшті  . (3.30) теңдеуімен алмастырамыз.
. (3.30) теңдеуімен алмастырамыз.
Алғашқы жуық түбір  -ді таңдап аламыз да оны (3.31) теңдеудің оң жағына апарып қоямыз. Сонда әйтеуір бір
-ді таңдап аламыз да оны (3.31) теңдеудің оң жағына апарып қоямыз. Сонда әйтеуір бір 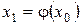 . (3.32)
. (3.32)
санға ие боламыз. (3.32)-нің оң жағына 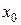 -дің орнына
-дің орнына 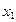 санын қойып
санын қойып
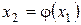 .
.
санға ие боламыз. Осы процесті қайталап,
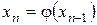 (
( 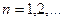 ). (3.33) сандар тізбегіне ие боламыз.
). (3.33) сандар тізбегіне ие боламыз.
Егер осы тізбек жинақты болса, яғни 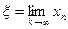 шек бар болса, онда (3.33) теңдеуде шекке көшіп және
шек бар болса, онда (3.33) теңдеуде шекке көшіп және 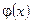 функцияны үздіксіз деп,
функцияны үздіксіз деп,
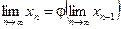 немесе
немесе 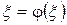 -ті табамыз.
-ті табамыз.
 |
Сонымен,
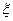 шек (3.33) теңдеудің шегі болады және оны (3.33) формуламен кез келген дәлдікте есептеуге болады.
шек (3.33) теңдеудің шегі болады және оны (3.33) формуламен кез келген дәлдікте есептеуге болады. сурет. 8а сурет. 8б
 |
сурет. 9.
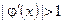 - жинақталмайтын процесс
- жинақталмайтын процесс
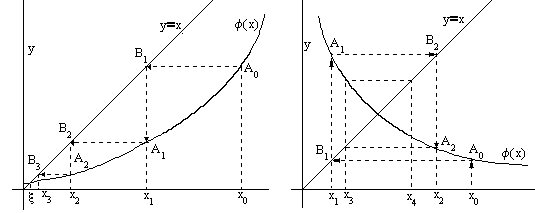
8а, 8б суреттерде 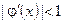 түбірдің маңайында итерациялық процесс жинақты. Бірақ, егер
түбірдің маңайында итерациялық процесс жинақты. Бірақ, егер 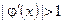 жағдайды қарастырсақ, онда итерациялық процесс жинақсыз болуы мүмкін (сурет 9).
жағдайды қарастырсақ, онда итерациялық процесс жинақсыз болуы мүмкін (сурет 9).
Итерациялық процесстің жинақты болуының жеткілікті шарты.
Теорема 7. 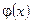 функция
функция 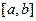 -да анықталған және дифференциялданушы болсын, сонымен қатар барлық
-да анықталған және дифференциялданушы болсын, сонымен қатар барлық 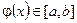 және
және 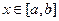 -да
-да 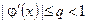 болсын. Онда
болсын. Онда 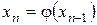 итерациялық процесс алғашқы
итерациялық процесс алғашқы 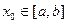 мәнге байланыссыз жинақты және
мәнге байланыссыз жинақты және 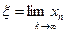 шектің мәні
шектің мәні 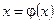 теңдеудің
теңдеудің 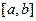 кесіндідегі жалғыз мәні болады.
кесіндідегі жалғыз мәні болады.
Дәлелдеуі: Екі тізбектелген жуықтауларды қарастырайық 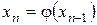 және
және 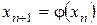 және олардың айырымын қарайық
және олардың айырымын қарайық 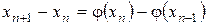 . Лагранж теоремасы бойынша оң жағы былай болуы мүмкін.
. Лагранж теоремасы бойынша оң жағы былай болуы мүмкін.
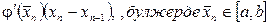 .
.
Онда
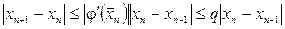 .
.
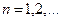 деп,
деп, 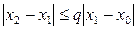
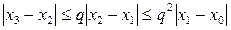
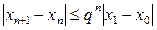 (3.34)
(3.34)
(3.34) тен 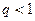 шарт бойынша
шарт бойынша 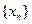 тізбек әйтеуір бір
тізбек әйтеуір бір 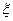 санға жинақталады, яғни
санға жинақталады, яғни 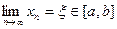 , демек
, демек 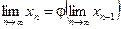 (
( 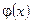 -функцияның үздіксіздігінен) немесе
-функцияның үздіксіздігінен) немесе
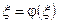 теорема дәлелденді.
теорема дәлелденді.
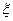 түбірдің қателігі үшін келесі формуланы алуға болады.
түбірдің қателігі үшін келесі формуланы алуға болады.
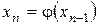 .
.
Ары қарай 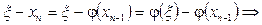
Енді 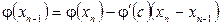
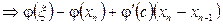 .
.
Нәтижеде 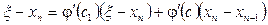
немесе
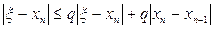
Бұл жерден 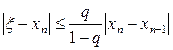 , (3.35)
, (3.35)
бұдан 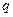 1-ге жақын болғанда
1-ге жақын болғанда 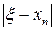 шама
шама 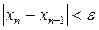 болғанына қарамай өте үлкен болуы мүмкін, бұл жерде
болғанына қарамай өте үлкен болуы мүмкін, бұл жерде 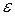 -берілген сан.
-берілген сан. 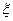 -ді
-ді 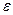 дәлдікпен есептеу үшін,
дәлдікпен есептеу үшін,
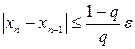 . (3.36)
. (3.36)
болуын қамтамасыз ету керек.
Онда (3.36)-ны (3.35)-ке қойып, 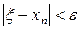 -ді аламыз.
-ді аламыз.
Егер 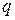 өте аз болса, онда (3.35)-дың орнына
өте аз болса, онда (3.35)-дың орнына
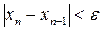
ды алуға болады.
Итерация әдісінің жинақтылық коэффициенті 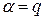 болып, жинақтылығы сызықты. Шынымен-ақ
болып, жинақтылығы сызықты. Шынымен-ақ
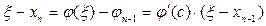 ,
,
бұл жерден 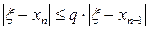 .
.
Ескерту. Түбір жатқан аймақтың әйтеуір бір аймағында 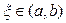 ,
, 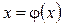 теңдеу және оның туындысы
теңдеу және оның туындысы 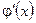 таңбасын сақтасын және
таңбасын сақтасын және 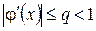 теңсіздік орындалсын. Онда, егер
теңсіздік орындалсын. Онда, егер 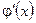 оң болса
оң болса 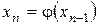 біртіндеп жуықтау түбірге монотонды жинақталады.
біртіндеп жуықтау түбірге монотонды жинақталады.
Егер 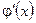 теріс болса, онда біртіндеп жуықтау түбірдің айналасында ауытқып жүреді. (сурет.9-ды қара).
теріс болса, онда біртіндеп жуықтау түбірдің айналасында ауытқып жүреді. (сурет.9-ды қара).
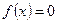 теңдеуді
теңдеуді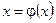 формада жазу тәсілін қарастырайық.
формада жазу тәсілін қарастырайық.
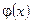 функцияны түбірдің төңірегінде
функцияны түбірдің төңірегінде 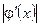 аз шама болатындай етіп беру керек.
аз шама болатындай етіп беру керек.
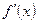 туындының ең кіші және ең үлкен мәндері -
туындының ең кіші және ең үлкен мәндері - 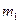 және
және 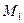 белгілі болсын.
белгілі болсын.
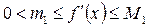 . (3.37)
. (3.37)
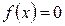 теңдеуді оған эквивалент
теңдеуді оған эквивалент 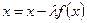 теңдеуімен алмастырайық.
теңдеуімен алмастырайық.
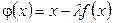 болсын. Түбір
болсын. Түбір 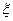 -дің төңірегінде
-дің төңірегінде 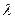 параметрді төмендегі теңсіздік орындалатындай етіп таңдаймыз.
параметрді төмендегі теңсіздік орындалатындай етіп таңдаймыз.
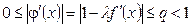 .
.
Бұл жерден (3.37)-ге байланысты
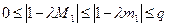 теңсіздікке ие боламыз.
теңсіздікке ие боламыз.
Онда 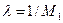 десек,
десек, 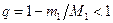 болады.
болады.
Білімін тексеру сұрақтары:
1. Берілген [a,b] кесіндіде түбірдің бар болуының қажетті шартын жазыңыз.
2. Берілген [a,b] кесіндіде жалғыз түбірдің бар болуының жеткілікті шартын жазыңыз.
3. Бір белгісізді теңдеулерді шешудің 1-ші этапын айтыңыз.
4. Бір белгісізді теңдеулерді шешудің 2-ші этапын айтыңыз.
5. Ньютон әдісінің геометриялық мағынасы қандай.
6. Біріккен тәсілдің геометриялық мағынасы қандай.
7. Итерациялық әдістің жинақтылығының жеткілікті шартын айтыңыз.
8. Ньютон әдісінің жинақтылығының жеткілікті шартын айтыңыз.
9. Ньютонның модификацияланған әдісінің жай әдістен айырмашылығы қандай?
10. Алғашқы теңдеуді итерациялық тәсілге қажетті түрге қалай келтіруге болады.?
