Раздел 4. Дифференциальное исчисление функции одной переменной
1. Производная. Геометрический и механический смысл.
2. Теорема о непрерывности дифференцируемой функции.
3. Основные правила дифференцирования.
4. Производная сложной функции.
5. Производные основных и элементарных функций.
6. Производная функции, заданной неявно.
7. Производная функции, заданной параметрически.
8. Логарифмическое дифференцирование.
9. Производные высших порядков.
10. Дифференциал функции, его свойства, геометрический смысл.
11. Применение дифференциала в приближенных вычислениях.
12. Дифференциалы высших порядков.
13. Теоремы Ролля, Лагранжа, Коши.
14. Раскрытие неопределенностей вида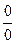 
(правило Лопиталя).
15. Раскрытие неопределенностей других видов по правилу Лопиталя.
16. Экстремумы функции. Необходимое условие экстремума (теорема Ферма).
17. Достаточное условие возрастания (убывания) функции.
18. Достаточные условия существования экстремума.
19. Выпуклость, вогнутость графика функции; достаточные условия.
20. Точки перегиба графика функции; достаточные условия.
21. Асимптоты графика функции.
22. Общая схема исследования функции и построения графика.
23. Наименьшее и наибольшее значения непрерывной на отрезке функции.
Раздел 5. Функции нескольких переменных
1. Функции двух и трех переменных как функции точки.
2. Геометрическое изображение функции двух переменных с помощью поверхностей и линий уровня.
3. Предел функции. Непрерывность в точке и в области.
4. Частные производные функции нескольких переменных; геометрический смысл частных производных функции двух переменных.
5. Полный дифференциал функции нескольких переменных.
6. Частные производные высших порядков.
7. Экстремум функции двух переменных. Необходимые условия экстремума.
8. Достаточные условия экстремума функции двух переменных.
9. Наибольшее и наименьшее значение функции в замкнутой ограниченной области.
10. Условный экстремум функции двух переменных. Экономический смысл множителей Лагранжа.
Раздел 6. Неопределенный интеграл
1. Первообразная. Неопределенный интеграл.
2. Таблица основных интегралов.
3. Основные свойства неопределенного интеграла.
4. Метод замены переменной в неопределенном интеграле.
5. Метод интегрирования по частям.
6. Интегралы от некоторых функций, содержащих квадратный трехчлен.
7. Интегрирование рациональных дробей.
8. Интегрирование иррациональных функций.
9. Интегрирование тригонометрических функций.
10. Вычисление интегралов вида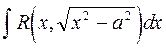 
, 
, 
.
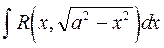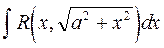11. Интегралы, не выражающиеся через элементарные функции.