Предмет начертательной геометрии
Лекция №1
В математическом энциклопедическом словаре дается следующее определение: «Начертательная геометрия – раздел геометрии, в котором пространственные фигуры, а также методы решения и исследования пространственных задач изучаются с помощью их изображений на плоскости».
Методы начертательной геометрии являются теоретической базой для решения задач технического черчения. В технике чертежи являются основным средством выражения человеческих идей. Они должны не только определять форму и размеры предметов, но и быть достаточно простыми и точными в графическом исполнении, помогать всесторонне исследовать предметы и их отдельные детали. Для того чтобы правильно выразить свои мысли с помощью рисунка, эскиза, чертежа требуется знание теоретических основ построения изображений геометрических объектов, их многообразие и отношения между ними, что и составляет предмет начертательной геометрии.
Изображение фигуры на плоскости как графический способ представления информации о ней имеет преимущества в сравнении с другими способами:
· общение становится более доступным, потому что образы, создаваемые на основе визуального (зрительного) восприятия, обладают большей, чем слова, ассоциативной силой;
· изображения являются интернациональным языком общения, тогда как, например, вербальное общение требует для понимания, как минимум знания языка собеседника.
Таким образом теоретические основы визуализации информации о геометрических объектах, многообразие геометрических объектов пространства, отношения между ними и их графического отображения на плоскости составляют предмет начертательной геометрии.
Задача этой науки – создание оптимальных геометрических форм объектов машиностроения, архитектуры и строительства, разработка теории графического отображения объектов и процессов.
Начертательная геометрия со времен ее основоположника Г. Монжа (1746-1818) завоевала свое достойное место в высшей школе как наука. Важнейшее прикладное значение начертательной геометрии как учебной дисциплины состоит в том, что она учит владеть графическим языком, выполнять и читать чертежи и другие изображения геометрических объектов, без чего немыслимо формирование инженера. Она обеспечивает преемственность между школьными курсами геометрии и черчения и графическими дисциплинами вуза.
Изучение начертательной геометрии способствует развитию пространственного воображения и навыков правильного логического мышления. Совершенствуя нашу способность - по плоскому изображению мысленно создавать представления о форме предмета и наоборот создание изображений мысленно созданных образов – визуализация мысли.
Однако не всякое изображение отображает геометрические свойства оригинала и не может быть принято для всестороннего его исследования. Принципиальное отличие методов изображения, изучаемых в курсе начертательной геометрии, от некоторых современных технических средств отображения (фотография, голография и др.), заключается в возможности с большой наглядностью и метрической достоверностью отобразить не только существующие предметы, но и возникающие в нашем представлении образы проектируемого объекта.
Изображение, которое позволяет определять взаимосвязь (взаимопринадлежность) элементов объекта, называют полным.
Изображения, по которым можно определить размеры объекта, называется метрически определенными.
Из плоскостных изображений объекта наиболее широкое применение в практике получили рисунки и чертежи. Рисунком называют изображение предмета от руки и на глаз с кажущимися относительными размерами и положениями отдельных его элементов. Чертежом называют изображение предмета, построенное по особым правилам с помощью чертежных инструментов в точной зависимости от размеров и положения в пространстве соответствующих линий предмета.
В технике чертежи являются основным средством выражения человеческих идей. Они должны не только определять форму и размеры предметов, но и быть достаточно простыми и точными в графическом исполнении, помогать всесторонне, исследовать предметы и их отдельные детали.
Эти требования к чертежам и привели к созданию теории изображений, составляющей основу начертательной геометрии. Правила построения изображений основаны на методе проекций. Поэтому проекционный метод построения изображений является основным методом начертательной геометрии
Итак, в курсе начертательной геометрии изучаются:
· методы отображения пространственных объектов на плоскости;
· способы графического и аналитического решения различных геометрических задач;
· приемы увеличения наглядности и визуальной достоверности изображений проецируемого объекта;
· способы преобразования и исследования геометрических свойств изображенного объекта;
· основы моделирования геометрических объектов.
Виды проецирования.
Одно из основных геометрических понятий - отображение множеств. В начертательной геометрии каждой точке трехмерного пространства ставится в соответствие определенная точка двумерного пространства – плоскости. Геометрическими элементами отображения служат точки, линии, поверхности пространства. Геометрический объект, рассматриваемый как точечное множество отображается на плоскость по закону проецирования. Результатом такого отображения является изображение объекта.
В основу любого изображение положена операция проецирования, которая заключается в следующем. В пространстве выбирают произвольную точку S (рис.1.1) в качестве центра проецирования и плоскость Пi, не проходящая через точку S, в качестве плоскости проекций ( картинной плоскости). Чтобы спроецировать точку А на плоскость Пi , через центр проецирования S проводят луч SА до его пересечения с плоскостью Пi в точке Аi. Точку Аi принято называть центральной проекцией точки А , а луч SА - проецирующим лучом.
Описанные построения выражают суть операции, называемой центральным проецированием точек пространства на плоскость.
В евклидовом пространстве существуют точки, которые не имеют центральных проекций, и наоборот в плоскости Пi есть точки, которые в пространстве не имеют оригиналов (точки D и F).
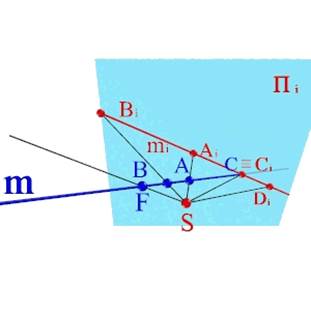 Точка F прямой m принадлежит плоскости , Ω, проходящей через центр проецирования S и расположенной параллельно плоскости проекций, таким образом проецирующий луч SF параллелен плоскости проекций, а точка F, как и все точки лежащие в плоскости Ω не имеют центральных проекций на Пi.
Точка F прямой m принадлежит плоскости , Ω, проходящей через центр проецирования S и расположенной параллельно плоскости проекций, таким образом проецирующий луч SF параллелен плоскости проекций, а точка F, как и все точки лежащие в плоскости Ω не имеют центральных проекций на Пi.
Рисунок 1.1. Центральное проецирование
Точка Di проекции прямой mi не имеет оригинала на прямой m, так как проецирующий луч SDi параллелен прямой.
Для исключения подобных случаев евклидово пространство расширяют введением несобственных (бесконечно удаленных) точек. Такое пространство называется расширенным евклидовым пространством.
Проецирующие лучи, проведенные через все точки кривой n, образуют проецирующую коническую поверхность N (рис. 1.2). Проекция криволинейной фигуры, таким образом, представляет собой линию пересечения проецирующей поверхности N и плоскости проекций Пi.
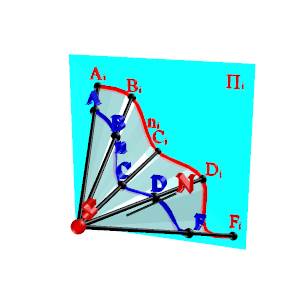
Рисунок 1.2. Центральное проецирование линии
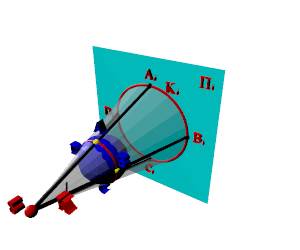
Рисунок 1.3. Центральное проецирование поверхности
Коническую поверхность К образуют лучи и при проецировании трехмерной фигуры (рис. 1.3). Линию Ki принято называть в этом случая очерковой или очерком данной фигуры.
Центральное проецирование есть наиболее общий случай проецирования геометрических объектов на плоскости.
Основными и неизменными его свойствами (инвариантами) являются следующие:
1) проекция точки – точка;
2) проекция прямой – прямая;
3) если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.
По принципу центрального проецирования работают фотоаппараты и кинокамеры. Упрощенная схема работы человеческого глаза близка к этому виду проецирования: роль центра проецирования выполняет оптический центр хрусталика, роль проецирующих прямых – лучи света; плоскостью проекций служит сетчатка глаза. Поэтому изображения, построенные по принципу центрального проецирования, наиболее наглядны и их широко используют в своей работе художники, архитекторы, дизайнеры и многие другие специалисты.
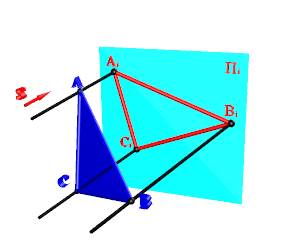
Рисунок 1.4. Параллельное проецирование
Частный случай центрального проецирования – параллельное проецирование, когда центр проецирования удален в бесконечность, при этом проецирующие лучи можно рассматривать как параллельные проецирующие прямые. Положение проецирующих прямых относительно плоскости проекций определяется направлением проецирования S (рис.1.4). В этом случае полученное изображение называют параллельной проекцией объекта.
При параллельном проецировании сохраняются свойства центрального и добавляются следующие:
проекции параллельных прямых параллельны между собой;
отношение отрезков прямой равно отношению их проекций;
отношение отрезков двух параллельных прямых равно отношению их проекций.
В свою очередь параллельные проекции подразделяются на прямоугольные, когда проецирующие прямые перпендикулярны плоскости проекций, и косоугольные, когда направление проецирования образует с плоскостью проекций угол не равный 900.
Таким образом ортогональное (прямоугольное) проецирование является частным случаем параллельного и полученная этим методом проекция объекта называется ортогональной.
Ортогональному проецированию присущи все свойства параллельного и центрального проецирования и кроме того, справедлива теорема о проецировании прямого угла: если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то прямой угол на эту плоскость проецируется в прямой угол.
К проекционным изображениям в начертательной геометрии предъявляются следующие основные требования:
1. Обратимость – восстановление оригинала по его проекционным изображениям (чертежу) – возможность определять форму и размеры объекта, его положение и связь с окружающей средой;
2. Наглядность – чертеж должен создавать пространственное представление о форме предмета;
3. Точность – графические операции, выполненные на чертеже, должны давать достаточно точные результаты;
4. Простота – изображение должно быть простым по построению и должно допускать однозначное описание объекта в виде последовательности графических операций.
