Построение эллипса по двум осям

Масштаби

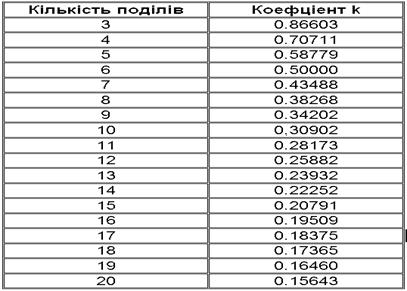
Масштабом називається відношення лі­нійних розмірів зображення, поданого на кресленні, до відповідних розмірів предме­та. Масштаби зображень на кресленнях слід вибирати з такого ряду (ГОСТ 2.302-68):

· масштаби зменшення—1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1000;

· натуральна (справжня) величина —1:1;

· масштаби збільшення —2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1.

Перевагу слід надавати зображенню предмета в натуральну величину.

Масштаб, указаний у призначеній для цього графі основного напису креслення, позначається так: 1:1; 1:2; 4:1 і т.д., а у всіх інших випадках — М1:1; М1:2; М4:1 і т.д.

------------------------------------------------------------------------------------------------------------------------------------------

4. Ро́змір — це числове значення лінійної величини (діаметр, довжина, висота та ін.).

За ДСТУ 3321-96 у системі конструкторської документації у поняття «розмір» вкладено два його види:

1. лінійний розмір — розмір виробу, поданий у лінійних одиницях виміру;

2. кутовий розмір — розмір виробу, поданий у кутових одиницях виміру.

· Номінальний розмір — розмір, відносно якого визначаються граничні розміри і який використовується для відліку відхилень. Номінальні розміри вибирають під час конструювання на основі розрахунків або за конструктивними міркуваннями і проставляють при кресленні деталі або з’єднанні деталей. Номінальні розміри після розрахунків округляють до найближчого з рядів нормальних лінійних розмірів згідно з ГОСТ 6636-69 [3], реалізованих на основі рядів переважних чисел.

· Дійсний розмір — це розмір, встановлений вимірюванням з допустимою похибкою.

· Граничні розміри — це два гранично допустимих розміри (найбільший і найменший), між якими повинен знаходитись дійсний розмір. На кресленні деталі або з’єднанні проставляють номінальні розміри, а кожний з двох граничних розмірів визначають по його відхиленнях від номінального. Різниця між граничними розмірами називається допуском.

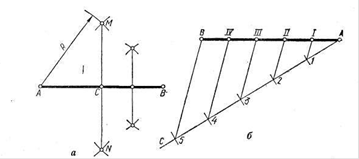
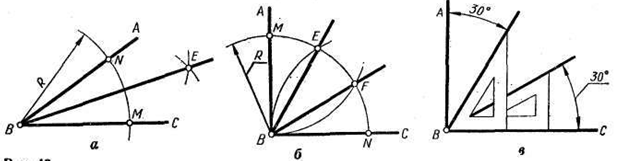
5. Ділення відрізка прямої та кутів

------------------------------------------------------------------------------------------------------------------------------------------

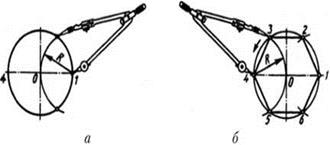
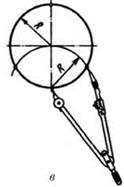6.Поділ кола на рівні частини

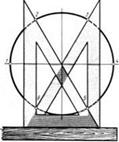
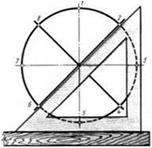
l = dk, де l - довжина хорди; d - діаметр заданої окружності;

------------------------------------------------------------------------------------------------------------------------------------------

7.Побудова нахилу і конусності

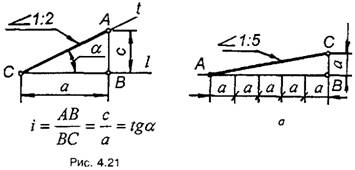Нахил однієї лінії відносно іншої, розта­шованої переважно горизонтально або вер­тикально, характеризує величину, яка нази­вається похилом.

Похил позначається на кресленні зна­ком 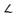(див. рис. 4.21). Щоб побудувати за­даний похил, наприклад 1:5, на горизон­тальній прямій відкладають п'ять рівних довільних відрізків а (рис. 4.22,а), які утво­рюють відрізок АВ. Потім з кінця В ставлять перпендикуляр ВС завдовжки а. Сполучив­ши точки С і А, отримують лінію, побудова­ну з похилом 1:5.

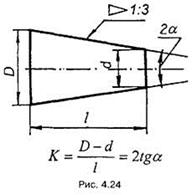Конусність визначають як відношення рі­зниці діаметрів двох поперечних перерізів ко­нуса до відстані між ними (рис. 4.24)

Конусність можна подати простим дробом або у відсотках.

Конусність позначається на кресленні зна­ком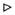

------------------------------------------------------------------------------------------------------------------------------------------

8.Сопряжение дуги с прямой

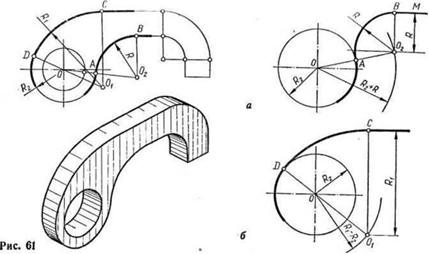
Различают случаи внешнего и внутреннего сопряжений прямой с дугой окружности.

Внешнее сопряжение. Для построения внешнего сопряжения (рис. 61, а) проводят вспомогательную прямую, параллельную прямой ВМ, на расстоянии, равном радиусу R дуги сопряжения. Из центра О радиусом R2 R проводят вспомогательную дугу. Точка Оа пересечения дуги со вспомогательной прямой является центром сопряжения. Пересечение линии центров 002 с окружностью дает точку сопряжения А; для получения точки сопряжения В восставляют перпендикуляр из центра 02 к прямой ВМ. Завершают построение проведением дуги радиусом R = 02В между точками А и В.

Внутреннее сопряжение. При внутреннем сопряжении (рис. 61, 6) совершают те же построения с той лишь разницей, что вспомогательную дугу проводят радиусом Rx — R2\ точка сопряжения D находится на пересечении продолжения линии центров OjO с окружностью.

------------------------------------------------------------------------------------------------------------------------------------------

9. Побудова овала по двум осям

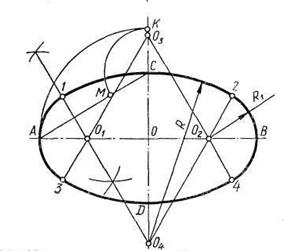
Построение овала по двум осям АВ и CD (рис. 63, в). На прямой, соединяющей точки Л и С, откладывают от точки С отрезок СМ, рав­ный разности полуосей овала, т. е. СМ — О К — ОС. Из середины отрезка AM восставляют перпендикуляр и продолжают его до пере­сечения с осями овала в точках и 0₄. Определяют симметричные им точки 0₂ и 0₃ и проводят линии центров 0,0„; ОА; 0.,0₃; 0₂0₄. Из центра 0₄ проводят дугу радиусом R = 0₄С до пересечения с линиями центров 0₄0i и 0ц0_г в точках 1 н 2. Аналогично находят точки сопря­жения <5 и 4. Замыкающие дуги овала проводят из центров 0₁ и 0_г ра­диусом R_t = 0-^А или R_l = 0₂В.

------------------------------------------------------------------------------------------------------------------------------------------

10. ЛЕКАЛЬНЫЕ КРИВЫЕ

Лекальными называются кри­вые, вычерчиваемые при помощи ле­кала по предварительно найденным точкам.

Лекала — это специальные линейки с криволинейными кромками. К лекальным кривым относят эллипс, параболу, гиперболу, циклоиду, эпольвенту, синусоиду и др. Лекаль­ные кривые широко применяются для очертаний различных техниче­ских деталей, например: профилен кулачков, кронштейнов, подвесок, зубчатых колес, фасонного инструмент;! н т. п.

Порядок вычерчиклнии лекальных кривых. Ііпачале по определенным правилам строят точки, принадлежащие длиной кривой. Желательно, чтобы расстояния между точками не превышали 15 мм. Получен­ные точки от руки соединяют плавной кривой, а затем обводят кривую по лекалу. Лекало прикладывают к кривой так, чтобы оно охватывало своим контуром не менее трех-четырех точек одновременно. При об­водке, однако, некоторый участок кривой оставляют не обведенным. Следующий участок лекала должен перекрывать ранее обведенный участок кривой и т. д. Этот прием обеспечивает плавность кривой и отсутствие на ней изломов. Начинать обводку рекомендуется с участ­ков наибольшей кривизны. На рис. 67 показано, как обводить кривую при помощи лекала. В большинстве случаев приходится пользоваться не одним, а несколькими лекалами, подбирая их так, чтобы участки кривых имели наибольшую шіанность, оті» '..нищую характеру дай­ной кривой.

------------------------------------------------------------------------------------------------------------------------------------------

Построение эллипса по двум осям

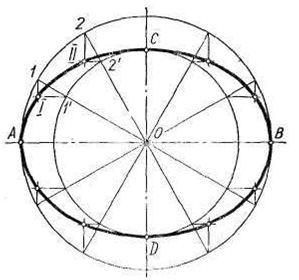Построение эллипса по большой АВ и малой CD осям (рис. 69, б). Из центра О эллипса проводят две концентрические окружности, диа­метры которых равны заданным осям АВ и CD. Большую окружность делят на равные части, например на 12, и точки деления соединяют с центром О. Проведенными радиусами малая окружность разделится на то же число равных частей. Из точек 1, 2, 3, ... большой окружности проводят вертикальные отрезки параллельно малой оси эллипса, а из точек 1', 2', 3', ... малой окружности — горизонтальные отрезки параллельно большой оси. Пересечение соответствующих отрезков дает точки эллипса 1, 11, 111, ... Полученные точки соединяют плавной кривой.

------------------------------------------------------------------------------------------------------------------------------------------

Метод проецирования

Проекционное черчение изучает способы построения на плоскости изображений предметов, имеющих три измерения. По этим изображе­ниям можно определять форму и величину предмета, взаимное расположение и размеры его составных частей, положение предмета относительно других предметов и изделий и т. п.

достаточно развитого пространственного мышления.

Для построения изображений предметов на плоскости пользуются методом проецирования.

Следовательно, проекция — это изображение предмета, «отбро­шенное на плоскость при помощи лучей. Спроецировать предмет на плоскость — это значит построить его изображение на плос­кости.

Проекции разделяют на центральные и параллельные.

------------------------------------------------------------------------------------------------------------------------------------------