Тема 4. Оптимизация и линейное программирование

4.1. Постановка задачи и классификация методов

Для исследования многих инженерно-технических и экономических процессов сначала составляют математическую модель в виде математической задачи, а затем используют численные методы для ее решения. Очень часто это приводит к необходимости решать задачу нелинейного программирования (НЛП), состоящую в нахождении таких значений переменных x=(x₁,x₂,…,x_n), при которых достигается минимум целевой функции

f(x₁,x₂…,x _n ) → min (4.1)

И выполняются ограничения:

g₁(x_1,x₂,…,x _n ) <0

g₂(x₁,x₂,…,x _n ) 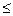0(4.2)

………

g_m(x₁,x₂,…x _n ) <0

где хотя бы одна функция f, g_1, g₂ ,…- нелинейная (возможны также ограничения в виде равенств). На переменные x могут быть наложены ограничения неотрицательности. Если все эти функции линейные, то мы имеем дело с задачей линейного программирования (ЛП), для решения которой разработаны специальные методы.

Функция (4.1) называется целевой. Вектор хназывается допустимым, если он удовлетворяет ограничениям (4.2). Вектор х называется оптимальным решением задачи (4.1)-(4.2), если хявляется допустимым и f(x₁,x₂,…,x_n) достигает минимума. Задача оптимизации может быть поставлена и на нахождение максимума целевой функции:

F(x₁,x₂,…,x_n) 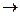max,

Но она легко может быть сведена к задаче (4. 1):

f(x₁,x₂,…,x_n)= - F(x₁,x₂,…x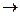_n) min

поэтому в дальнейшем будем рассматривать лишь задачу минимизации.

Термин “оптимальный” имеет латинское происхождение и означает “наилучший, наиболее благоприятный”. С математической точки зрения оптимизационная задача - это задача , в которой требуется найти оптимум (максимум или минимум) некоторой величины при выполнении каких-либо условий [6]. Переменные (x₁,x₂, …, x_n) могут быть конструктивными параметрами, установками регулятора, показаниями измерительных приборов и т.д., тогда как целевая функция может представлять собою стоимость, вес, годовой доход и т.д., а ограничения - технические требования, условия работы, пропускную способность…

В последнее время оптимизационные задачи привлекают особое внимание математиков. Разрабатываются новые численные методы оптимизации, хорошо приспособленные для реализации их с помощью компьютеров. Это вызвано, прежде всего, потребностями жизни, практики, постановками задач новых типов. На первый план выводят задачи, связанные с экономным расходом металла, энергии, увеличением прибыли и т.д., математическим образом которых и являются оптимизационные задачи. Разработкой методов решения подобных задач занимается область математики, называемая математическим програмированием. Однако до настоящего времени общих методов решения произвольной задачи НЛП не существует. Для различных классов задач, связанных с определенными видами целевой функции и структурой ограничений, разработаны разные классы методов:

- методы линейного программирования;

- методы динамического программирования (когда ограничения включат в себя как параметр время);

- методы выпуклого программирования ( когда целевая функция и функции ограничений выпуклы);

- методы стохастического программирования (когда в задаче есть вероятностный параметр);

- методы геометрического программирования;

- комбинаторные и эвристические методы.

Условно классификацию оптимизационных задач (и связанных с ними методов) можно провести следующим образом:

а) в зависимости от вида функции:

- линейные и нелинейные;

- выпуклые и невыпуклые;

б) по используемости в решении производных: - не использующие производные (метод покоординатного спуска);

- использующие 1 производную (градиентный метод);

- использующие 2 производную ( метод Ньютона);

в) в зависимости от наличия ограничений:

- задачи с ограничениями;

- задачи без ограничений;

г) в зависимости от количества переменных:

- c одной переменной;

- со многими переменными;

д) в зависимости от количества экстремумов:

- одноэкстремальные;

- многоэкстремальные.

Геометрически целевая функция (4.1) определяет собой поверхность, а ограничения (4.2) –допустимое множество решений n-мерного Эвклидова пространства (допустимую область - ДО).. Нахождение решения задачи нелинейного программирования сводится к нахождению точки из допустимого множества, в которой f(x) достигает экстремума (минимума). Решение может находиться либо внутри области, либо на ее границе. Следующая теорема дает необходимые и достаточные условия существования решения задачи.

Теорема. Если целевая функция непрерывна, а допустимое множество замкнутое, непустое и ограниченное, то решение задачи (4.1)-(4.2) существует.

Линейное программирование

Термин "линейное программирование" возник из неточного перевода английского словосочетания "linear programming" -"планирование на основе линейных соотношений" [13]. Теория ЛП занимается созданием методов, позволяющих оптимизировать линейную функцию, на которую наложены линейные ограничения. В основном задачи ЛП ставятся в теории планирования и управления экономическими процессами, реже - в технических задачах. С точки зрения классической математики подобные задачи представляют собой оптимизационные задачи на условный экстремум. Каноническая форма задачи ЛП выглядит следующим образом: найти

Z=c₁x₁+c₂x₂+...+c_nx_n → min (целевая функция)

при выполнении ограничений:

a₁₁x₁+a₁₂x₂+...+a_1nx_n=b₁

a₂₁x₁+a₂₂x₂+...+a_2nxn=b₂

......................…………..

a_m1x₁+a_m2x₂+...+a_mnx_n=b_m

на переменные могут быть также наложены ограничения неотрицательности:

x₁≥0, x₂≥0, ..., x_n≥0

Различные постановки задач ЛП могут приводить к разной математической записи (в ограничениях могут быть как знаки равенств, так и неравенств). Переход от разных формулировок к канонической записи нужен для того, чтобы пользоваться стандартными программами, реализованными на компьютерах (а они, в свою очередь, ориентированы на реализацию известного симплекс-метода решения задачи ЛП). Однако для использования графического метода решения лучше использовать стандартную форму записи, в которой ограничения представлены в форме нестрогих неравенств. Для анализа задача ЛП введем некоторые определения. Совокупность значений (х₁, х₂, …,х_n), удовлетворяющих ограничениям, называется допустимым (возможным) решением. Множество всех допустимых решений называют областью допустимых решений (ОДР). Допустимое решение, для которого целевая функция достигает максимума (или минимума), называется оптимальным. Используя приведенные определения, задачу ЛП можно сформулировать следующим образом: необходимо из совокупности допустимых решений выбрать то, которое соответствует минимуму целевой функции.

Пример постановки задачи ЛП:

Фабрика выпускает мороженое по 2 рецептам. Норма расхода исходных продуктов на 1 т мороженого, их запасы, себестоимость и цена представлены в таблице:

Продукты	Норма расхода на 1 т (в кг)	Запасы продуктов(кг)
	1 рецепт	2 рецепт
Молоко
Молоко сухое
Масло сливочное
Сахар
Себестоимость шт. ( в грн)	0,65	0,7
Продажная цена (в грн)		1,2

Необходимо найти такой план выпуска продукции, который обеспечит максимальную прибыль при имеющихся ресурсах. Обозначим х₁ - количество выпускаемого мороженого по 1 рецепту, х₂ - по 2-му рецепту. Задача формулируется в виде:

х₁(1-0.65) + х₂ (1,2-0,7)→max

650х₁ + 569х₂≤ З000

100x₁ + 50x₂≤5700

87х₁ + 120х₂≤ 13800

163х₁ +101x₂≤ 13500

Усложнение примера: по 1 рецепту должно быть выпущено не менее 15 тн, а по 2-му - не менее 45 тн:

х₁≥15, х₂≥45

Усложнение примера: максимальное время работы фасовочного автомата 400 часов, автомат расфасовывает 1 тн мороженого за 4,5 часа:

4,5 (х₁ + х₂)≤400

Для перехода от одного вида записи зада ЛП к другой необходимо использовать следующие приемы:

1)переход от задачи максимизации к минимизации и наоборот:

z₁=c₁x₁+c₂x₂+...+c_nx_n → max

z₂= -z₁=-c₁x₁-c₂x₂-...-c_nx_n → min

2) переход от ограничений-неравенств к равенствам. Для этого в задачу вводится дополнительная переменная x_n+1, которая является фиктивной и в целевую функцию входит с коэффициентом нуль:

a₁₁x₁+a₁₂x₂+...+a_1nx_n≤b₁ → переход к

a₁₁x₁+a₁₂x₂+...+a_1nx_n+x_n+1=b₁

3) представление ограничения-равенства в виде неравенства. В этом случае равенство представляется в виде двух неравенств, т.е. увеличивается размерность задачи:

a₁₁x₁+a₁₂x₂+...+a_1nx_n=b₁ → переход к

a₁₁x₁+a₁₂x₂+...+a_1nx_n≤b₁

a₁₁x₁+a₁₂x₂+...+a_1nx_n≥b₁

4)переход от переменных, ограниченных снизу, к неотрицательным переменным:

x_i ≥ b_i→

заменив x_i = y_i + b_i, получим y_i ≥0

5) наложение на переменные ограничения неотрицательности, если это условие не выполняется. Для этого необходимую переменную х_j представим в виде разности двух новых переменных:

х_j = х_j'- х_j''_, х_j' _{≥ 0 ,} х_j '' _{≥ 0.}

С помощью таких приемов можно привести задачу ЛП к канонической или стандартной форме.

Для точного решения задачи ЛП применяется симплекс-метод, разработанный советским математиком Л.В.Канторовичем и американским Дж.Данцигом [8,11]. Основная идея метода состоит в нахождении точки пересечения n линейно независимых гиперплоскостей, задаваемых ограничениями-равенствами, и последовательном переходе к другой точке с уменьшением целевой функции. Такие точки можно представить вершинами некоего многогранника, являющегося пересечением конечного числа полупространств - допустимых решений. Главное преимущество симлекс-метода - универсальность и простота реализации на компьютере