Математические модели регуляторов
Остановимся на рассмотрении наиболее распространенных математических моделях линейных регуляторов по отклонению непрерывного действия [2]. В этих простейших законах управляющее воздействие 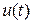 линейно зависит от сигнала ошибки
линейно зависит от сигнала ошибки 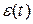 (включение в прямую цепь усилителя), его интеграла (включение интегрирующих звеньев) и первой производной (включение дифференцирующих звеньев). Сказанное выше позволяет ввести в рассмотрение следующие виды управляющих устройств (регуляторов):
(включение в прямую цепь усилителя), его интеграла (включение интегрирующих звеньев) и первой производной (включение дифференцирующих звеньев). Сказанное выше позволяет ввести в рассмотрение следующие виды управляющих устройств (регуляторов):
1) пропорциональное управляющее устройство (П - управление)
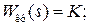 (3.2)
(3.2)
2) интегральное управляющее устройство (И - управление)
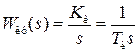 ,
, 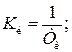 (3.3)
(3.3)
3) пропорционально-интегральное управляющее устройство (ПИ - управление)
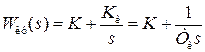 ; (3.4)
; (3.4)
4) пропорционально-дифференциальное управляющее устройство (ПД - управление)
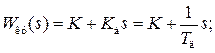 (3.5)
(3.5)
5) пропорционально – интегрально - дифференциальное управляющее устройство (ПИД - управление)
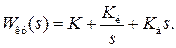 (3.6)
(3.6)
Вводя кратное интегрирование и дифференцирование, можно получить более сложные законы управления.
Приведем конкретные примеры использования регуляторов с указанными математическими моделями. При решении задач стабилизации целесообразно использовать П - управление, ПД - управление, цепи с ОС:
1. Стабилизация при помощи интегрирующего звена (П - управление) применяется, когда считают возможным сохранить в стабилизированной системе тот же порядок величины времени установления выходного сигнала и тот же порядок величины частоты среза, которые были в нестабилизированной системе. Напомним, что время установления выходного сигнала определяется как такое время 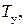 в течение которого выходная величина возросла бы от 0 до 1, если бы скорость ее роста была постоянна и максимальна. Для вычисления
в течение которого выходная величина возросла бы от 0 до 1, если бы скорость ее роста была постоянна и максимальна. Для вычисления 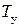 можно пользоваться формулами
можно пользоваться формулами
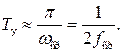
2. Стабилизация при помощи дифференциального звена (ПД - управление) применяется для улучшения работы системы на всех частотах. При применении этого метода происходит, в частности, повышение частоты среза и соответствующее уменьшение времени установления выходной величины. При этом обычно увеличивается допустимый коэффициент усиления по скорости и сохраняется удовлетворительный запас устойчивости, т.е. достаточное значение избытка фазы в окрестности точки, соответствующей частоте среза.
3. Стабилизация при помощи одной или нескольких дополнительных цепей обратной связи применяется для улучшения характеристик системы. Этот метод стабилизации систем весьма эффективен. Кроме того, он позволяет уменьшить влияние изменений (флюктуаций) параметров некоторых ее элементов на поведение системы.
