Оценка надежности результатов множественной регрессии и корреляции

Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью 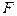-критерия Фишера:

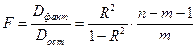
где 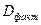– факторная сумма квадратов на одну степень свободы;

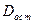– остаточная сумма квадратов на одну степень свободы;

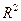– коэффициент (индекс) множественной детерминации;

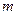– число параметров при переменных 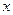(в линейной регрессии совпадает с числом включенных в модель факторов);

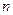– число наблюдений.

Пример. Предположим, что модель урожайности пшеницы 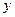(ц/га) от количества внесенных минеральных удобрений на 1 га 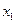(ц) и осадков 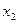(мм) характеризуется следующим уравнением;

.

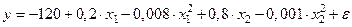При этом 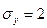, , 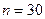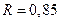. Результаты дисперсионного анализа оказываются следующими (см. табл.).

Результаты дисперсионного анализа

Источники вариации	Число степеней свободы	Сумма квадратов,	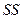Дисперсия на одну степень свободы,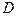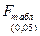
Объясненная за счет регрессии		86,7	21,675	16,27	2,76
Остаточная		33,3	1,332	1,00	–
Общая		120,0	–	–	–

;

;

.

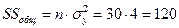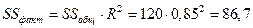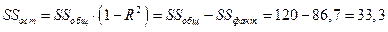Так как фактическое значение 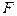-критерия при 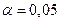превышает табличное, то уравнение статистически значимо. Этот же результат получим, воспользовавшись приведенной ранее формулой 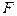-критерия:

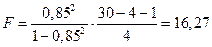
Оценивается значимость не только уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель. Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличивать долю объясненной вариации результативного признака. Кроме того, при наличии в модели нескольких факторов они могут вводиться в модель в разной последовательности. Ввиду корреляции между факторами значимость одного и того же фактора может быть разной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частный 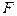-критерий, т. е. .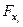

Частный 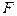-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом.

В общем виде для фактора 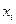частный 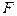-критерий определится как

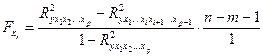
Предположим, что оцениваем значимость влияния 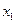как дополнительно включенного в модель фактора. Используем следующую формулу:

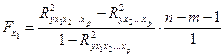
где 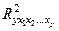– коэффициент множественной детерминации для модели с полным набором факторов;

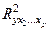– тот же показатель, но без включения в модель фактора ;

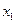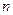– число наблюдений;

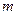– число параметров в модели (без свободного члена).

Если оцениваем значимость влияния одного фактора после включения в модель факторов другого для линейной двухфакторной регрессии, то формула частного 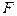-критерия примет вид:

;

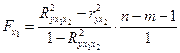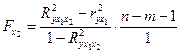
В числителе формул (2) – (4) показан прирост доли объясненной вариации 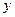за счет дополнительного включения в модель соответствующего фактора.

В знаменателе доля остаточной вариации по регрессионной модели, включающей полный набор факторов.

Фактическое значение частного 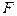-критерия сравнивается с табличным при 5%-ном или 1%-ном уровне значимости и числе степеней свободы: 1 и 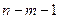. Если фактическое значение превышает табличное, то дополнительное включение фактора 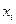в модель статистически оправданно и коэффициент чистой регрессии 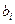при факторе 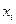статистически значим. Если же фактическое значение 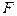-критерия меньше табличного, то дополнительное включение в модель фактора 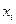не увеличивает существенно долю объясненной вариации признака 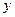, следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.

С помощью частного 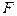-критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор 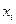вводился в уравнение множественной регрессии последним.

Частный 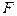-критерий оценивает значимость коэффициентов чистой регрессии. Зная величину 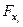, можно определить и 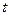-критерий для коэффициента регрессии при 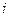-м факторе, 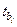, a именно:

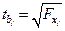
Оценка значимости коэффициентов чистой регрессии по 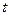-критерию Стьюдента может быть проведена и без расчета частных 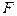-критериев. В этом случае, как и в парной регрессии, для каждого фактора используется формула

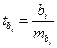
где 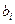– коэффициент чистой регрессии при факторе ;

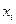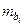– средняя квадратическая ошибка коэффициента регрессии .

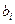Для уравнения множественной регрессии

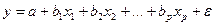
средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле:

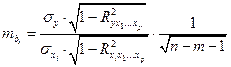
где 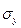– среднее квадратическое отклонение для признака ;

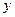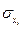– среднее квадратическое отклонение для признака _;;

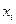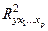– коэффициент детерминации для уравнения множественной регрессии;

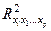– коэффициент детерминации для зависимости фактора 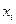, со всеми другими факторами уравнения множественной регрессии.

Как видим, чтобы воспользоваться данной формулой, необходимы матрица межфакторной корреляции и расчет по ней соответствующих коэффициентов детерминации 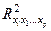. Так, для уравнения

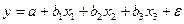
оценка значимости коэффициентов регрессии 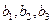предполагает расчет трех межфакторных коэффициентов детерминации, а именно: , , .

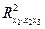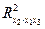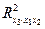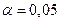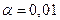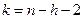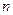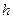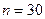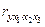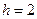Аналогично можно оценивать и существенность частных показателей корреляции. Фактическое значение частного коэффициента корреляции сравнивается с табличным значением при или и числе степеней свободы , где – число наблюдений, – число исключенных переменных. Так, если и оценивается существенность частного коэффициента корреляции второго порядка (например, ), то и .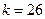

Если 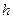является наивысшим порядком расчета частных коэффициентов корреляции для уравнения регрессии, то практически величина 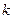совпадает с числом степеней свободы для остаточной вариации с 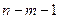. Если же уравнение регрессии дополняется расчетом частных коэффициентов корреляции разных порядков (второго, третьего и т. п.), то

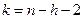
Если величина частного 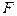-критерия выше табличного значения, то это означает одновременно не только значимость рассматриваемого коэффициента регрессии, но и значимость частного коэффициента корреляции. Существует взаимосвязь между квадратом частного коэффициента корреляции и частным 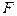-критерием, а именно:

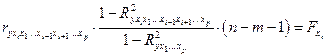
Взаимосвязь показателей частного коэффициента корреляции, частного F-критерия и
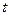-критерия Стьюдента для коэффициентов чистой регрессии может использоваться в процедуре отбора факторов. Отсев факторов при построении уравнения регрессии методом исключения практически можно осуществлять не только по частным коэффициентам корреляции, исключая на каждом шаге фактор с наименьшим незначимым значением частного коэффициента корреляции, но и по величинам 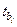и 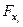. Частный 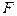-критерий широко используется и при построении модели методом включения переменных и шаговым регрессионным методом.