Дослідження загального рівняння площин

Розглядаються частинні випадки розміщення площин

,

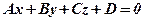коли деякі із чисел 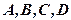дорівнюють нулю.

1. Якщо 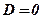, то рівняння має вигляд 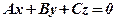, площина проходить через початок координат 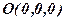перпендикулярно вектору .

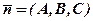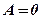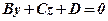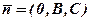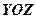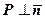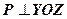2. Якщо , то маємо рівняння , вектор належить площині . Оскільки площина , то , або ж 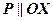. (див. рис.14). Рівняння площини 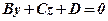є рівнянням сліда в площині .

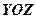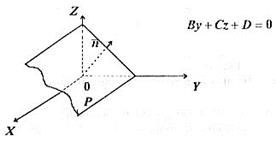
Рис. 14.

3. Якщо ж 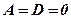, то площина 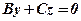проходить через вісь .

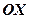4. Якщо 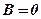, то рівняння площини має вигляд 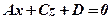, 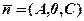належить площині 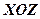. Площина 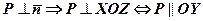(див. рис. 15).

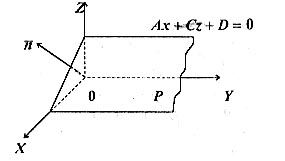
Рис. 15.

5. Якщо ж 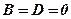, то площина 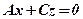проходить через вісь .

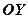6. Якщо 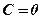, то маємо рівняння 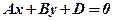, , 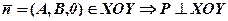або ж 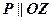(див. рис. 16)

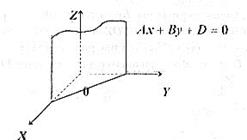
Рис. 16.

7.Якщо ж 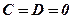, то площина 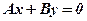проходить через вісь .

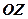Висновок. На основі 2, 4 і 6 отримуємо, що площина паралельна тій координатній осі, змінна якої в рівнянні відсутня.

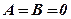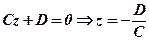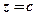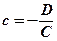8. , площина , або ж , де . Вектор 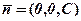напрямлений вздовж осі 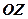, тому площина перпендикулярна до осі 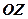в точці (0,0, 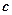). (див. рис. 17).

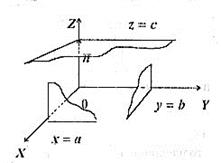
Рис. 17.

Зокрема, якщ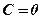о , то 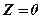– рівняння координатної площини .

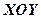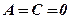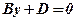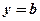9. Якщо , то маємо площину , або , де 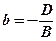. Вектор 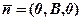напрямлений вздовж осі 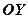. Площина перпендикулярна осі 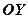в точці (0, 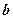,0). (див. рис. 17).

Зокрема, якщ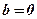о , то 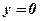– рівняння координатної площини .

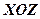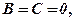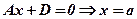10. На кінець, якщо то , де 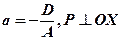(рис. 17).

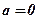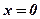При маємо – рівняння координатної площини .

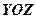Задача 1. Побудувати тіло. Обмежене площинами:

.

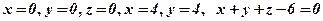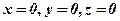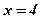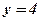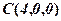Розв’язання. Для виконання побудови, необхідно побудувати кожну з площин окремо, знайти їх лінії перетину – ребра многогранника, та координати вершин. Площини – координатні, лініями їх перетину є осі координат. Площини і перпендикулярні осям і відповідно в точках і 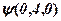(див. рис. 18).

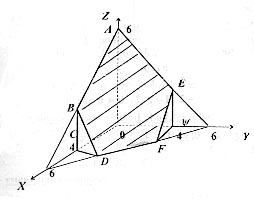
Рис. 18.

Площина 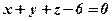відтинає на осях координат відрізки по 6 одиниць. В точці 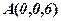ця площина перетинається з віссю 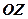, 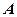– вершина многогранника. 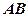– слід на площині 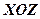, його рівняння 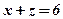, перетинається із слідом 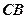, рівняння 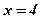. Звідки знаходимо координати точки 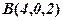. Аналогічно знаходимо інші вершини: .

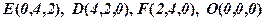Задача 2.За рівнянням 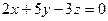побудувати площину.

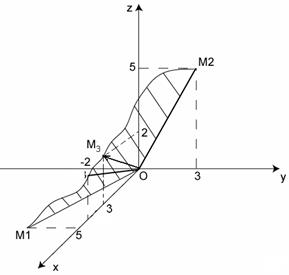
Розв’язання.Оскільки в даному рівнянні вільний член 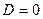, то площина проходить через точку О(0,0,0). Для кращого уявлення про положення даної площини побудуємо її сліди на координатних площинах ХОУ, YOZ і XOZ.

В площині ХОУ (z=0) слідом буде пряма 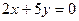, яка, крім точки О(0,0,0), проходить також, наприклад, через точку М₁(5,-2,0). Будуємо слід ОМ₁.

В площині YOZ (х=0) слідом буде пряма 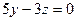, позначимо її ОМ₂, де М₂(3,5,0).

В площині XOZ (у=0) будуємо слід ОМ₃, який описується рівнянням 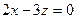і проходить через точку М₃(3,0,2). На малюнку заштрихована частина площини 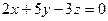, яка проходить через сліди ОМ₁, ОМ₂ і ОМ₃.