Лабораторная работа № 2. Модель парной регрессии. Метод наименьших квадратов
Цель: изучить возможности электронной таблицы Excel по обработке парной линейной регрессии.
Основные формулы и понятия:
у = a + b×х + u — модели парной линейной регрессии;
y = а + b×x — уравнение линейной регрессии;
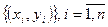— значение наблюдений;
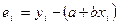— остаток в i-м наблюдении;
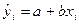— расчетное значение у в i-м наблюдении (точечный прогноз);
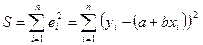) — суммы квадратов остатков;
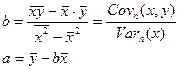— уравнения для параметров регрессии;
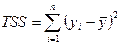— общая сумма квадратов отклонений;
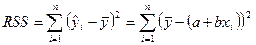— объясненная сумма квадратов отклонений;
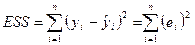— необъясненная (остаточная) сумма квадратов отклонений;
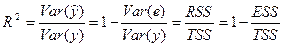— коэффициент детерминации.
Для парного регрессионного анализа выполняется условие: коэффициент детерминации R2 равен квадрату коэффициента корреляции, то есть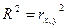 
Электронная таблица MS Excel
Ранее изученных нами статистических функций вполне достаточно для непосредственного вычисления коэффициентов регрессии. Для нахождения значения параметра b достаточно уметь вычислять значение ковариации и дисперсии, а для значения a необходимы также средние значения. Эти параметры можно легко найти самостоятельно, однако в электронной таблице Excel имеется много достаточно разнородных инструментов для определения параметров регрессии. Среди них, что совершенно очевидно, имеются статистические функции, а также дополнительные средства — это надстройка и средства точечных диаграмм. Начнем рассмотрение со статистических функций.
Функция НАКЛОНвозвращает наклон (коэффициент b в уравнении линейной регрессии). При этом аргументами являются два массива, в первом из которых задаются значения зависимой переменной y, а во втором значения регрессора x.
Значение коэффициента a может быть найдено либо по соответствующей формуле, либо при помощи функции ОТРЕЗОК, которая имеет подобные аргументы.
Функция ПРЕДСКАЗ вычисляет или предсказывает будущее значение по произвольному значению x. Данная функция имеет три аргумента. Первый — это значение x, а остальные имеют тот же смысл, что и в функциях НАКЛОН и ОТРЕЗОК.
К сожалению, нет специальных функций для вычисления коэффициента детерминации, а делать это на основании исходных формул достаточно затруднительно. Однако можно использовать то свойство, что коэффициент детерминации равен квадрату коэффициента корреляции.
Предположим, что исходные данные также располагаются в таблице 1, тогда в документ Excel параметры регрессии можно вычислить на основании следующих формул:
| b= | = КОВАР(C2:C16;B2:B16)/ДИСПР(B2:B16) |
| b= | =НАКЛОН(C2:C16;B2:B16) |
| a= | = СРЗНАЧ(C2:C16)- НАКЛОН(C2:C16;B2:B16)* СРЗНАЧ(B2:B16) |
| a= | =ОТРЕЗОК(C2:C16;B2:B16) |
| R2= | =КОРРЕЛ(C2:C16;B2:B16)* КОРРЕЛ(C2:C16;B2:B16) |
| Прогноз при x=17 | =ПРЕДСКАЗ(17;C2:C16;B2:B16) |
В данном случае предлагаются два способа вычисления параметров: на основании формул НАКЛОН и ОТРЕЗОК и через исходные формулы для параметров регрессии.
Вычисленные на основании этих формул значения будут равны:
b = –7,703
a = 239,96
R2 = 0,7868.
При цене, равной 17, прогнозируемый спрос будет равен 109,014.
Анализируя полученные данные, можно прийти к следующим выводам:
Поскольку b = –7,703, то можно предполагать, что увеличение цены на единицу в среднем уменьшает спрос на –7,703 тысячи штук, аналогично уменьшение цены на единицу увеличит спрос на –7,703 тысячи штук.
Значение константы в регрессионной модели равно 239,96, следовательно, именно такой должен быть спрос при цене равной нулю. Однако данное значение является во многом теоретическим и показывает только точку пересечения линии регрессии с осью oy.
Регрессионная модель имеет вид: y = 239,96 – 7,703x.
Прогнозируемый спрос при цене равной 17 будет составлять 109,014 тысячи единиц.
Коэффициент детерминации равен 0,7868. Данное значение может быть интерпретировано следующим образом: изменение зависимой переменной, в данном случае y на 78 %, описывается изменением независимой переменной (регрессора) x, что говорит о достаточной обоснованности использования данной модели.
Замечание. Описанные выше функции возвращают один параметр линейной регрессии. Однако имеется функция, которая одновременно возвращает оба параметра. Это функция ЛИНЕЙН(). Более подробно с данной функцией можно ознакомится по справочной системе.
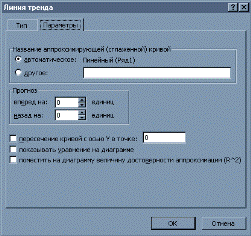
Кроме указанных функций в Excel имеется возможность построить на диаграмме линию регрессии, которая называется линией линейного тренда. Для этого необходимо задать точечную диаграмму (диаграмма обязательно должна быть точечной), и выбрав произвольную точку в контекстном меню, можно выбрать пункт Добавить линию тренда. Хотя термин «тренд» имеет несколько другой смысл, применительно к временным рядам, в данном случае термины «тренд» и «линия регрессии» будем отождествлять друг с другом. Выбор пункта Добавить линию тренда приведет к появлению диалогового окна, у которого имеются две закладки — Тип и Параметры (рисунок 6).
| |||
| |||
Рисунок 6 Построение линий тренда
На закладке Тип необходимо выбрать один из возможных видов уравнения регрессии. Если на диаграмме имеется несколько рядов точек, то линию регрессии можно построить для любой, задав значение соответствующего параметра — Построить на ряде.
На закладке Параметры можно задать дополнительную информацию, которая будет присутствовать на диаграмме. Во-первых, это возможность прогнозирования, что позволит построить линии тренда вперед или назад на соответствующее число единиц. Опция Показывать уравнение на диаграмме позволяет выдавать вид уравнения, а опция Поместить на диаграмму величину достоверности аппроксимации (R^2) выводит значение коэффициента детерминации. Построив точечную диаграммы для данных, заданных в таблице 1, и линию тренда, можно получить диаграмму, которая изображена на рисунке 7.
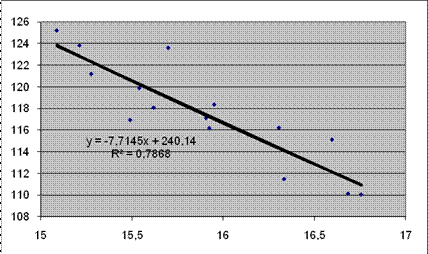
Рисунок 7 Линия тренда
В данном случае результаты полностью совпадают с полученными ранее посредством статистических функций.
Использование встроенных функций, да и точечных диаграмм, имеет определенные ограничения, поскольку нет функций, вычисляющих стандартные отклонения коэффициентов регрессии и значение детерминации. Поэтому рассмотрим дополнительные возможности, которые доступны с помощью надстройки Анализ данных. Данная надстройка подключается с помощью пункта меню Сервис, Надстройки и запускается на выполнение с помощью пункта меню Сервис, Анализ данных. После выбора надстройки Регрессияпоявится диалоговое окно (рисунок 8).
Данное диалоговое окно имеет множество дополнительных переключателей, которые приводят к выводу большого количества дополнительной информации.
Основные параметры, которые необходимо задать — это Входной интервал Y и Входной интервал X, а также Параметры вывода. Если количество данных Y и X совпадает, то выдаются итоги построения модели парной регрессии (именно этот случай будем сейчас рассматривать), а если число переменных X в несколько раз больше числа Y, то — модель множественной регрессии. В противном случае будет выдано сообщение об ошибке.
Если активизировать переключатель Метки, то во входные интервалы для X и Y можно добавить ячейки с названиями, и соответствующие метки появятся в итоговой таблице, что значительно облегчит её понимание.
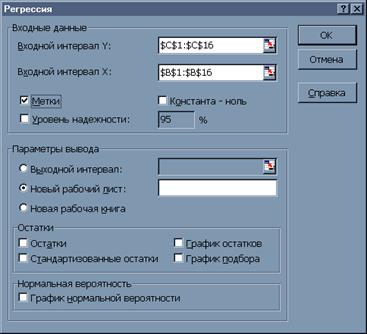
Рисунок 4 Окно Регрессия
Если Входной интервал Y определить как C1:C16, а Входной интервал X — B1:B16, задать некоторым образом параметры вывода, а также установить опцию Метки, то автоматически на новом листе будет сгенерированна таблица 4.
Таблица 4 Итоговая таблица
| ВЫВОД ИТОГОВ | |
| Регрессионная статистика | |
| Множественный R | 0,887036 |
| R-квадрат | 0,786833 |
| Нормированный R-квадрат | 0,770435 |
| Стандартная ошибка | 2,264609 |
| Наблюдения |
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 246,0889 | 246,0889 | 47,985 | 1,04E–05 | ||
| Остаток | 66,66991 | 5,128455 | ||||
| Итого | 312,7588 | |||||
| Коэффициенты | Стандартная ошибка | t- статистика | P- значение | Нижние 95 % | Верхние 95 % | |
| Y-пересечение | 240,142 | 17,70861 | 13,56075 | 4,76E–09 | 201,8849 | 278,3991 |
| Цена x (т.) | –7,71453 | 1,113671 | –6,92712 | 1,04E–05 | –10,1205 | –5,30859 |
Данная таблица содержит большое количество информации, поэтому будем изучать её содержимое постепенно, в нескольких последующих работах. Представленные в этой таблице данные можно условно разделить на три раздела:
¾ регрессионная статистика
¾ дисперсионный анализ
¾ коэффициенты.
Весь раздел регрессионная статистика посвящен описанию коэффициента детерминации и его различным характеристикам. В пунктах множественный R и R-квадрат выводится значение коэффициента детерминации и его квадрата. Пункты меню нормированный R-квадрат и стандартная ошибка будут нами рассмотрены позднее, при изучении множественной регрессии. Кроме этого выдается общее количество наблюдений.
Рассмотрим раздел дисперсионный анализ.
В столбце SS выдаются все виды сумм квадратов отклонений. В данном случае в первой строке, которая соответствует надписи Регрессия, выдается объясненная сумма квадратов отклонений RSS,
В строке — Остаток — выдается необъясненная (остаточная) сумма квадратов отклонений ESS,
В строке — Итого — выдается общая сумма квадратов отклонений TSS.
В последнем разделе, который не имеет названия, будет интерпретироваться как раздел — коэффициенты, содержится полная информация по коэффициентам. Рассмотрим значения, полученные в столбце Коэффициенты. Пункт Y-пересечение выдает значение коэффициента a. Пункт Цена x (т.) выдает значение коэффициента b.
Представленные в таблице значения полностью совпадают с данными, полученными посредством статистических функций и линий тренда на точечной диаграмме.
В диалоговом окне Регрессияимеется целый раздел переключателей для получения дополнительной информации по остаткам. Например,указав опцию Остатки, наряду со стандартной таблицей регрессии будет выдана дополнительная таблица (табл. 5) следующего вида:
Таблица 5 Дополнительная таблица
| ВЫВОД ОСТАТКА | ||
| Наблюдение | Предсказанное Спрос y (тыс. шт.) | Остатки |
| 123,7511 | 1,426776 | |
| 122,7896 | 1,019821 | |
| 122,2914 | –1,11646 | |
| 120,6462 | –3,7319 | |
| 120,2544 | –0,39014 | |
| 119,6494 | –1,5813 | |
| 119,0288 | 4,559903 | |
| 117,4316 | –0,34387 | |
| 117,2931 | –1,12322 | |
| 117,0864 | 1,257187 | |
| 114,353 | 1,847847 | |
| 114,1298 | –2,67328 | |
| 112,0989 | 3,003645 | |
| 111,4176 | –1,31194 | |
| 110,8662 | –0,84306 |
В данной таблице получены результаты предсказанных значений и значения остатков отдельно для каждого наблюдения. Указав опции График подбора, График остатков и График нормального распределения можно получить множество дополнительной информации и некоторые диаграммы.
Использование трех описанных нами инструментов исследования можно рассматривать как последовательные шаги в изучении парной регрессионной модели. При использовании статистических функций можно получить только уравнение регрессии и некоторый прогноз. Использование точечной диаграммы позволяет сразу увидеть уравнение регрессии, а также получить значение коэффициента детерминации. Точечная диаграмма может позволить и визуально оценить точность построенной модели. И, наконец, надстройка — Регрессия. Используя данный инструмент можно получить полную информацию относительно регрессионной модели. Данная таблица достаточно громоздкая, могут появиться затруднения с интерпретацией полученных результатов. Поэтому рекомендуется начинать исследование модели с использования статистических функций и линии тренда на точечной диаграмме.