Методы вычисления определителей

Высшая алгебра.

Матрица

Матрицей называется прямоугольная таблица чисел, например

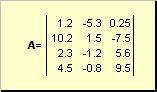
Матрицы обозначаются заглавными полужирными буквами (A), а их элементы — соответствующими строчными буквами с индексами, т.е. a_ij. Первый индекс нумерует строки, а второй — столбцы. В хемометрике принято обозначать максимальное значение индекса той же буквой, что и сам индекс, но заглавной. Поэтому матрицу A можно также записать как { a_ij, i = 1,..., I; j = 1,..., J}. Для приведенной в примере матрицы I = 4, J = 3 и a₂₃ = −7.5.

Пара чисел I и J называется размерностью матрицы и обознается как I×J.

Виды матриц

1) Матрица-строка: ;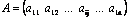

2) Матрица-столбец: 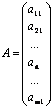; 3) Нулевая матрица: ;

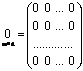4) Квадратная матрица – если 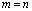(например n = 2): ;

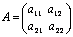5) Диагональная матрица (напр. 3-го порядка, где 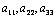любые числа ): ;

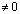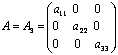6) Единичная матрица (например, 3-го порядка)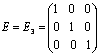

Операции над матрицами.

Пусть даны матрицы A = (аij)mxn и B = (bij)mxn.

1. Равенство матриц.

А = В тогда и только тогда, когда aij = bij (i = 1, m; j = 1, n).

Сложение матриц.

Суммой матриц А+В называется матрица С = А + В, где cij = aij + bij (i = 1, m; j = 1, n). Из определения операции сложения следуют свойства:

а) А + В = В + А.
б) (А + В) + С = А + (В + С).

Умножение матрицы на число l.

В = l · А, где bij = laij (i = 1, m; j = 1, n), т. е. каждый элемент матрицы А умножается на число l.

Произведение строки на столбец.

Если a = (a1 a2 ... an) и , то ab = a1b1 + a2b2 + ... + anbn.

Произведение матриц.

Если А = (аij)mxp и B = (bij)pxn, то матрица С = А·В = (сij)mxn, где – произведение i-той строки матрицы А на j-тый столбец матрицы В.

Замечание. Произведение А·В определено, если число столбцов матрицы А равно числу строк матрицы В.

Из определения операции умножения следует, что в общем случае А·В № В·А. Если А·В = В·А, то матрицы А и В называются коммутативными (перестановочными).

Свойства операции умножения матриц.

а) А·0 = 0·А = 0.
б) А·Е = Е·А = А.
в) (А+В)·С = А·С + В·С.
г) А(В + С) = А·В + А·С.
д) (А·В)·С = А·(В·С).

Определитель матрицы

это сумма всевозможных произведений элементов матрицы по одному элементу из каждой строки и столбца, с учетом знака. (в силу отсутствия острой необходимости, и громоздкости общей формулы, она не будет приведена, вместо это предлагается ипользовать методы описанные ниже, т.к. они проще и удобней)

Из определения видно, что опредилетель матрицы является вещественным числом.

Свойства определителя

Определитель , имеющий строку, представленной суммой двух строк, равносилен сумме определителей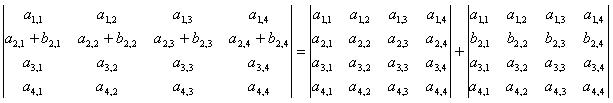

 Определитель , имеющий нулевую строку, равен нулю

 Определитель , имеющий две пропорцинальных строки , равен нулю

 Определитель единичной матрицы равен единице

 Опредилетель транспонированной матрицы равен определителю не транспонированной матрицы

 Определитель не изменится, если из строки вынести множитель

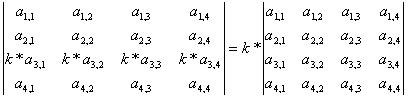
 Определитель не изменится, если одну из его строк домножить на число и добавить к другой cтроке

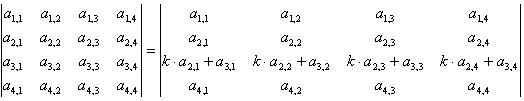
(в силу свойства 3)

 При перестановке двух строк определителя, определитель меняет знак

Определитель обозначается - det ( determinant ) или

Методы вычисления определителей.

1). Разложение по строке или столбцу.

2). Метод обращения в нуль всех, кроме одного, элементов строки или столбца. Метод состоит в том, что с учетом свойств определителя при помощи какого-либо столбца (строки) путём умножения его на соответствующие числа и вычитания из остальных столбцов (строк), зануляются все элементы выбранной строки (столбца) кроме одного, принадлежащего вычитаемому столбцу (строке).

3). Метод приведения к треугольному виду. Алгоритм, предложенный в предыдущем пункте, используется для последовательного зануления всех элементов первой строки (столбца) кроме одного, второй строки (столбца) – всех кроме двух и т.д. В итоге определитель преобразуется к треугольному виду. Величина такого определителя равна произведению элементов главной диогонали.

4). Вычисление с использованием теоремы Лапласа, согласно которой определитель 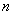- го порядка равен сумме произведений всех его миноров 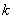-го порядка, стоящих в выделенных 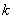строках (столбцах), на их алгебраические дополнения.

Обратная матрица

такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

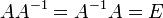
Минор

Минором 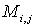элемента 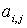матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-й строки и j-го столбца.

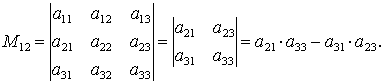
При выписывании определителя (n-1)-го порядка, в исходном определителе элементы находящиеся под линиями в расчет не принимаются.

Алгебраическое дополнение

Алгебраическим дополнением А_ij элемента а_ij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:

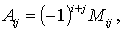
то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.