Решение уравнения номинальных размеров
А 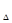 =
= 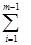 А
А 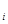
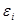
А 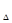 =170-12-12-23-23-27-65-8=0
=170-12-12-23-23-27-65-8=0
Проверим соответствие номинальных размеров требованиям ГОСТ 6636-69 ,устанавливаем, что размеры А8=27мм и А 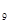 =65 в ряду Ra40 отсутствуют . За счет этих размеров можно достичь А
=65 в ряду Ra40 отсутствуют . За счет этих размеров можно достичь А 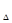 =0,приняв стандартные А
=0,приняв стандартные А 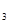 =25 мм и А
=25 мм и А 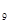 =67 мм
=67 мм
А 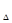 =170-12-12-23-23-25-67-8=0
=170-12-12-23-23-25-67-8=0
2.2. Расчет допусков составляющих звеньев размерной цепи
Определяем квалитет одинаковый для всех звеньев

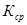 =
= 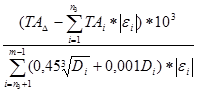

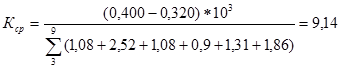
Согласно таблице 1 принимаем квалитет IT5, для которого К=7
Назначаем  допуски на все звенья ( кроме А
допуски на все звенья ( кроме А 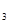 ), принимаемые в качестве специального звена по IT 5
), принимаемые в качестве специального звена по IT 5
ТА 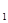 =0,008
=0,008
ТА 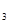 =ТА
=ТА 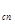
ТА 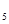 =0,008
=0,008
ТА 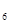 =0,16 (задан)
=0,16 (задан)
ТА 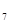 =0,006
=0,006
ТА  =0,009
=0,009
ТА 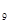 =0,013
=0,013
ТА 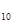 =0,16 (задан)
=0,16 (задан)
Определяем расчетный допуск на специальное звено
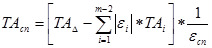
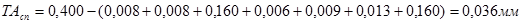
Ближайший стандартный допуск 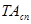 =0,025 мм , что соответствует 6 квалитету.
=0,025 мм , что соответствует 6 квалитету.
2.3.Определение предельных отклонений на все размеры
Назначаем на все размеры кроме специального, как на основные валы и отверстия , соответственно по h5 и H5 :
А  = 12
= 12 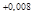
А  = А
= А 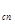
А 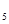 = 12
= 12 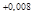
А 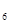 = 23
= 23 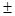 0,08
0,08
А 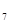 = 8
= 8 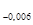
А  = 25
= 25 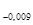
А 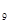 = 67
= 67 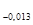
А 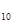 = 23
= 23 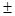 0,08
0,08
Определяем координату середины поля допуска специального звена
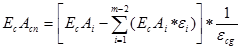
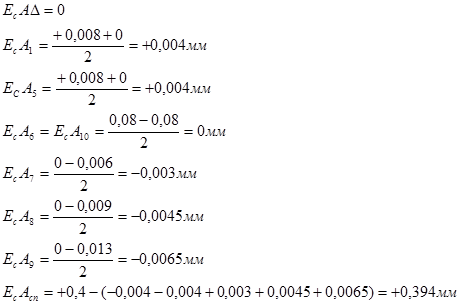
Определяем предельные отклонения специального звена
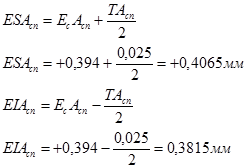
Таким образом А 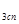
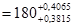
Подбираем ближайшее стандартное значение основного отклонения специального звена , которое по таблицам основных отклонений для диапазона 160-180 мм соответствует y = +380 мкм (расчетное основное отклонение ei = +3815 мкм).
А 
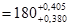 Е
Е 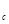 А
А 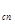 =+0,3925
=+0,3925
2.4. Проверяем правильность решения прямой задачи
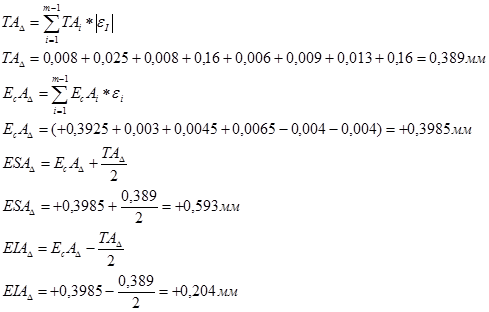
Таким образом 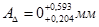
Анализируя выше проведенный расчет, делаем вывод о том, что метод полной взаимозаменяемости приемлем для нашей размерной цепи. Он обеспечивает размер замыкающего звена (зазора) с высокой точностью, но требование средней экономической точности не обеспечено.
Номинальные размеры звеньев размерной цепи с предельными отклонениями
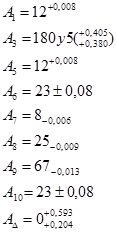
3. Решение прямой задачи методом неполной взаимозаменяемости (расчет вероятностным методом)
