Векторлардың аралас көбейтіндісі

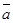Анықтама. , , векторларының аралас көбейтіндісі деп, және 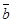векторларының векторлық көбейтіндісі мен векторының скаляр көбейтіндісін айтады.

Аралас көбейтінді не немесе түрінде жазылады. Аралас көбейтіндінің нәтижесі санға тең.

Аралас көбейтіндінің қасиеттері:

1. ;

2. ;

3. ;

4. Егер векторлар , , компланар болса, онда .

Теорема. базисінде , , векторлары берілсін, онда олардың аралас көбейтіндіні анықтауыш түрінде жазуға болады.

Аралас көбейтіндінің қолданылуы

1. Егер болса, онда , , -оң үштік; егер болса, онда , , - сол үштік құрайды.
2. , , векторлары компланар.
3. , .

Жазықтықтағы түзудің теңдеулері

Берілген нүктеден берілген векторға перпендикуляр өтетін түзудің теңдеуі

Түзудің бойында жатқан нүктесі және оған перпендикуляр векторы берілген. Түзудің бойынан кез келген нүктесін аламыз. Сонда болады. векторы түзудің бойында жатқандықтан болады. Сондықтан олардың скалярлық көбейтіндісі , яғни

(4.1)

Бұдан векторы түзуге перпендикуляр екендігі шығады. Түзуге перпендикуляр кез келген вектор түзудің нормалы немесе нормалдық векторы деп аталады.

Түзудің жалпы теңдеуі

(4.1) теңдеуінде жақшаларды ашып, деп белгілесек, түзудің жалпы теңдеуі шығады

(4.2)

Егер А=0 болса, онда түзу Ох өсіне параллель өтеді; егер В=0 болса, онда түзу Оу өсіне параллель өтеді; егер С=0 болса, онда түзу жүйенің бас нүктесі арқылы өтеді.

3. Түзудің бұрыштық коэффициент арқылы берілген теңдеуі. Егер болса, онда (4.2) теңдеуінен ( ):

(4.3)

4. Екі нүкте арқылы өтетін түзудің теңдеуі. Түзу және нүктелерінен өтсін. Түзудің бойынан кез келген нүктесін аламыз. Сонда бұл түзудің теңдеуі төмендегідей болады:

(4.4)

Түзудің кесінділік теңдеуі

Түзу және нүктелері арқылы өтсін. Сонда (4.4) формуласынан түзудің кесінділік теңдеуін аламыз:

(4.5)

Берілген нүктеден өтетін түзудің теңдеуі

(4.6)

7. Екі түзудің арасындағы бұрыш. және түзулерінің арасындағы бұрыштың формуласы:

(4.7)

Осыдан егер түзулер параллель болса, онда , ал түзулер перпендикуляр болса, онда болады. Түзулер және теңдеулерімен берілсе, онда , болғандықтан түзулердің арасындағы бұрыш осы екі нормальдің арасындағы бұрышқа тең:

(4.8)

Осыдан егер түзулер параллель болса, онда , ал перпендикуляр болса, онда болады.

8. Нүктеден түзуге дейінгі қашықтық. нүктесінен түзуіне дейінгі қашықтықтың формуласы:

(4.9)

2-мысал. нұктесінен тұзуіне дейінгі қашықтықты табу керек.

Әдебиеттер: 1 нег.[65-84], 11 қос. [156-167], [31-41].

Бақылау сұрақтар:

1. Скаляр көбейтіндінің векторлық көбейтіндіден айырмашылығы неде?

2. Аралас көбейтінді дегеніміз не?

3. Векторлық және аралас көбейтінділердің геометриялық мағынасын түсіндіріңіз.

4. Жазықтықтағы түзудің теңдеуіндегі бұрыштық коэффициенттің геометриялық мағынасы қандай?

5. Жазықтықтағы екі түзудің параллельдік және перпендикулярлық шарттарын айтыңыз.

Дәріс.

Дәріс тақырыбы:Кеңістіктегі жазықтық пен түзулер.

Дәрісжоспары:

§ Жазықтықтың теңдеулері.

§ Екіжазықтықтың арасындағы бұрыш.

§ Нүктеден түзуге дейінгі қашықтық.

§ Кеңістіктегі түзудің теңдеулері.

§ Түзу мен жазықтық.

§ Әдебиеттер.

§ Бақылау сұрақтары.