I.8. Дифференциальные соотношения термодинамики
Рассмотрим сопряжение по координатам. В этом случае сопряжения ранее была получена формула для k-того потенциала:
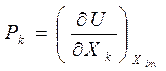
Запишем последнее уравнение для двух произвольно выбранных i-того и j-того потенциалов:
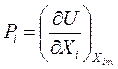 и
и 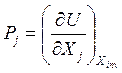
Продифференцируем первое выражение по j-той координате, а второе – по i-той:
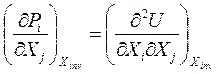 и
и 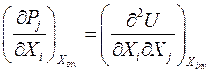
Как известно из математики, от изменения порядка дифференцирования результат не изменяется, поэтому правые части этих двух уравнений равны:
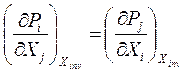 (62)
(62)
Действительное и обращённое соотношение:
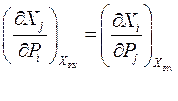 (63)
(63)
Уравнение (62) и (63) называются первым типом дифференциальных соотношений термодинамики.
Рассмотрим сопряжение по потенциалам. Без вывода, который аналогичен случаю сопряжения по координатам, сразу запишем прямое и обращенное соотношения:
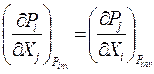 (64)
(64)
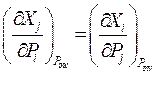 (65)
(65)
Уравнения (64),(65) называются вторым типом дифференциальных соотношений термодинамики.
Рассмотрим случай смешанного сопряжения. Без вывода запишем два прямых и два обращенных соотношения:
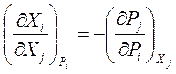 (66)
(66)
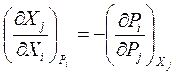 (67)
(67)
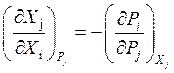 (68)
(68)
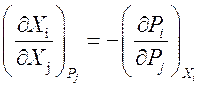 (69)
(69)
Уравнения (66), (67), (68), (69) называются третьим типом дифференциальных соотношений термодинамики.
В дифференциальных соотношениях нет частных производных, составленных из параметров одного и того же взаимодействия.
Так, производная 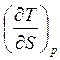 - не относится к дифференциальным соотношениям.
- не относится к дифференциальным соотношениям.
Если в одной частной производной термодинамический параметр находится в «знаменателе», то в другой частной производной (через знак равенства), соответствующий термодинамический параметр находится в «числителе». Для использования дифференциальных соотношений необходимо предварительно определить их тип.
Отличительные особенности дифференциальных соотношений:
1) 1-ый и 2-ой типы составлены из параметров разных классов (класс координат и класс потенциалов). Дифференциальные соотношения 3-его типа составлены из параметров одного класса;
2) в 1-ом типе дифференциальных соотношений инвариантными являются координаты, а во 2-ом – потенциалы.
3) В 3-ем типе индексы у инвариантных параметров берутся либо «по числителю», либо «по знаменателю».
Пример:
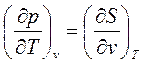 - 3-ий тип.
- 3-ий тип.
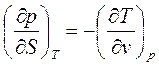 - 2-ой тип.
- 2-ой тип.
Для чего нужны дифференциальные соотношения термодинамики? Каждая частная производная в дифференциальных соотношениях термодинамики - это какое-то свойство системы (иногда без названия).
Например, 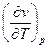 - это температурный коэффициент объёмного расширения системы (содержится в справочниках).
- это температурный коэффициент объёмного расширения системы (содержится в справочниках).
Пусть требуется опытным путем определить свойство системы, которое выражается частной производной 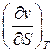 . Для проведения опытов запишем приближенное соотношение:
. Для проведения опытов запишем приближенное соотношение:
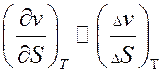
В этом соотношении V и T можно определить с помощью приборов, но энтропия прямыми приборными измерениями не определяется.
Воспользуемся 3-им типом дифференциальных соотношений, откуда
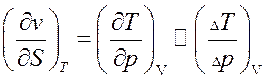
Получили приближенное соотношение, в котором все без исключения параметры (p, v, T) определяются прямыми измерениями.
Таким образом, дифференциальные соотношения термодинамики являются ее мощным средством, позволяющим заменить изучение одного свойства системы другим, более удобным для изучения.
Примеры:
1) 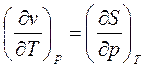 - 2-ой тип;
- 2-ой тип;
2) 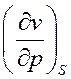 - не относится к дифференциальным соотношениям;
- не относится к дифференциальным соотношениям;
3) 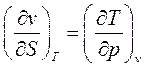 - 3-ий тип.
- 3-ий тип.
