Матрицаны сатылы түрге келтіру Гаусс алгоритмі.

А=( 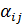) 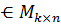(P) қандай да бір мат/а бол/н.

А мат/ң жол/на элементар түрлендірулер жасап сатылыSмат/н алу керек д.е.Егер А мат/сы нөл/к мат/а болса,онда S=А=0. Егер А≠0 болса,она келесі процедура/ды біртіндеп жасаймыз.

1.A мат\ң кем дегенде бір нөлдік емес бағаны бар. Нөлдік емес баған/ң ең кіші нөмірін 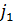деп белгілейік. 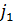ші бағанындағы нөлден өзге элементінің біреуін ,айталық 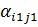элементін ерекше белгілеп алып оны бастаушы элемент деп атаймыз.

2.(a)түрлендірудің көмегімен астаушы элементі орналасқан 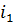ші жолын 1-ші жолмен алмастырып В мат/н аламыз.

B=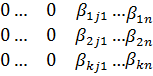

Бұл жерде .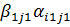

3.B мат/ң 2-ші жолынан 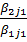коэф/ке көбейтілген 1-ші жолын, 3-ші жолынан

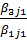коэф/ке көбейтілген 1-ші жолын, т.с.сk- ші жолынан 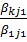коэф/ке көбейтілген 1-ші жолды алып тастасақ,

C=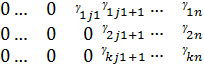

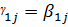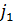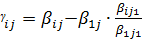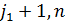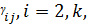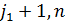мат/н аламыз. Бұл жерде , егер j= ,n болса : , егер i=2,k, j= болса. j= элементтерінен құралған мат/ны арқылы белгілейік. Егер D=0 болса онда S=C, керісінше D мат/на жоғарыда келтірілген процедураларын қайталаймыз, яғни С мат/ң 1-ші жолымен 1- 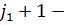ші бағандары алгоритмімізде одан әрі өзгермейді.

Гаусс алгоритмін бағандарға да жургізуге болады.

34.Векторлар жүйесіне қолданылатын элементар түрлендірулер. P-қандайда бір өріс, n-кез келген натурал сан ,ал 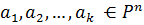болсын. 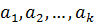векторлар жүйесіне жасалатын элементар түрлендірулер 3 типке бөінеді:

1. жүйенің кез келген екі век/ң орнын алмастыру;

2. жүйенің қандайда бір век/н P өрісінің кез келген нөлден өзгеше коэф/не көбйту;

3. жүйенің қандайда бір век/на басқа век/н кез келген P-ға тиісті коэф/ке көбейтіп алып,содан кейін қосу.

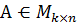(P) мат/ң 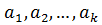жол/н 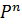арифметикалық кеңістігінің,ал 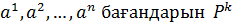арифметикалық кеңістігінің век/р жүйелері ретінде қарастыруға болады.Ендеше мат/ң жолдарына не бағандарына элементар түрлендірулерді жасауға болады.

35. Векторлар жүйесінің базасы және рангі.a_i1, a_i2,…a_inвекторлар жүйесі

a₁, a₂,…a_nвекторлар жүйесінің ішкі жүйесі болсын. Егер осы ішкі жүйе үшін келесі екі шарт орындалса, онда ол ішкі жүйені бастапқы жүйенің базасы деп атаймыз.

1. 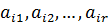сызықтық тәуелсіз

2. 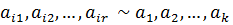(эквивалентті).

a₁, a₂,…a_nвекторлар жүйесінің кез келген базасының қуатын осы векторлар жүйесінің рангы деп атайды. 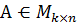k жолы мен n бағаны бар берілгенa₁, a₂,…a_n жолдар, векторлар жүйесінің 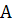матрицасының жолдар рангі деп a₁, a₂,…a_nвекторлар жүйесінің рангін айтады. А матрицасының бағандарының рангі деп {а ^-1 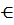Rⁿ, а ^-n 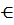Rⁿ} вектор жүйесінің рангі деп аталады.

36. Векторлар жүйесінің рангін табу әдісі.Анықтама: 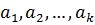векторлар жүйесінің кез келген базасындағы векторлар санын r 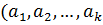) арқылы белгілейміз де, оны 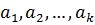жүйесінің рангі деп атаймыз.

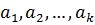жүйенің r 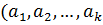) рангі жүйедегі тәуелсіз векторлардың максимал санына тең.

Век-ға қолданылатын сыз-тық амалдардың қасиеттері ж/е матрицаға қолданылатын сыз-тық амалдар бірдей. Гаусс алгоритмі векторлар жүйесінің сызықтық тәуелділігін зерттеу және оның рангі мен базасын табуға өте қолайлы тәсіл болып табылады.

37.Матрицаның рангі. Матрицаның рангін табу әдісі.Ан\ма: A=( 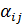), i=1,k; j=1,n мат/сы берілсін.

А= 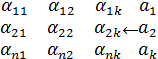қатар - 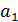… 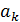⋲ 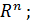баған- ⋲

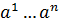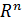
А мат/ң жолдар рангі депr( 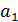… 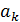) век/р жүйесінің рангін айтамыз

А мат/ң бағандар рангі деп r( 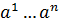) век/р жүйесінің рангін айтамыз

Мат/ң рангі туралы теорема: кез келген мат/ң жолдар ж/е бағандар рангі тең болады.

Матрицаның рангін табу әдісі.А мат/ң рангін табу үшін Гаусс алгоритмін қолданып, оны сатылы түрге келтіреміз S деп белгілейміз . Осы мат/ғы нөлдік емес жолдар саны А мат/ң рангі болады.

Век-ға қолданылатын сыз-тық амалдардың қасиеттері ж/е матрицаға қолданылатын сыз-тық амалдар бірдей.Сатылы мат-ның жолдар рангі бағандар рангіне тең ж/е ол бастауыш элементтер санына тең болады.А мат-ның рангін табу үшін оны сатылы түрге келтіреміз.