Полный факторный эксперимент
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ
имени академика С.П.Королева (СГАУ)
Факультет инженерно-технологический
Кафедра обработки металлов давлением
Отчет по лабораторной работе
по предмету:
«Методология научных исследований»
Выполнили студентки
группы 4122 М
Назинкин К.Э.
Калмантаев И.М.
Проверил преподаватель
Каргин В.Р.
Самара 2016
Понятие о планировании эксперимента
Планирование эксперимента — это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. Наиболее важными в областях науки и техники являются задачи, связанные с поиском оптимальных условий и построением математических моделей.
Поставленная задача решается на основе представления о кибернетической системе, которую называют «черным ящиком». Он представляет собой систему связей, недоступную для наблюдения, гак как о содержании, механизме процесса нам ничего не известно пли известно лишь частично. Известны только входы, переменные участвующие в процессе (факторы), и выходы — результат процесса (параметр оптимизации), обозначенный символом у.
Каждый фактор может принимать в опыте одно или несколько значений. Такие значения называются уровнями. Схема «черного ящика» позволяет строить математические уравнения, связывающие параметр оптимизации с факторами
у =f(x1, x2, ..., xk) .
Задача эксперимента состоит в том, чтобы определить численные значения коэффициентов этого уравнения. Обычно функцию, f(x1, x2, ..., xk) выбирают в виде степенного ряда. В частности, для двух факторов функция имеет вид полиномов первой степени У = b0 + b1x1 + b2х2 с неполным квадратным членом У = b0 + bxx1 + b2х2 + b12x1x2. Модель должна быть достаточно точной, т. е. близкой к фактической зависимости. Тогда считают, что она адекватна.
Полный факторный эксперимент
При планировании по схеме полного факторного эксперимента реализуются все возможные комбинации факторов на всех выбранных для исследования уровнях. Необходимое количество опытов N при полном факторном эксперименте определяется по формуле N = рк, где р — количество уровней, k — число факторов.
Если эксперименты проводятся на двух уровнях, то постановка опытов по такому плану называется полным факторным экспериментом типа 2к. Каждый фактор, участвующий в процессе, имеет определенный предел изменения своей величины. Совокупность всех значений, которые принимает фактор, называется областью определения фактора. Но в области определения надо найти локальную подобласть для планирования эксперимента, т. е. для каждого фактора необходимо указать тот интервал изменения параметров, в пределах которого проводятся исследования. Для этого на основании априорной информации устанавливаются ориентировочно значения факторов, комбинации которых дают наилучший результат. Этой комбинации значений факторов соответствует многомерная точка в факторном пространстве, которая принимается за исходную при построении плана эксперимента. Координаты этой точки называются основными уровнями факторов.
После того как основной уровень выбран, переходим к следующему шагу — выбору интервалов варьирования. Интервалом варьированияфактора называется некоторое число, прибавления которого к основному уровню дает верхний, а вычитание — нижний уровень фактора.
Поскольку факторы изучаемого процесса неоднородны и имеют различные единицы измерения, их следует привести к единой системе исчисления путем перехода от действительного значения факторов к кодированным по формуле
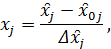
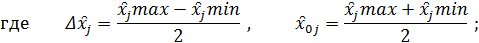
xj – кодированное значение фактора;
x̑j – натуральное значение фактора;
x̑0j - натуральное значение фактора на основном уровне;
j – номер фактора;
𝛥x̑j – интервал варьирования.
В безразмерной системе координат верхний уровень равен +1, нижний — соответственно —1, координаты основного уровня равны нулю. Для случая N— 22 условия проведения эксперимента записываются в виде таблицы, которую называют матрицей планирования эксперимента (табл. 1). Строки соответствуют различным опытам, столбцы — значениям факторов (единицы для упрощения записи опущены).
Таблица 1 - Матрица планирования 22
| N | 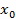 | 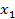 | 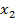 | P, N | 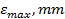 | 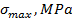 |
| +1 | +1 | +1 | 1.03· 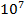 | 1,03 | ||
9,94· 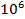 | 1,01 | |||||
| +1 | -1 | +1 | 6,49· 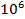 | 0,452 | ||
6,49· 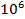 | 0,443 | |||||
| +1 | +1 | -1 | 9,51· 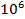 | 0,896 | ||
9,51· 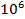 | 0,880 | |||||
| +1 | -1 | -1 | 6,27· 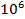 | 0,362 | ||
6,27· 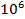 | 0,357 |
Р – усилие
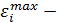 интенсивность деформации
интенсивность деформации
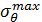 – максимальное окружное напряжение
– максимальное окружное напряжение
Таблица 2 – Данные эксперимента
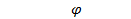 Уровни Уровни | 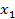 | 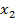 |
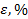 | 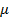 | |
| +1 | 0,3 | |
| 0,1 | ||
| -1 | 0,2 | |
| Интервал | 0,1 |
Построение матриц планирования основано на правиле чередования знаков. В первом столбце они меняются поочередно, во втором чередуются через два, в третьем — через четыре и т. д. по степеням двойки. По результатам эксперимента определяются коэффициенты математической модели
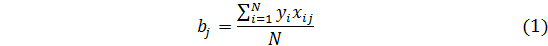
Чтобы провести процедуру вычисления коэффициента b0 в соответствии с формулой (1), в матрицу планирования введен столбец фиктивной переменной х0, которая во всех опытах принимает значение +1.
Определение коэффициентов математической модели:
1. Усилия:
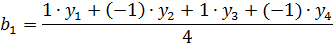
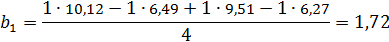
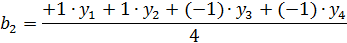
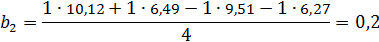
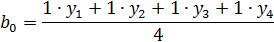
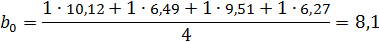
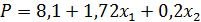
На усилие влияет степень деформации. При увеличении коэффициента трения усилие возрастает.
2. Интенсивность деформации:
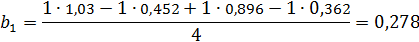
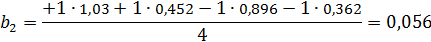
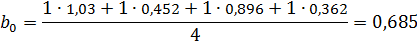
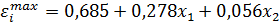
На интенсивность деформации влияет степень деформации
3. Максимальное окружное напряжение:
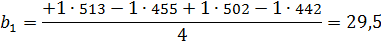
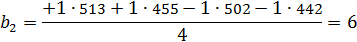
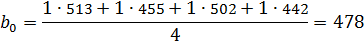
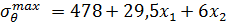
На максимальное окружное напряжение влияет трение.
