Количество информации при измерении. Избыточность

Количество информации только тогда равно энтропии, когда неопределенность ситуации снимается полностью.
В общем случае нужно считать, что количество информации есть уменьшение энтропии вследствие опыта или какого-либо другого акта познания.
Если неопределенность снимается полностью, то информация равна энтропии, т.е.

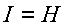
(2)

В случае неполного разрешения имеет место частичная информация, являющаяся разностью между начальной и конечной энтропией

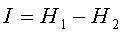
(3)

Если рассматривается измерение, то погрешность оказывает дезинформационное действие. Энтропию H2 можно определить с помощью выражения для энтропии случайных величин с непрерывным распределением:

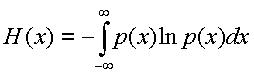
(4)

Замена логарифма с основанием два на натуральный произведена для удобства логарифмирования распределений p(x), которые в большинстве случаев являются экспоненциальными.
Абсолютная избыточность информации Дабс представляет собой разность между максимально возможным количеством информации и энтропией:

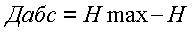
(5)

Иными словами, если мы можем получать количество информации большее, чем неопределенность объекта, то мы создаём искусственно ситуацию с наличием избыточной информации.
Относительная избыточность равна

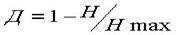
(6)

Пример №1
Пусть полная шкала отсчётного устройства содержит 1000 элементарных единиц (делений, градаций), а погрешность средства измерений (без учёта погрешности отсчёта) составляет ±1%. Найти относительную избыточность, которая может возникнуть при неправильном проектировании средства измерений.
Рассмотрим количество информации при снятии показаний с отсчётного устройства. Наличие 1000 градаций предусматривает 1000 возможных значений, которые могут быть отсчитаны. Таким образом, максимальное количество информации равно

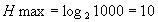
Неопределенность измеряемой величины до отчетного устройства, вследствие наличия погрешности, составляет ±1%, т.е. полная ширина неопределённости h составляет 2%.
Таким образом количество различных градаций К соответствует количеству непересекающихся полос шириной 2%, а именно

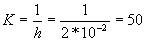
Тогда количество информации до отсчётного устройства составляет

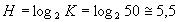
Т.к. количество информации, снимаемое с отсчётного устройства превышает Н, налицо избыточность. Значение относительной избыточности равно:

Д=1-0.55=0.45.

2.24 Энтропийный интервал неопределённости

Соотношения I=lnN и N=( 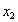- 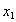)/d справедлевы при любом распределении погрешностей, если только интервал неопределённости d будет найден через энтропию. Поэтому было предложено [Новицкий П.В., Зограф Н.А. Оценка погрешностей результатов измерений. - Л.: Энергоатомиздат. Ленингр. отделение, 1991.] называть число N числом эквивалентных делений, различимых в диапазоне 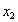- 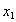при данном распределении погрешности p(x), а d- эквивалентным в энтропийном смысле делением. Нужно отметить, что причиной появления избыточности при отсчёте является то, что деление, нанесённое на шкале, оказывается намного меньше эквивалентного деления.
При использовании информационного подхода d называют энтропийным интервалом неопределённости результата измерения.
Энтропийный интервал неопределённости (13), (14) был рассчитан для равномерного распределения погрешности.
Рассмотрим пример расчёта для нормального распределения погрешности с плотностью вероятности

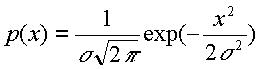
(15)

Тогда

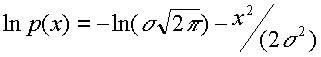
(16)

Отсюда энтропия погрешности

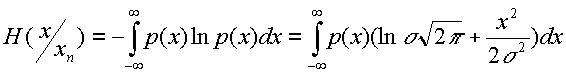
(17)

Представим выражение (17) в виде

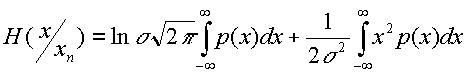
(18)

Учитывая, что

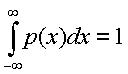
и по определению дисперсии

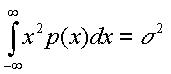
получаем

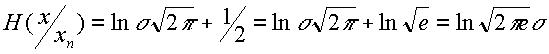
(19)

Таким образом, интервал неопределённости d результата измерения, найденный через энтропию в соответствии с теорией информации, равен 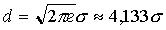, а число различимых градаций результата измерения при равномерном распределении вероятности различных значений измеряемой величины

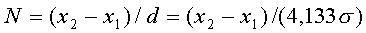
(20)

Подобным же образом энтропийный интервал неопределённости результата измерения может быть однозначно найден для любого выраженного аналитически закона распределения погрешности. Например, при распределении погрешности по треугольному закону Симпсона

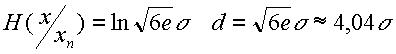
(21)