Ograve; ò x

dx

ò ò

÷

ç

è x ø

y2 x2

ò у dy = ò x

+ ò x dx ,

= ln 2

x + + c ,

2

y2 - x2

2

= ln

x + c .

Мы получили соотношение между х, у и произвольной

постоянной с, которое называется общим интегралом.

в) Разрешим уравнение относительно производной у :

у¢ = - 4х - 3у

2 у - 3х

или

у¢ = 4х - 3у . (1)

3х - 2 у

Правая часть этого уравнения

f (x, у) = 4x - 3y

3x - 2 y

является однородной функцией нулевого порядка относительно своих аргументов, так как удовлетворяет следующему условию:

В самом деле,

f (tx,ty) =

f (x, y) .

f (tx,ty) = 4(tx)-3(ty)

3(tx) - 2(ty)

= t (4x -3y) t (3x - 2 y)

= 4x -3y =

3x - 2 y

f (x, y) .

Отсюда следует, что уравнение (1) является однородным. Од-

нородное уравнение решают подстановкой Найдем у¢ и подставим в уравнение (1):

y¢ = u¢ × x + u ,

u = y x

или

y = u × x .

u¢ × x + u = 4x - 3ux ,

3x - 2ux

u¢ × x = 4-3u - u ,

3 - 2u

u¢ × x + u = x(4 - 3u) ,

x(3 - 2u)

u¢ × x = 4-3u -u (3-2u) ,

3 - 2u

u¢ × x = 2u -6u +4 .

3 - 2u

Получившееся уравнение оказывается уравнением с разделяю- щимися переменными. Разделяем переменные:

du 2u 2 -6u +4

x = ,

(3 - 2u) du

= dx ,

dx 3 - 2u

2u2 - 6u + 4 x

после чего интегрируем:

ò

3 - 2u

dx

du = ò ,

2u2 - 6u + 4 x

1

- 2 ò

4u - 6 du

2u2 - 6u + 4

= - 1 ò

d(2u -6u +4) =

2u2 - 6u + 4

= - 1 ln 2u2 2

dx

- 6u + 4 + c1 , ò x

= ln

x + c1 .

Получаем общий интеграл:

- 1 ln 2u2 - 6u + 4 = ln 2

x + ln c , где

ln c = c2

– c1 .

После потенцирования общий интеграл примет вид

2u2 - 6u + 4 =

1 .

c2 x2

Вернемся к старой функции у, подставив вместо u у :

х

æ у ö2 у

1

2 ç ÷ - 6

+ 4 =

è х ø х

с2 х2

или

2 у2 - 6ху + 4х2 = 1 .

с2

с) В данное уравнение неизвестная функция у и ее произ-

водная у¢ входят в первой степени. Отсюда следует вывод: уравнение является линейным. Будем искать решение линейно- го уравнения в виде произведения двух пока неизвестных

функций u (x) и v (x), т. е.

у = u × v . Найдем производную

у¢ = u¢ × v + u × v¢

и подставим в уравнение (2):

x (u¢ × v + u × v¢) + 2u × v = x2 ,

x × u¢ × v + x × u × v¢ + 2u × v = x2 ,

x × u¢ × v + ( x × u × v¢ + 2u × v) = x2 ,

x × u¢ × v + u ( x × v¢ + 2v) = x2 .

Для нахождения функции v (x) положим:

x × v¢ + 2v = 0 .

Найдем частное решение (для этого положим с = 0) этого

уравнения с разделяющимися переменными:

x dv = -2v ,

dv = -2 dx ,

dx v x

dv dx 1

ò v = -2 ò x ,

ln v = -2 ln x ,

v = .

x2

Для нахождения другой функции u (x) у нас получается

уравнение:

x × u¢ × v = x2 ,

x × u¢ 1

x2

= x2 ,

u¢ = x3 ,

du = x3 , dx

du = x3dx , ò du = ò x3dx ,

u = x

+ c .

Общее решение данного уравнения (2) будет иметь вид

æ x4

ö 1 x2 c

y = u × v = ç + c ÷ = + .

x

ç ÷ 2

è ø

4 x2

Задача 2.Найти частное решение дифференциального уравнения

2х × у¢ - у =

3х2

,

у

удовлетворяющее начальному условию

у (1) = 2 .

Решение:Уравнение Бернулли имеет вид

у¢ + р( х) у = q( x) yn ,

n ¹ 0 ,

n ¹ 1.

Данное уравнение можно записать в виде

у¢ - у

2х

= 3х

2х

у-1 ,

поэтому делаем вывод: данное уравнение является уравнением

Бернулли. Его можно решать тем же методом, что и линейное

уравнение. Будем искать общее решение в виде

у¢ = u¢ × v + u × v¢ ,

у = u × v :

u¢ × v + u × v¢ - u × v =

2x

æ ö

3x ,

2u × v

3

u¢ × v + u ç v¢ -

v ÷ = x ,

è 2x ø

2u × v

v¢ - v

= 0 ,

dv = dx , ò dv = 1 ò dx ,

2x v 2x

v 2 x

ln v = 1 ln x ,

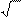v = x

– одну функцию нашли.

u¢ ×

x = 3x ,

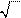
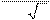2u × x

du = 3 ,

dx 2u

2u du = 3dx , ò 2u du = ò 3dx ,

u2 = 3x + c

или

u = 3x + c .

Общее решение уравнения примет вид

y = u × v =

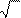3x + c × x =

3x2 + cx .

Чтобы найти частное решение уравнения, нужно найти значение константы с. Для ее нахождения подставим в общее решение х = 1 и у = 2:

2 = 3×1 + с ×1 =

3 + с ,

4 = 3 + с , с = 1.

Подставив в общее решение значение с = 1, получаем ча-

стное решение у =

3х2 + х .

Задача 3.Найти общее решение дифференциального уравнения второго порядка

Решение:

у¢ + 1

х

у¢ = х2 .

В данном уравнении второго порядка отсутствует в явном

виде сама функция у. Это уравнение допускает понижение по-

рядка, для чего надо сделать замену уравнение примет вид

у¢ = z (x) . Тогда

у¢ = z¢ и

z¢ + 1 z = х2 . (3)

х

Уравнение (3) оказывается линейным уравнением первого

порядка относительно функции z (x) и решается следующим об- разом:

z = u × v ,

u¢ × v + u × v¢ + u × v = x2 ,

z¢ = u¢ × v + u × v¢ ,

u¢ × v + u ç v¢ + v ÷ = x ,

v¢ + v = 0 ,

æ ö

x è x ø 2

dv = - dx , ò dv = -ò dx ,

x

ln v = - ln x ,

v x v x

v = 1 ;

x

u¢ 1 = x 2 ,

x

du = x3dx , ò du = ò x3dx ,

u = x

4

+ c1 .

Общее решение уравнения (3) примет вид

1 æ x4

z = u× v = ç

ö x3

+ c ÷ =

x

+ c1 .

è

ø

x ç 4 1 ÷

В начале решения была сделана замена

y¢ = z . Следовательно,

y¢ = x

+ c1 .

4 x

Это уравнение с разделяющимися переменными. Решая его, по-

лучаем

æ x3 dy = ç

c ö

+ 1 ÷ dx ,

x

ç ÷

è ø

æ 3 ö

ç 4

ò dy = ò ç x

è

+ c1 ÷ dx ,

x

÷

ø

x4

y = + c1 ln x + c2 - общее решение данного уравнения.

Задача 4.Найти частное решение уравнения

у¢ + 4 у¢ = х2 + 5х ,

удовлетворяющее начальным условиям

у(0) = 1,

у¢(0) = 0 .

Решение:

Данное уравнение является линейным дифференциальным

уравнением второго порядка с постоянными коэффициентами с

правой частью специального вида

f (x) = Pn (x) , где

Pn (x) -

многочлен степени n. Общее решение такого уравнения скла- дывается из общего решения однородного уравнения (правая часть равна нулю) и какого-либо частного решения неоднород- ного уравнения.

Решим сначала однородное уравнение

у¢ + 4 у¢ = 0 .

Составляем характеристическое уравнение

k 2 + 4k = 0 ,

корнями которого будут

k1 = 0

и k2 = -4 .

Соответственно этим корням находим частные решения

y1 = e

k1x

= eox = 1 и

y2 = e

k 2 x

= e-4 x

и общее решение, которое представляет собой линейную ком- бинацию найденных частных решений:

y = c y

+ c y

= c ×1 + c e-4 x .

o.o

1 1 2 2 1 2

Теперь надо найти частное решение неоднородного уравнения.

Пользуясь таблицей, мы будем искать частное решение неоднородного уравнения в виде

уч.н

= ( Ах2 + Вх + С) х ,

так как правая часть f (x) уравнения представляет собой много- член второй степени, а число 0 является корнем характеристи- ческого уравнения с кратностью s = 1.

Нам остается найти неизвестные пока коэффициенты А, В, С. Для этого найдем первую и вторую производные от уч.н и подставим найденные выражения в данное неоднородное урав- нение:

уч.н

= Ах3 + Вх2 + Сх ,

у¢ = 3Ах2 + 2Вх + С ,

у¢ = 6Ах + 2В ,

6 Ах + 2В + 4(3Ах2 + 2Вх + С) = х2 + 5х ,

12Ах2 + (6 А + 8В)х + (2В + 4С ) = х2 + 5х .

Из полученного равенства двух многочленов следует ра- венство коэффициентов при одинаковых степенях х в левой и правой частях:

ïì12А = 1;

í6А + 8В = 5;

ïî2В + 4С = 0 .

Решением системы являются:

А = 1 ,

В = 9 ,

16

С = - 9 .

32

Значит, частное решение имеет вид

уч.н

= 1 х3 + 9

12 16

х2 -

9 х ,

32

а общее решение есть

уо.н

= уо.о

+ уч.н

= с1

+ с е- 4 х + 1

12

х3 + 9

16

х2 -

9 х .

32

Найдем значения постоянных с1 и с2. Для этого сначала продифференцируем полученное общее решение:

у¢ = -4с е- 4 х + 1 х2 + 9 х - 9 .

2 4 8 32

Теперь подставим

х = 0

в выражения для у и у¢:

у (0) = с1 + с2 = 1,

у¢ (0) = -4с2 -

Решим систему:

= 0 .

ïìс1 + с2 = 1,

í- 4с

- 9 = 0 .

Найденные

ïî

с = 137

1 128

и с2

= - 9

подставим в общее ре-

137 - 9 е- 4 х + 1 х3 + 9   х2 - 128 128   12 16

шение и получим частное решение:

у = х .

Задача 5.Найти общее решение системы линейных диф- ференциальных уравнений с постоянными коэффициентами пу- тем сведения ее к одному уравнению второго порядка:

ì dx

ï dt

í dy

ï

î dt

= 4x + 2 y,

= - x + y .

Решение:

Продифференцируем обе части первого уравнения по пе-

ременной t:

ö

æ dx ¢

ç ÷ = (4x + 2 y)¢

или

x¢ = 4x¢ + 2 y¢ .

è dt ø

Чтобы получить дифференциальное уравнение второго порядка относительно функции х (t), подставим вместо у¢ ее вы- ражение из второго уравнения системы:

x¢ = 4x¢ + 2(- х + y)

или

x¢ = 4x¢ - 2 х + 2 y . (5)

Из первого уравнения системы найдем 2у:

2 у = х¢ - 4х

и подставим в уравнение (5):

x¢ = 4x¢ - 2 х + х¢ - 4х

или

x¢ - 5х¢ + 6х = 0 .

Полученное уравнение является линейным однородным

уравнением с постоянными коэффициентами. Находим корни соответствующего характеристического уравнения

2t

3t

k 2 - 5k + 6 = 0 ,

k1 = 2 ,

k2 = 3 . Тогда

x1 = e

и x2 = e ,

а x = c1

·x1

+ c2

·x2

= c1

·e2t + c2

· e3t .

Одна из неизвестных функций х (t) найдена. Для нахожде-

ния второй функции у (t) воспользуемся соотношением, полу-

ченным ранее:

у = х¢-4х .

Тогда

x¢ = 2c1

·e2t + 3c

·e3t ,

x¢ - 4х = 2c1

·e2t + 3c2

·e3t - 4c

·e2t - 4c

· e3t = -2c

·e2t - c

·e3t ,

y = -c

·e2t - 1 c

·

e3t .

1 2 2

Общее решение данной системы имеет вид

ìx = c

·e2t + c

· e3t ,

ï 1

í 2t

1 3t

ïî y = -c1 × e

- c2 × e .