I. Метод Гауса та його модифікації.

Запишемо систему (1) у розгорнутому вигляді:

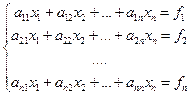(2)

Метод Гаусса розв’язання системи (2) полягає у послідовному вилученні невідомих 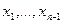з цієї системи. Вважаємо, що a₁₁ ¹0, поділимо 1-ше р-ня на a₁₁:

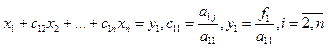(3)

Розглянемо тепер рівняння системи (2), що залишилися

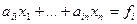; i= 2,n . (4)

Помножимо (3) на - 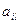та додамо одержане рівняння до і-го рівняння системи (4), i=2,n.

У результаті одержимо наступну систему рівнянь:

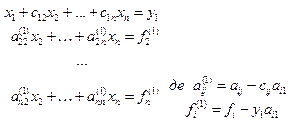. Ми отримаємо трикутну матрицю, де на k-му кроці перетворення коефіцієнти визначаються формулою 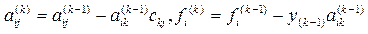. Виконується, коли ведучий елемент ¹0. Якщо ведучий елемент =0, тоді у рядку нижче шукають ненульовий елемент і переставляють місцями рядки.

Виконані нами дії еквівалентні множенню обох частин початкової системи зліва на елементарну трикутну матрицю вигляду:

Не важко побачити, що одне перетворення методу Гауса еквівалентне множенню системи на L₁^-1: 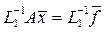. Нехай у нас уже оброблено і-1 стовпчик початкової матриці. Тоді матриця L_і^-1 матиме вигляд: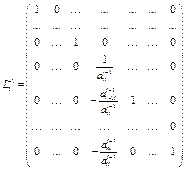

Продовжуючи таким чином до останнього рівняння одержимо систему з трикутною верхньою матрицею , де U= A – верхня трикутна матриця. Тобто отримаємо: .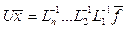

Метод Гауса вимагає n³/3+О(n²) операцій додавання і віднімання і стільки ж операцій множення і ділення.

Ітераційне уточнення одержаного розв’язку:

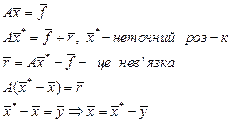Уточнення не треба, якщо y має порядок похибки округлення.

II Метод віддзеркалення.

Цей метод базується на розкладі матриці СЛАР (сис-ми лін. алгебраїчних рівнянь) на добуток ортогональної і верхньої трикутної матриці. A=QR , де Q – ортогональна матриця, яка є добутком елементарних ортогональних матриць, так званих матриць віддзеркалення або перетворень Хаусхолдера. Цей метод вимагає вдвічі більше операцій, ніж метод Гауса.

III Для специфічних матриць:

1) Якщо матриця симетрична, то метод квадратного кореня використовує в 2 рази менше часу, ніж метод Гауса. A - симетрична, A=LL^T, L - нижня, L^T- верхня трикутна матриця.

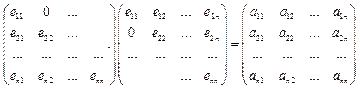
Звідси 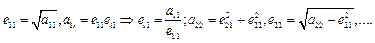, і взагалі, 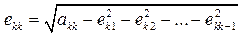, 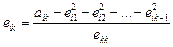. Цей метод має недоліки, якщо в системі присутні дійсні коефіцієнти (при розрахунках на ПЕОМ).

2) Матриця A (система рівнянь з цією матрицею) має тридіагональний вигляд:

В цьому випадку для роз-ку задачі використовується метод прогонки, який вимагає порядку 8 n операцій. Якщо здійснити розщеплення, то можна очікувати, що вони дводіагональні, отже існує зв’язок 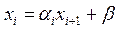, тоді 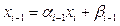. Цей вираз підставимо в і-те рівняння. Для визначення покрокових a і b ми маємо перше рівняння 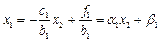. Метод визначення a і b називається прямим ходом прогонки. Якщо відоме останнє x_n, то зворотнім ходом можна визначити всі x_n-1,..,x₁. А x_n ми оберемо з останнього рівняння 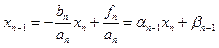. Метод прогонки потребує O(n).

Ітераційні методи

Багато практично важливих задач зводяться до роз-ня СЛАР дуже великої розмірності, матриці яких не є щільно заповненими (містять багато нульових елементів). У цьому випадку вигідно застосовувати ітераційні методи. Розглянемо систему . Ітераційні методи складаються з перетворень цієї системи до еквівалентної: 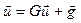та організації обчислювального процесу 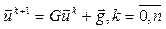при заданому початковому наближенні 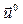. За таких умов процес 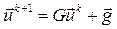буде збігатися до дійсного розв’язку системи. Розглянемо послідовність , 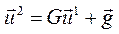і т.д., де 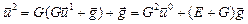,..., та зрозуміло У нас для оптимального розв’язку послідовність 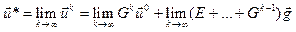повинна бути скінченою. Для цього необхідно , а тоді 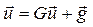приймає вигляд . Існує декілька підходів для отримання цього з 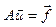. Розглянемо ці підходи:

1. Метод Якобі. Вважаємо, що a₁₁¹0, тоді , ..., . (*)

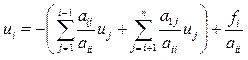Визначимо ітерації формулами: 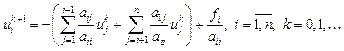Якщо задати вектор , то можна сподіватися, що при 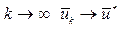. Цей метод носить назву методу Якобі. Як і для багатьох ітераційних методів для цього методу існує 2 критерії припинення процесу: 1) кількість ітерацій досягає верхньої критичної межі; 2) виконується умова досягнення потрібної точності. Такою умовою може бути: .

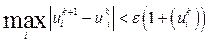3. Методи інтерполювання. Множники Лагранжа та Ерміта. Сплайни.

Задача наближення функцій виникає при розв’язанні багатьох задач ( обробка експериментальних даних, чисельне диференціювання та інтегрування функцій, розв’язання диференціальних та інтегральних рівнянь).

Дуже зручною у використанні на практиці функцією є многочлен. Щоб задати многочлен, треба задати тільки скінчену кількість його коефіцієнтів. Значення многочлена просто обчислюються, його легко продиференціювати, проінтегрувати і т.д. Тому алгебраїчні многочлени знайшли широке застосування для наближення (апроксимації) функцій.

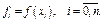Постановка задачі інтерполяції. Нехай відомі значення деякої функції у різних точках які позначимо Виникає задача поновлення

( наближеного) функції у довільній точці .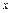

Іноді відомо, що наближену функцію доцільно шукати у вигляді

де вигляд функції 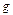відомий, а параметри треба визначити.

Коли параметри визначаються з умови збігу 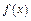і наближеної функції 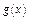у точках тобто то такий спосіб наближення називається інтерполяцією. Точки 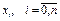називаються вузлами інтерполяції.

Серед способів інтерполяції найбільш поширеним є випадок лінійної інтерполяції .

де 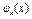- деякі відомі функції. Значення коефіцієнтів визначаються з умови збігу з вихідною функцією у вузлах інтерполяції

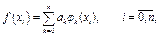(1)

тобто з системи n +1 лінійних рівнянь з n+1 невідомими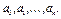

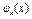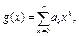Достатня умова існування єдиного роз-ку сис-ми для довільного набору вузлів є вимоги, щоб ф-ція була ф-цією Чебешова: . Тоді отримаємо (2)

тобто інтерполяція здійснюється многочленом, який називається інтерполяційним.

Теорема. Якщо вузли интерполяції різні, то існує єдиний інтерполяційний многочлен n-го ступеню.

В загальному вигляді 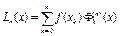, (3)

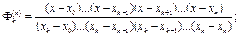(4)

Інтерполяційний многочлен, представлений у вигляді (3), називається інтерполяційним многочленом Лагранжа, а функції (коефіцієнти) (4) - Лагранжевими коефіцієнтами. Існують також інші форми запису інтерполяційного многчлену, але за наведеною теоремою інтерполяційний многочлен n-го степеня – єдиний.

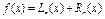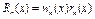Завжди можна записати рівність , де - залишковий член, тобто похибка інтерполювання. шукають у вигляді , де 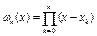, а r_n(x) - деяка функція, значення якої у вузлах інтерполяції x_i можна задавати які завгодно, оскільки 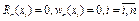. Оцінка похибки інтерполяції в поточній точці xÎ [a,b] має вигляд 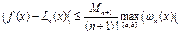, де const M дорівнює .

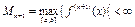Лінійна інтерполяція.

Інтерполяція за формулою при n=1, тобто за допомогою лінійної функції 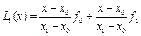, називається лінійною. Якщо ввести позначення 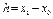, то формула лінійної інтерполяції запишеться у вигляді , де q називається фазою інтерполяції, яка змінюється від 0 до 1, коли x пробігає значення від x₀ до x₁.

Многочлени Чебишева.

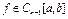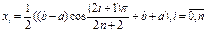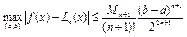Для того, щоб максимальна похибка інтерполяції функції f на відрізку [a,b] ( ) була мінімальною, в якості вузлів інтерполяції беруть корені многочлена Чебишева T_n+1(x): . Ці точки є оптимальними вузлами оцінки похибки інтерполяції на відрізку [a,b]. Оцінка похибки має вигляд , де .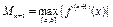

Інтерполяція з рівновіддаленими вузлами.

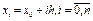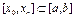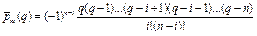Якщо відрізок [a,b] великий і необхідна висока точність апроксимації функції, то часто користуються таблицею значень функції у вузлах, що розбивають відрізок з постійним кроком, число їх може бути достатньо великим. Нехай - вузли інтерполяції, h>0 - крок, причому . Позначимо , тоді інтерполяційний многочлен буде мати вигляд , де . 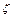Залишковий член (похибка інтерполяції) має вигляд , де - n+1 похідна по x, - деяка проміжна точка, .

Інтерполювання з кратними вузлами.

Побудувати многочлен 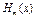степеня m такий, що 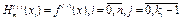. Многочлен 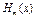називається інтерполяційним многочленом Ерміта.

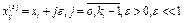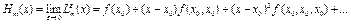
Нехай при таких умовах ; – многочлен Ерміта.

Сплайни.

Перевагою сплайнів над звичайною інтерполяцією є, по-перше, їх збіжність, і, по-друге, стійкість процесу обчислень.

Інтерполювання сплайном полягає в наступному: область визначення функції D(u) ділять на частини D_і, , які не перетинаються між собою і для яких 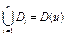, в кожній частині ф-ція визначається як поліном і називається сплайн-функцією.

На відрізку [a,b] визначимо сітку 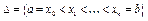, по вузлах якої задане значення функції. Назвемо сплайном 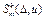функцію, яка є поліномом степеня m на кожному проміжку з сіткою ∆, в вузлах х_і приймає значення і має в цих вузлах неперервні похідні до порядку k включно. m – це порядок сплайну, m-k – це дефект сплайну. На практиці найбільш широке розповсюдження отримали сплайни третього степеня. Ці сплайни називаються кубічними і позначаються S₃(x).

Озн. Кубічним сплайном називається функція, яка має такі властивості:

а) на кожному сегменті 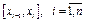функція 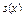є поліномом третього степені;

б) функція 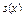, а також її перша і друга похідні неперервні на ;

в) ;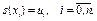

г) 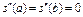.8

Озн. Умова в) називається умовою інтерполювання.

Озн. Сплайни, які задовольняють умову г) називаються природніми.

Озн. Величина 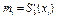називається нахилом сплайну в точці (вузлі) x_i.

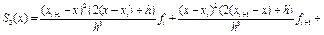
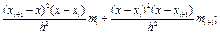
Отже, щоб задати кубічний сплайн S₃(x) на всьому відрізку [a,b], необхідно задати в N+1 узлах x_i його значення f_i та нахили m_i, i=0,...,N. Нахили можна задати, наприклад, так: , , причому , , h=(b-a)/N.

4. Методи чисельного інтегрування.

Розглянемо методи наближеного знаходження визначених інтегралів 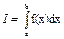, що засновані на заміні інтегралу кінцевою сумою , де - числові коефіцієнти, 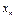- точки відрізку [a,b], k = 0,1,..,n. Для знаходження таких інтегралів використовуються квадратурні формули інтерполяційного типу (*).

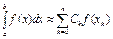- квадратурна сума, 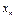- вузли квадратурної формули, - коефіцієнти квадратурної формули. Різниця - похибка квадратурної формули, залежить як від розташування вузлів, так і від вибору коефіцієнтів.

Нехай має місце (*), а коефіцієнт будемо шукати з умови точності цієї формули для поліномів вищого степеня. Розглянуті нами формули називаються формулами з фіксованими вузлами інтегрування. Якщо ж вузли інтегрування заздалегідь не визначати, то можна намагатися одержати квадратурну формулу точну для поліномів 2n+1 степеня. Такі формули, де зафіксовані і вагові коефіцієнти і вузли називаються формулами найвищого алгебраїчного степеня точності або формулами типу Гауса. Але щоб одержати всі невідомі, треба розв’язувати нелінійну систему рівнянь або систему нелінійних рівнянь.

Теорема чисельного інтегрування:

Нехай 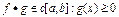на [a,b]. Тоді таке, що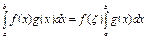

Розглянемо такі квадратурні формули:

a) формула прямокутників с залишковим членом

,

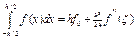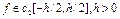
б) формула трапецій с залишковим членом

,

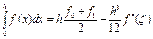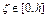
в) Формула Сімпсона ( формула парабол )

,

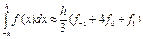Вище розглянуті квадратурні формули - канонічні. Можна побудувати ускладнені формули на [a,b] : відрізок [a,b] ділимо на N частин, до кожної застосували якусь канонічну квадратурну формулу і сумують результати. Так виведемо ускладнену квадратурну формулу прямокутників:

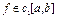часткові відрізки : ,

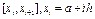i=0,1,..,N-1, , h=(b-a)/N

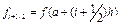- значення f

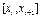в середині відрізку , при цьому

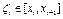, - деяка точка

скадаючи отримаємо ускладнену квадратурну формулу.

, - точка [a,b]

ускладнена квадратурна формула з залишковим членом.

5. Чисельні методи розв’язання задачі Коші.

Розглянемо диференційне рівняння першого порядку:

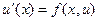(1).

Задача Коші полягає в наступному: знайти розв’язок u(x) рівняння 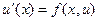, що задовольняє початкову умову 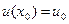(2).Функція u(x) може бути як скалярною, так і векторною.

Загальний вигляд задачі Коші для n-го порядку звичайних диференційних рівнянь має вигляд:

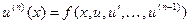(3).Для такої задачі початкові умови записуються так: 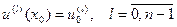(4). Вони дозволяють виділити з мн-ни роз-ків єдиний роз-к:

.

Всі методи розв’язання задачі Коші діляться на 2 типа: 1) точні; 2) наближені. В свою чергу наближені поділяються на 2 типи: 1) аналітичні; 2) чисельні.

В аналітичних методах роз-к будується як послідовність функцій . Перевага цього роз-ку в тому, що він у вигляді функції. До аналітичних методів належать такі методи як метод послідовних наближень та метод степеневих рядів.

Чисельні методи дають роз-к лише на деякій мн-ні точок, тобто у вигляді таблиці. Ці значення теж будуть наближеними. Чисельні методи бувають однокрокові та багатокроккові. В однокрокових методах для знаходження роз-ку в якійсь точці використовується лише інформація в попередній точці. В бгатокрокових методах для знаходження роз-ку в якійсь точці використовується інформація в декількох попередніх точках.

Розглянемо деякі чисельні методи роз-ня задачі Коші.

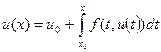. Якщо використати це рівняння то можемо написати: 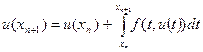(5). Отже, якщо у нас було відоме 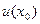, то ми зможемо знайти 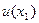. Введемо сітку: . Тоді роз-к задачі (1), (2) на цій сітці можна одержати з (5) шляхом заміни інтеграла деякою квадратурною формулою:

Метод Ейлера

Замінимо інтеграл квадратурною формулою лівих прямокутників. Одержимо 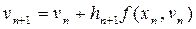(6) – формула Ейлера.