Сызықтық оператордың ядросы мен образы
Айталық, 
 L(V
L(V  ) берілсін.
) берілсін.
Анықтама. V  кеңістігінің,
кеңістігінің,  сызықтық операторының нәтижесінде нольдік векторға көшетін векторларының жиынын
сызықтық операторының нәтижесінде нольдік векторға көшетін векторларының жиынын  сызықтық операторының ядросы деп атайды және ker
сызықтық операторының ядросы деп атайды және ker  деп белгілейді. ( kernel – ядро). Сонда,
деп белгілейді. ( kernel – ядро). Сонда,
ker  =
= 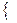 х
х  V
V  |
|  (х) = 0
(х) = 0 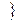 .
.
Анықтамадан ker 
 V
V  болатыны түсінікті.
болатыны түсінікті.
Лемма. Сызықтық оператордың ядросы V  кеңістігінің ішкі кеңістігі болады.
кеңістігінің ішкі кеңістігі болады.
Дәлелдеу. Ішкі кеңістіктің критериі бойынша дәлелдейміз (қара, §2, теорема).
Айталық х,у  ker
ker 

 (х) = 0&
(х) = 0&  (у) = 0. х+у
(у) = 0. х+у  ker
ker  – ?
– ?
 (х + у) =
(х + у) =  (х) +
(х) +  (у) = 0+ 0=0
(у) = 0+ 0=0  х+у
х+у  ker
ker  .
.

 F,
F,  (
(  х) =
х) = 
 (х) =
(х) =  0= 0
0= 0 
 х
х  ker
ker  . Онда ker
. Онда ker  – ішкі кеңістік.
– ішкі кеңістік.
Анықтама.  сызықтық операторының ядросының өлшемі сызықтық оператордың дефектсі деп аталады. Белгілеуі def
сызықтық операторының ядросының өлшемі сызықтық оператордың дефектсі деп аталады. Белгілеуі def  . Сонда,
. Сонда,
def  = dim (ker
= dim (ker  ).
).
Дефект – ол сан. Ол сызықтық оператордың тек өзіне ғана байланысты, оның берілу әдісіне байланысты емес. Дефект – сызықтық оператордың инварианты.
Лемма. Сызықтық оператор нұқсансыз болуы үшін оның ядросы жалғыз нольдік вектордан тұруы қажет және жеткілікті. (Дәлелсіз).
Анықтама. V  кеңістігінің,
кеңістігінің,  сызықтық операторының нәтижесінде прообраздары бар векторларының жиынын
сызықтық операторының нәтижесінде прообраздары бар векторларының жиынын  сызықтық операторының образынемесе мәндерінің жиыныдеп атайды және im
сызықтық операторының образынемесе мәндерінің жиыныдеп атайды және im  деп белгілейді. (image – образ). Сонда,
деп белгілейді. (image – образ). Сонда,
im  =
= 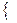 х
х  V
V  |
| 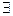 z
z  V
V 
 (z) = x
(z) = x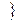 немесе
немесе
im  =
= 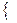
 (z) | z
(z) | z  V
V 
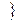 .
.
Анықтамадан im 
 V
V  болатыны түсінікті.
болатыны түсінікті.
Лемма. Сызықтық оператордың образы V  кеңістігінің ішкі кеңістігі болады.
кеңістігінің ішкі кеңістігі болады.
Дәлелдеу. Ішкі кеңістіктің критериі бойынша дәлелдейміз.
Айталық х,у  im
im 
 х=
х=  (z) & у =
(z) & у =  (t), z,t
(t), z,t  V
V  . x+y
. x+y  im
im  – ?
– ?
x + y =  (z) +
(z) +  (t) =
(t) =  (z +t)
(z +t)  х+у
х+у  im
im  .
.

 F,
F,  х =
х = 
 (z) =
(z) =  (
(  z)
z) 
 х
х  im
im  . Онда im
. Онда im  – ішкі кеңістік.
– ішкі кеңістік.
Анықтама.  сызықтық операторының образының өлшемі сызықтық оператордың рангсы деп аталады. Белгілеуі rang
сызықтық операторының образының өлшемі сызықтық оператордың рангсы деп аталады. Белгілеуі rang  . Сонда,
. Сонда,
rang  = dim (im
= dim (im  ).
).
Ранг – ол сан. Ранг да дефект тәрізді сызықтық оператордың берілу әдісіне байланысты емес, оның тек өзіне ғана байланысты. Ол да – сызықтық оператордың инварианты болады.
Лемма. Сызықтық оператордың рангсы оның матрицасының рангсына тең болады. (Дәлелсіз).
Сызықтық оператордың рангсы мен дефектсі бір-бірімен байланысты, атап айтқанда мына тұжырымдама дұрыс болады.
Теорема. Сызықтық оператор берілген векторлық кеңістіктің өлшемі сол оператордың дефектсі мен рангсының қосындысына тең болады:
dimV = def  + rang
+ rang 
немесе dimV = dim(ker  ) + dim(im
) + dim(im  ).
).
Теореманы дәлелсіз қабылдаймыз.
Ескерту. Соңғы теңдіктен V = ker  + im
+ im  теңдігі шықпайды.
теңдігі шықпайды.
Сызықтық оператордың меншікті векторлары мен
Меншікті мәндері
n  1. Матрицаның характеристикалық көпмүшелігі мен
1. Матрицаның характеристикалық көпмүшелігі мен
характеристикалық теңдеуі
Айталық, А –элементтері F өрісіне тиісті n-ші ретті квадрат матрица болсын:
А =  немесе қысқаша А = (
немесе қысқаша А = (  ), i,j=1,2,…,n.
), i,j=1,2,…,n.
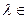 F делік. Берілген А матрицасымен қоса А–
F делік. Берілген А матрицасымен қоса А–  Е матрицасын қарастырамыз.
Е матрицасын қарастырамыз.
А–  Е =
Е =  .
.
Соңғы А–  Е матрицасының анықтауышы |А–
Е матрицасының анықтауышы |А–  Е| –
Е| –  -ға байланысты n-ші дәрежелі көпмүшелік болады:
-ға байланысты n-ші дәрежелі көпмүшелік болады:
|А–  Е| =
Е| =  = a
= a 
 +a
+a 
 +a
+a 
 +…+a
+…+a 
 +a
+a  .
.
Бұл көпмүшелікте  -нің коэффициенті a
-нің коэффициенті a  =(-1)
=(-1) 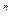 ,
,  -нің коэффициенті a
-нің коэффициенті a  А матрицасының бас диагоналы элементтерінің қосындысына (a
А матрицасының бас диагоналы элементтерінің қосындысына (a  =
=  +
+  + + ... +
+ + ... +  ), бос мүшесі a
), бос мүшесі a  А матрицасының анықтауышына тең болады (a
А матрицасының анықтауышына тең болады (a  =detА).
=detА).
Мысал. А=  ,
, 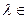 R. А–
R. А–  Е =
Е =  ;
;
|А–  Е| =
Е| =  = (жоғарыда айтқанымыздан, –
= (жоғарыда айтқанымыздан, –  +3
+3  +?
+?  +2 түріндегі көпмүшелік шығуы керек) = (1–
+2 түріндегі көпмүшелік шығуы керек) = (1–  )
) 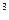 –(1–
–(1–  )+2(1–
)+2(1–  ) =1–3
) =1–3  +3
+3  –
–  –– 1+
–– 1+  +2–2
+2–2  = –
= –  +3
+3  –4
–4  +2.
+2.
Матрица 3-ші ретті болғанда,  -ның коэффициенті А матрицасының негізгі 3 анықтауышының қарама–қарсы таңбамен алынған қосындысына тең болады.
-ның коэффициенті А матрицасының негізгі 3 анықтауышының қарама–қарсы таңбамен алынған қосындысына тең болады.
Анықтама. |А–  Е| көпмүшелігін А матрицасының характеристикалық көпмүшелігі деп атайды. Оны
Е| көпмүшелігін А матрицасының характеристикалық көпмүшелігі деп атайды. Оны  (
(  ) деп белгілейміз.
) деп белгілейміз.
Анықтама.  (
(  ) = |А–
) = |А–  Е| = 0 теңдеуі А матрицасының характеристикалық теңдеуі деп, ал ол теңдеудің түбірлері А матрицасының характеристикалық сандары деп аталады.
Е| = 0 теңдеуі А матрицасының характеристикалық теңдеуі деп, ал ол теңдеудің түбірлері А матрицасының характеристикалық сандары деп аталады.
Ескерту. Алгебраның негізгі теоремасынан, характеристикалық теңдеудің С – комплекс сандар өрісінде ең болмағанда бір түбірі болатыны белгілі.
Айталық, Т – элементтері F өрісіне тиісті нұқсансыз n-ші ретті квадрат матрица болсын. Онда В = Т·А·Т  матрицасы А матрицасына ұқсас екенін білеміз. Осы В матрицасының характеристикалық көпмүшелігін есептейік.
матрицасы А матрицасына ұқсас екенін білеміз. Осы В матрицасының характеристикалық көпмүшелігін есептейік.
|В–  Е| = | Т·А·Т
Е| = | Т·А·Т  –
–  Е| = | Т·А·Т
Е| = | Т·А·Т  –
–  Т·Е·Т
Т·Е·Т  | = | Т·(А –
| = | Т·(А –  Е)·Т
Е)·Т  | =
| =
= |Т|·|А–  Е|·| Т
Е|·| Т  | = |Т||·| Т
| = |Т||·| Т  |·|А–
|·|А–  Е| = |А–
Е| = |А–  Е|.
Е|.
Сонда, ұқсас матрицалардың характеристикалық көпмүшеліктері тең.
Олай болса, барлық ұқсас матрицалардың характеристикалық көпмүшеліктері –  (
(  ) тең болады; онда
) тең болады; онда  (
(  ) = 0 – характеристикалық теңдеулері де және характеристикалық сандары да тең болады.
) = 0 – характеристикалық теңдеулері де және характеристикалық сандары да тең болады.
Егер А және В = Т·А·Т  ұқсас матрицаларын V
ұқсас матрицаларын V  кеңістігіндегі бір ғана
кеңістігіндегі бір ғана  сызықтық операторының әртүрлі базистегі матрицалары деп қарастырсақ, онда осы нәтижелерден төмендегідей қорытындыға келеміз:
сызықтық операторының әртүрлі базистегі матрицалары деп қарастырсақ, онда осы нәтижелерден төмендегідей қорытындыға келеміз:
Сызықтық оператордың матрицасының характеристикалық сандары базиске тәуелді емес.Сондықтан, оларды сызықтық оператордың характеристикалық сандары деп атайды.
Ескерту.  (
(  ) = |А
) = |А  –
–  Е| характеристикалық көпмүшелігін
Е| характеристикалық көпмүшелігін  сызықтық операторының характеристикалық көпмүшелігі деп, ал
сызықтық операторының характеристикалық көпмүшелігі деп, ал  (
(  ) = |А
) = |А  –
–  Е| = 0 характеристикалық теңдеуін
Е| = 0 характеристикалық теңдеуін  сызықтық операторының характеристикалық теңдеуі деп атайды.
сызықтық операторының характеристикалық теңдеуі деп атайды.
n  2. Сызықтық оператордың меншікті векторлары мен меншікті мәндері
2. Сызықтық оператордың меншікті векторлары мен меншікті мәндері
Айталық, 
 L(V
L(V  ),
), 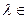 F болсын.
F болсын.
Анықтама. Егер нольдік емес а  V
V  векторы табылып,
векторы табылып,
 (а) =
(а) =  а
а
теңдігі орындалса, онда  скалярын
скалярын  сызықтық операторының меншікті мәні деп, ал а векторын
сызықтық операторының меншікті мәні деп, ал а векторын  сызықтық операторының,
сызықтық операторының,  меншікті мәніне сәйкес келетін, меншікті векторы деп атайды.
меншікті мәніне сәйкес келетін, меншікті векторы деп атайды.
Сонда, def
(  – меншікті мәні,
– меншікті мәні,  сыз.опер–ң )
сыз.опер–ң ) 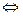 (
( 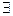 а
а 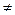 0
0  V
V 
 (а) =
(а) =  а ),
а ),
а –  –ға сәйкес келетін меншікті вектор.
–ға сәйкес келетін меншікті вектор.
Мысалдар.
1).  =
= 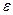 – бірлік оператор. Бұл сызықтық оператор үшін,
– бірлік оператор. Бұл сызықтық оператор үшін, 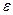 (а) = а = 1·а
(а) = а = 1·а
теңдігінен, меншікті мән 1 F, ал оған сәйкес меншікті вектор V
F, ал оған сәйкес меншікті вектор V  кеңісті –
кеңісті –
гінің кезкелген нольден өзге векторы болады.
2).  =
= 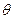 – нольдік оператор. Бұл сызықтық оператор үшін,
– нольдік оператор. Бұл сызықтық оператор үшін, 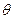 (а) = 0= 0·а
(а) = 0= 0·а
теңдігінен, меншікті мән 0 F, ал оған сәйкес меншікті вектор V
F, ал оған сәйкес меншікті вектор V  кеңісті –
кеңісті –
гінің кезкелген векторы болады.
3).  – жазықтықты
– жазықтықты 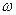 бұрышына бұру.
бұрышына бұру. 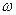 =0
=0  және
және 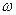 =
= 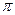 =180
=180  , жалпы,
, жалпы,
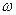 = к
= к 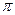 ,к
,к  Z жағдайларын алайық. Онда, сәйкесінше,
Z жағдайларын алайық. Онда, сәйкесінше, 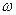 (а) = 0
(а) = 0  (а) = а = 1а;
(а) = а = 1а;
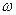 (а) =
(а) = 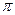 (а) = – а = ( –1) а болғандықтан
(а) = – а = ( –1) а болғандықтан  =1 және
=1 және  = –1 меншікті мәндер. Жалпы жағдайда,
= –1 меншікті мәндер. Жалпы жағдайда,  = ( – 1)
= ( – 1)  меншікті мәндер, ал кезкелген нольден өзге вектор меншікті вектор болады. Барлық басқа жағдайларда, яғни
меншікті мәндер, ал кезкелген нольден өзге вектор меншікті вектор болады. Барлық басқа жағдайларда, яғни  к
к 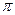
болғанда,  =
= 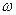 бұрышына бұру операторының меншікті векторлары болмайды.
бұрышына бұру операторының меншікті векторлары болмайды.
Ескерту. Бұл мысал, кезкелген сызықтық оператордың меншікті векторы бола бермейтінін көрсетеді.
n  3. Меншікті мәндер мен меншікті векторлардың қасиеттері
3. Меншікті мәндер мен меншікті векторлардың қасиеттері
1  . Әрбір меншікті вектор тек бір ғана меншікті мәнге сәйкес келеді.
. Әрбір меншікті вектор тек бір ғана меншікті мәнге сәйкес келеді.
Дәлелдеу. Кері жориық: а 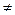 0векторы екі меншікті мәнге сәйкес келсін:
0векторы екі меншікті мәнге сәйкес келсін:
 (а) =
(а) = 
 а және
а және  (а) =
(а) = 
 а. Онда
а. Онда 
 а –
а – 
 а =
а =  (а) –
(а) –  (а) = 0
(а) = 0  |в.к.акс.|
|в.к.акс.|
 (
( 
 –
– 
 )а = 0
)а = 0  | а
| а 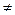 0 болғ., в.к.акс.|
0 болғ., в.к.акс.| 

 –
– 
 = 0
= 0 

 =
= 
 .
.
2  . Әрбір меншікті мәнге сәйкес келетін меншікті векторлар шексіз көп.
. Әрбір меншікті мәнге сәйкес келетін меншікті векторлар шексіз көп.
Олардың жиыны, нольдік векторды қоса есептегенде, векторлық кеңіс–
тіктің ішкі кеңістігін құрайды. Оны сол меншікті мәнге сәйкес келетін
меншікті ішкі кеңістік деп атайды.
W  =
= 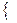 a
a  V
V  |
|  (а) =
(а) =  а
а 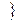 ;
;
W 

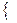 0
0 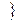 = W
= W 
 – ішкі кеңістік.
– ішкі кеңістік.
Дәлелдеу. Ішкі кеңістіктің критериі бойынша дәлелдейміз.
х, у  W
W 

 (х)=
(х)=  х,
х,  (у)=
(у)=  у және х
у және х 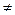 0, у
0, у 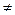 0. х + у
0. х + у  W
W 
 – ?
– ?
Егер х+у = 0 болса, онда х+у  W
W 
 .
.
Егер х+у 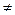 0 болса, онда
0 болса, онда  (х+у) =
(х+у) =  (х)+
(х)+  (у) =
(у) =  х+
х+  у =
у =  (х+у)
(х+у) 
 х+у
х+у  W
W  . Сондықтан х + у
. Сондықтан х + у  W
W 
 .
.


 F
F  х
х  W
W 
 – ?
– ?
 (
(  х) =
х) =  ·
·  (х) =
(х) =  ·
·  х =
х =  ·х =
·х =  ·х =
·х =  ·
·  х
х 
 х
х  W
W  . Онда
. Онда  х
х  W
W 
 .
.
Олай болса, W 
 – ішкі кеңістік.
– ішкі кеңістік.
3  . F өрісінде берілген V
. F өрісінде берілген V  векторлық кеңістіктегі
векторлық кеңістіктегі  сызықтық операторының
сызықтық операторының
меншікті мәндерінің жиыны сол оператордың характеристикалық теңдеуінің
F өрісіне тиісті болатын түбірлерінің жиынымен беттеседі.
Белгілеулер енгізейік.
L = 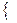
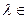 F |
F | 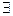 a
a 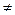 0
0  (а) =
(а) =  а
а 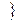 – меншікті мәндер жиыны,
– меншікті мәндер жиыны,
M = 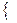
 F |
F |  (
(  ) º 0
) º 0 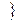 –
–  (
(  )=0 теңдеуінің түбірлерінің жиыны.
)=0 теңдеуінің түбірлерінің жиыны.
Сонда, L = М екенін дәлелдеу керек.
Ол үшін а) L  М , б) М
М , б) М  L болатынын көрсетеміз.
L болатынын көрсетеміз.
Дәлелдеу. V  векторлық кеңістігінің қандайда-бір е
векторлық кеңістігінің қандайда-бір е  , е
, е  , ... , е
, ... , е 
базисіндегі  сызықтық операторының матрицасы
сызықтық операторының матрицасы
А  =
=  болсын (
болсын ( 
 F).
F).
х =  е
е  + ... +
+ ... +  е
е  – кезкелген вектор, ал
– кезкелген вектор, ал  (х) =
(х) =  е
е  + ... +
+ ... +  е
е  – оның
– оның
образы делік. х пен  (х) векторларының координаталарының байланысы
(х) векторларының координаталарының байланысы
белгілі ( §4 қара): (  , ... ,
, ... ,  ) = (
) = (  , ... ,
, ... ,  ) А
) А  немесе
немесе
 =
= 
 +
+ 
 + … +
+ … + 

 =
= 
 +
+ 
 + … +
+ … + 
 (11; 1)
(11; 1)
………………………….
 =
= 
 +
+ 
 + … +
+ … + 

а) L  М – ? Айталық,
М – ? Айталық, 
 L болсын, яғни
L болсын, яғни 
 F – сызықтық оператордың
F – сызықтық оператордың
х меншікті векторы сәйкес келетін меншікті мәні болсын. Онда х 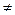 0 және
0 және
 (х) =
(х) =  х немесе (
х немесе (  , ... ,
, ... ,  ) = (
) = ( 
 , ... ,
, ... , 
 ) (11; 2)
) (11; 2)
(11; 2)-ні (11; 1)-ге қойып мынадай теңбе – теңдіктер жүйесін аламыз:
 (11; 3)
(11; 3)
(11; 3) жүйе –  , ... ,
, ... ,  скалярлары
скалярлары
 (11; 4)
(11; 4)
түріндегі біртекті СТЖ –ң нольден өзге шешулері екенін көрсетеді.
Нольден өзге шешулері болса, онда (11; 4) жүйенің анықтауышы нольге тең болғаны:
 º 0 (11; 5)
º 0 (11; 5)
Ал (11; 5) теңдік транспонирленген |А  –
– 
 Е| =
Е| =  (
( 
 ) º 0 теңдігі.
) º 0 теңдігі.
Онда 

 (
(  ) = |А
) = |А  –
–  Е| = 0 характеристикалық теңдеуінің түбірі, яғни
Е| = 0 характеристикалық теңдеуінің түбірі, яғни
ол характеристикалық сан (және ол F өрісіне тиісті). Онда 

 М. Олай
М. Олай
болса, L  М екені дәлелденді.
М екені дәлелденді.
б) М  L – ? Айталық
L – ? Айталық 
 М болсын, яғни
М болсын, яғни  –
–  сызықтық операторының
сызықтық операторының
F өрісіне тиісті болатын характеристикалық саны болсын. Ол
 (
( 
 ) = |А
) = |А  –
– 
 Е| º 0 деген сөз. Ал |А
Е| º 0 деген сөз. Ал |А  –
– 
 Е| анықтауышын транспонир-
Е| анықтауышын транспонир-
лесек те ол 0-ге тең болады, яғни (11; 5) теңдікті аламыз (тек 
 -ң орнына
-ң орнына

 тұрады). (11; 5) теңдік (11; 4) жүйенің анықтауышы. Біртекті СТЖ-ң
тұрады). (11; 5) теңдік (11; 4) жүйенің анықтауышы. Біртекті СТЖ-ң
анықтауышы нольге тең болғасын, оның нольдік емес шешулері болғаны.
Олардың біреуі (  ,
,  , ... ,
, ... ,  ) делік. Онда ол (11; 3), (11; 2) өрнектерге
) делік. Онда ол (11; 3), (11; 2) өрнектерге
ұқсас,  – ң орнына
– ң орнына  – ді қойғандағы өрнектерді қанағаттандырады.
– ді қойғандағы өрнектерді қанағаттандырады.
Онда координаталары (  ,
,  , ... ,
, ... ,  ) болатын х
) болатын х  векторы үшін
векторы үшін
 ( х
( х  ) =
) =  х
х 
теңдігі дұрыс болғаны. Онда  –
–  сызықтық операторының меншікті мәні,
сызықтық операторының меншікті мәні,
ал х  векторы оған сәйкес келетін меншікті вектор. Онда
векторы оған сәйкес келетін меншікті вектор. Онда 
 L. Олай болса,
L. Олай болса,
М  L екені дәлелденді.
L екені дәлелденді.
Дәлелденген а), б) жағдайлардан L = М. д.к.о.
(қара:  1
1  , 123 бет, теорема 5.8; қай дәлелдеу оңай, соны таңда).
, 123 бет, теорема 5.8; қай дәлелдеу оңай, соны таңда).
Дәлелденген қасиеттен төмендегідей практикалық ережеаламыз:
Алдымен, сызықтық оператордың барлық меншікті мәндерін табамыз. Олардың саны шекті (n – нен аспайды). Ол үшін характеристикалық теңдеудің түбірлерін табады. Ол түбірлердің тек негізгі өріске тиістілері ғана меншікті мәндер болады.
Сонан кейін, әрбір меншікті мәнге сәйкес келетін меншікті векторларды табамыз. Олар шексіз көп (олардың жиыны ішкі кеңістік құрайды). Сондықтан олардың тек сызықтық байланыссыз болатындарын (базис бола – тындарын) ғана табамыз. Ол үшін әрбір 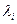 меншікті мәнін (11; 4) біртекті жүйеге
меншікті мәнін (11; 4) біртекті жүйеге  –ң орнына қояды да, оның базистік (фундаменталь) шешулерін табады. Сол базистік (фундаменталь) шешулер
–ң орнына қояды да, оның базистік (фундаменталь) шешулерін табады. Сол базистік (фундаменталь) шешулер 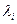 меншікті мәніне сәйкес келетін сызықтық байланыссыз меншікті векторлар болады (базис болады). Олардың саны бос айнымалылар санына, яғни n – r санына тең (мұндағы r – А
меншікті мәніне сәйкес келетін сызықтық байланыссыз меншікті векторлар болады (базис болады). Олардың саны бос айнымалылар санына, яғни n – r санына тең (мұндағы r – А  –
– 
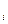 Ематрицасының рангсы).
Ематрицасының рангсы).
Мысал. Айталық V  – үш өлшемді декарттық R
– үш өлшемді декарттық R 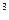 кеңістігі болсын (F = R).
кеңістігі болсын (F = R).
Осы кеңістікте  сызықтық операторы қандайда-бір базисте
сызықтық операторы қандайда-бір базисте
А  =
=  матрицасымен берілген. Осы оператордың меншікті мәндерін және әрбір меншікті мәнге сәйкес келетін меншікті векторларын табу керек:
матрицасымен берілген. Осы оператордың меншікті мәндерін және әрбір меншікті мәнге сәйкес келетін меншікті векторларын табу керек:  (х)=
(х)=  х,
х,  – ? х – ? х = (х
– ? х – ? х = (х  , х
, х  , х
, х 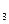 ).
).
Характеристикалық теңдеу құрамыз
|А  –
–  Е|=
Е|=  = –
= –  + 5
+ 5  – 8
– 8  +4 = – (
+4 = – (  – 5
– 5  + 8
+ 8  – 4) = 0.
– 4) = 0.
Түбірлерін табамыз. – 4-ң бөлгіштері:  ,
,  ,
,  . Ауызша, +1 түбірі екенін оңай есептейміз. Горнер схемасымен де есептеуге болады:
. Ауызша, +1 түбірі екенін оңай есептейміз. Горнер схемасымен де есептеуге болады:
| 1 | -5 | 8 |- 4
| 1 | 1 | -4 | 4 | 0 – (  – 1)(
– 1)(  – 4
– 4  + 4) = (
+ 4) = (  – 1)(
– 1)(  2)
2)  = 0.
= 0.
Сонда, түбірлері:  =
= 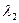 = 2
= 2  R –екі еселі түбір,
R –екі еселі түбір,  = 1
= 1  R –жай түбір.
R –жай түбір.
