Дербес туындылы дифференциалдық теңдеулерге келтірілетін негізгі есептер.

5.1.1-есеп.Біртекті материалдан жасалған қатты керілген ұзындығы 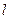-ге тең ішекті қарастырайық. Ішек тыныштық жағдайда ОХ осінің 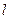кесіндісімен беттессін. Егер ішекті тартып, одан соң қоя берсек, онда ішек тербеліске ұшырайды. Ішек XOUжазықтығында (14-сурет) тербелсін және оның әрбір х нүктесі ОХ осіне перпендикуляр қозғалатын болсын (көлденең тербеліс). Ауырлық күшінің әсерін есепке алмаймыз.

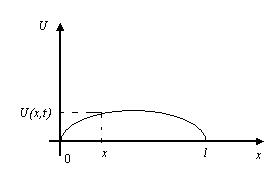
14-сурет

U –деп ішектің тыныштық жағдайдан х нүктесіндегі ауытқуын белгілейік. Бұл ауытқу уақытқа да байланысты болады. Демек, U-ауытқуы екі айнымалы функция, яғни U=U(x,t). Ішектің өте аз тербелісін қарастырған кезде, осы процеске сәйкес келетін математикалық модель

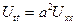
теңдеуі арқылы жазылатынын келесі пункте қарастырамыз. Бұл теңдеу бір өлшемді толқындық теңдеумен пара пар. Ішекке сыртқы күш әсер еткен кезде (мысалы, тартылыс күші) оған сәйкес келетін математикалық теңдеу

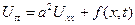
біртекті емес толқындық теңдеу арқылы жазылады. Бұл теңдеулердегі а –тұрақты физикалық шама, ал 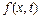сыртқы күшпен байланысты функция.

5.1.2-есеп. Біртекті материалдан жасалған қатты керіліп, ұштары бекітілген мембрананы қарастырайық. Мембрананың үстінен ұрып жіберсек, онда ол тербеліске ұшырайды. Мембрана тыныштық жағдайда ХОУ жазықтығының қандайда бір облысымен беттеседі (15-сурет) деп, ал тербеліс кезінде оның барлық Р(х,у) нүктелері осы жазықтыққа перпендикуляр қозғалады деп ұйғарайық. Ауырлық күшінің әсерін есепке алмаймыз. Сонымен бірге мембранаға сыртқы күш әсер етпейтін болсын.

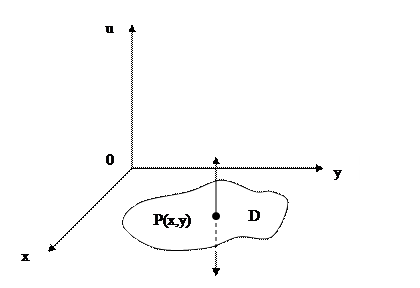
15-сурет

U –деп мембрананың t уақыт моментіндегі Р(х,у) нүктесіндегі тыныштық жағдайындағы ауытқуды белгілейік, яғни U=U(x,у,t). Онда мембрананың өте аз тербелісіне сәйкес келетін теңдеу

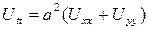
түрінде жазылады. Бұл теңдеу жазықтықта берілген толқындық теңдеуге пара - пар. Осы теңдеуге Лаплас операторын пайдаланып,

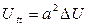
түрінде қайта жазуға болады. Мұндағы а- тұрақты физикалық шама.

5.1.3-есеп. Кеңістіктің қандай да бір нүктесінде дыбыс шығаратын құрал орналасқан болсын. Дыбыстың таралуына сәйкес келетін теңдеу кеңістікте берілген толқын теңдеуімен пара-пар.

Амплитудасы кішкентай механикалық тербелістерді физиктер толқындар деп атайды. Жоғарыда аталған теңдеулердің аттары осыған байланысты толқындық теңдеулер деп аталып кеткен. Физика курсында толқындар сфералық, цилиндрлік және жазық болып үшке бөлінеді. Осыған байланысты кеңістіктегі толқындық теңдеу сфералық толқындарға, жазықтықтағы толқындық теңдеу цилиндрлік толқындарға, ал бір өлшемді толқындық теңдеу жазық толқындарға сәйкес келеді.

(1.2.7), (1.2.8), (1.2.9) теңдеулеріне келтірілетін есептерді қарастырайық. Бұл теңдеулер жылу таралу процесімен байланысты болғандықтан, оларды жылуөткізгіштік теңдеулері деп атайды.

5.1.4-есеп. Ұзындығы 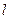-ге тең біртекті жұқа материалдан жасалған стерженьді қарастырайық. Бастапқы жағдайда ол бірқалыпты қыздырылмаған болсын деп ұйғарайық. Онда оның жылу өткізгіштігіне байланысты көбірек қызған бөлігінен азырақ қызған бөлігіне қарай жылу беру процесі пайда болады. Сондықтан стерженьнің әрбір нүктесіндегі 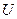температурасы нүктесіне және 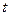уақытқа байланысты екі айнымалы U=U(x,t) функциясын анықтайды. Егер стерженьнің бүйір беті мен шеті жылу өткізбейтін, яғни сыртқы ортамен жылу алмасу процесі болмаса, және қосымша стерженьнің ішінде жылу көзі жоқ болса, онда стерженьнің кез келген нүктесіндегі температура біраз уақыт өткеннен кейін теңесіп, стерженьнің бойында тұрақты температура пайда болады. Стерженьнің бүйір беті жылу өткізбейді және ішкі жылу көзі болмаған жағдайда U=U(x,t) температурасы

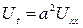
біртекті теңдеуді қанағаттандырады. Егер ішкі жылу көзі болса, онда жылуөткізгіштік теңдеуі

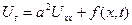
біртекті емес теңдеу түрінде анықталады. Егер стерженьнің бүйір беті арқылы сыртқы ортамен жылу алмасу процесі болатын болса, онда жылуөткізгіштік теңдеуі күрделі

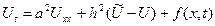
түріндегі теңдеу арқылы беріледі. Мұндағы 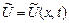сыртқы ортадағы температура, 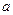-жылу өткізгіш коэффиценті, ал 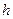-жылу алмасу коэффиценті. Олар стерженьнің жасалған материалына байланысты болады.

5.1.5-есеп. Кеңістікте қалыпты қыздырылмаған біртекті қатты дене берілсін. Әлбетте, оның жылу өткізгіштігіне байланысты көбірек қызған бөлігінен азырақ қызған бөлігіне қарай жылу алмасу процесі пайда болады. Нәтижесінде уақыт өткен сайын дененің әрбір нүктесінің температурасы өзгеріп отырады. Сондықтан дененің әр нүктесіндегі 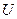температурасы 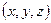нүктесіне және 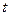уақытқа байланысты 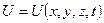функциясы арқылы анықталады. Дененің ішінде жылу көзі болмаған жағдайда 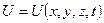функциясы

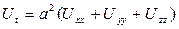
теңдеуін қанағаттандырады. Егер дененің ішінде қосымша жылу көзі бар болса, онда жылуөткізгіштік теңдеуі

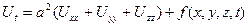
біртекті емес теңдеу түрінде анықталады. Бұл теңдеуді Лаплас операторының анықтамасын пайдаланып,

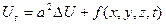
түрінде жаза аламыз. Әлбетте, бір және екі өлшемді жылуөткізгіштік теңдеулері кеңістіктегі жылуөткізгіштік теңдеуінің дербес жағдайы болып табылады.

Жоғарыда біз уақытқа және кеңістіктегі орнына байланысты өзгеріп отыратын процесті қарастырдық. Бірақ, уақытқа байланыссыз, тек орнына байланысты өзгеріп отыратын процестер де жиі кездеседі. Мұндай процестерді стационар процестер деп атайды. Көптеген процестер біршама уақыттан кейін стационар процеске айналады. Мысалы, денедегі температураның таралуы көп уақыт өткеннен кейін уақытқа байланысты болмайды. Демек, 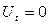. Сондықтан температураның стационар таралуын сипаттайтын теңдеу 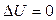түрінде анықталады. Бұл - Лаплас теңдеуі. Егер дененің ішінде уақытқа байланыссыз өзеретін жылу көзі болса, онда стационарлық процесс

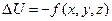
Пуассон теңдеуі арқылы сипатталады.

5.1.1 - ескерту. Лаплас және Пуассон теңдеулеріне стационарлық процестерден де басқа, физика облысында (электростатикада, гидродинамикада) және техникада (мысалы, пайдалы қазбаларды электрлік әдістер арқылы іздестіру) кездесетін көптеген есептер келеді. Бірақ, көрсетілген теңдеулерді зерттеген кезде U функциясын температураның функциясы ретінде қарастырған өте ыңғайлы. Дәл осы сияқты жылуөткізгіштік теңдеуі жылудың таралу процесімен қатар диффузиялық процестерді (мысалы, түтін шығатын трубадағы түтін диффузиясы) сипаттайды. Толқындық теңдеулер электромагниттік өрістерді, электрлік толқындарды зерттегенде гидродинамика және акустикада, серпімділік теориясында кездесетін есептерді шығару кезінде пайда болады. Ілгеріде, біз математикалық физика теңдеулері қолданылатын облыстардың барлығын бұл курста қарастыра алмайтын болғандықтан, өте қарапайым модельге сәйкес келетін процестердің теңдеулерін қорытып шығарамыз.

5.2. Ішектің тербеліс теңдеуін қорытып шығару.Ішек тербеліс теңдеуінің математикалық моделін құру үшін ішектің 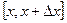бөлігіне әсер ететін барлық күштерді қарастырамыз (16-сурет). Ішек июге ешқандай кедергі жасамағандықтан оған әсер ететін керілу күші ішектің 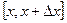бөлігінің шеткі нүктелері арқылы жүргізілген жанама бойымен бағытталады. Ішектің өте кіші тербелісін қарастырғандықтан, 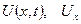шамалары өте кішкентай болады. Сондықтан, олардың көбейтінділерін және квадраттарын ескермеуімізге болады. Енді ішектің 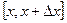аралығындағы бөлігін қарастырамыз. Ауытқу кезінде 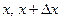нүктелері сәйкесінше М₁, М₂ нүктелеріне көшеді. Ішектің кез келген 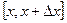бөлігі ауытқу кезінде өзінің ұзындығын өзгертпейді. Шынында, да

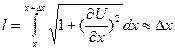
Сондықтан Гук заңы бойынша керілу күшінің шамасы 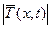және 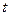аргументтерінің барлық мәндерінде тұрақты болады, яғни 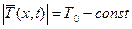. 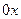өсіне перпендикуляр бағытталатын 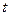уақыт кезіндегі нүктесіне әсер ететін сыртқы күштің тығыздығын 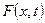деп белгілейік. Енді ішектің қарастырып отырған бөлігіне Ньютонның ІІ заңын пайдалансақ, онда 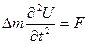немесе 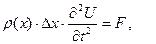мұндағы 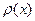-ішектің х нүктесіндегі тығыздығы, 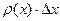ішектің 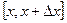кесіндісіндегі массасы, ал 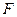осы нүктеге әсер ететін күш. 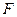күші тербеліс көлденең болғандықтан ішектің 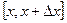бөлігінің ұштарына әсер етуші керілу күштердің вертикаль проекцияларынан және сырттай әсер ететін

күштің қосындыларынан тұрады.

16-сурет

Олай болса,

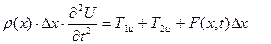
немесе

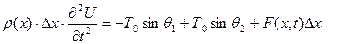(5.2.1)

Кішкентай ауытқулар үшін 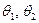өте аз шама болғандықтан,

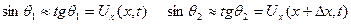
ескеріп, (5.2.1) теңдігінен

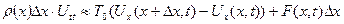
жуық теңдігіне келеміз. Дәл теңдік алу үшін жоғарыдағы жуық теңдіктің екі жағын 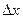–ке бөліп, оны нөлге ұмтылдырамыз, яғни

.

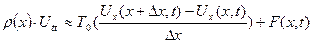Бұдан

,

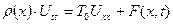өйткені

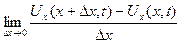
бар және ол 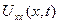-ке тең.

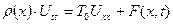
теңдеуін еркін емес ішек тербелісінің теңдеуі деп атайды.

Егер ішектің тығыздығы барлық жерде бірдей болса, 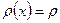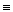const , яғни ішек біртекті материалдан жасалған болса, онда ішектің тербеліс теңдеуі

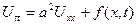(5.2.2)

түрінде жазылады, мұндағы 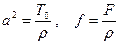. (5.2.2) теңдеуін бір өлшемді толқындық теңдеуі деп те атайды.

Жоғарыда қорытып шығарған сияқты мембрананың кішкентай көлденең тербелісінің теңдеуі

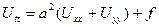
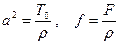(5.2.3)

түрінде болатындығын көрсетуге болады. (5.2.3) теңдеуін екі өлшемді толқындық теңдеу деп те атайды.

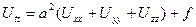(5.2.4)

үш өлшемді толқындық теңдеуі біртекті ортада таралатын дыбыстың таралу процесіне сәйкес келетін теңдеу.

Біз (5.2.2), (5.2.3) және (5.2.4) теңдеулерін Лаплас операторын пайдаланып, бір формула

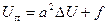
түрінде жазатын боламыз.

5.3. Жылуөткізгіштік теңдеуін қорытып шығару.Ұзындығы 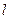-ге тең болатын қандай да бір материалдан жасалған стержень берілсін. (17-сурет).

17-сурет

Стерженьнің кішкентай 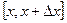бөлігіндегі температурасының өзгеру заңдылығын өрнектейтін теңдеуді құру керек. Стерженьнің бойымен таралатын жылудың математикалық моделін жасау үшін төмендегі көрсетілген ұйғарымды жасайық: стержень жылу өткізетін біртекті материалдан жасалған; стерженьнің бүйір беттері жылу өткізбейді, яғни жылу 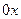өсімен ғана таралуы мүмкін; стержень өте жұқа, яғни стерженьнің кез келген көлденең қимасындағы температура барлық жерде бірдей.

Стерженьнің 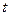уақыт моментіндегі нүктесіндегі температурасын U(x,t) деп, ал 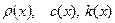деп нүктесіндегі сәйкесінше оның тығыздығын, меншікті жылу сыйымдылығын және жылу өткізгіш коэффициентін белгілейік. 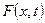- 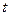уақыт моментіндегі стерженьнің нүктесінде орналасқан жылу көзінің тығыздығы болсын. Физикадан белгілі жылу мөлшерінің сақталу заңын: «Стерженьнің S қимасындағы жылу мөлшері осы қиманың шекарасы арқылы өтетін толық жылу мөлшеріне, стерженьнің ішкі жылу көзі арқылы пайда болатын толық жылу мөлшерін қосқанға тең» деген тұжырымды пайдаланып, осы стерженьнің S қимасындағы 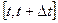уақыт кезіндегі балансын есептейік. Фурье заңы бойынша, стерженьнің 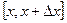бөлігіндегі температураны 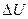-ға көтеру үшін кететін жылу мөлшері

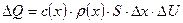
формуласы арқылы есептеледі. Мұндағы с(х) стерженьнің нүктесіндегі жылу сыйымдылығы (массасы 1кг тең дененің температурасын 1⁰ –қа көтеруге кететін жылу мөлшері). Стерженьнің сол жақ ұшынан 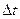уақыт кезінде ағып өтетін жылу мөлшері

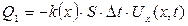
формуласымен есептеледі, мұндағы 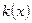стерженьнің жылу өткізгіштік коэффиценті(қарама-қарсы шеттеріндегі температураның айырымы 1^о тең болған кезде ұзындығы және көлденең қимасының ауданы 1-ге тең стерженьнен 1 секундта өтетін жылу мөлшеріне тең шама). Бұл формуладағы минус таңбасы ерекше түсіндіруді қажет етеді. Әдетте, ағым 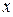-тің өсу бағытына қарай ағатын болса,оң бағытталған деп есептеледі. Бұл жағдайда нүктесінің сол жағындағы температураның мәні оң жағынан үлкен болады. Демек, 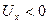болу керек. Сондықтан Q₁-дің мәні оң болу үшін формуланың алдына минус таңбасы қойылады. Дәл осы сияқты стерженьнің оң ұшынан 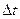уақыт кезінде ағып өтетін жылу мөлшері

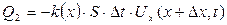
формуламен есептелінеді. Егер стерженьнің тығыздығы 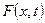–ға тең ( уақыт бірлігіндегі бірлік бөліктен шығатын жылу шамасы) болатын жылу көзі болса, онда жылу мөлшерінің сақталу заңын пайдаланып,

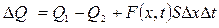
немесе

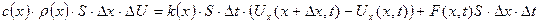(5.3.1)

теңдігін аламыз. Осы теңдікті 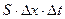өрнегіне бөліп, 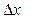пен 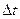-ны нөлге ұмтылдырсақ, онда (5.3.1) теңдігінен

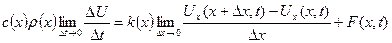
түріндегі теңдікке келеміз. Соңғы теңдіктен

,

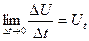ал

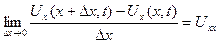
екенін ескеріп,

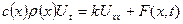(5.3.2)

теңдігін аламыз.

Егер стержень біртекті болса, онда с, 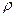және 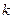шамалары тұрақты болады. Бұл жағдайда (5.3.2) теңдігін

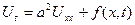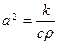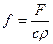, , (5.3.3)

түрінде жазуға болады. (5.3.3) теңдеуін бір өлшемді жылуөткізгіштік теңдеуі деп атайды.

Дәл жоғарыда көрсетілген әдісті пайдаланып, егер дене өте жұқа пластинка болса, онда

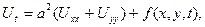(5.3.4)

ал дене үш өлшемді кеңістікте берілген біртекті қатты изотропты дене болса, онда

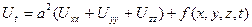(5.3.5)

теңдіктері сәйкесінше денедегі температураның өзгеру заңдылығын сипаттайтын теңдеулерді анықтайтындығын қорытып шығаруға болады.

(5.3.4) теңдеуін екі өлшемді, ал (5.3.5) теңдеуін үш өлшемді жылуөткізгіштік теңдеулері деп атайды. Оларды Лаплас операторын пайдаланып,

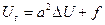
бір формула түрінде жазуға болады.

5.4. Стационар теңдеу. Стационарлық процестер үшін 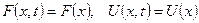болғандықтан, толқындық та, жылуөткізгіштік теңдеулері де

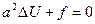
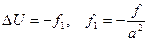(5.4.1)

түрінде беріледі. (5.4.1) теңдеуін Пуассон теңдеуі деп атайды. Егер (5.4.1) теңдеуіндегі 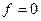болса, яғни 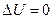, онда оны Лаплас теңдеуі деп атайды.