Определенный интеграл как функция верхнего предела

Если функция f(x) интегрируема на отрезке [a,b], то она интегрируема и на отрезке [a,x], где . Рассмотрим функцию аргумента x

.

(7.10.1)

Назовем функцию F(x) интегралом с переменным верхним пределом. В формуле (7.10.1) переменная интегрирования обозначена буквой t , чтобы избежать путаницы с переменным верхним пределом x.

Теорема

Непрерывная на отрезке [a,b] функция f(x) имеет на этом отрезке первообразную. Одной из первообразных является функция .

Таким образом, любая непрерывная на отрезке [a,b] функция f(x) имеет на этом отрезке первообразную в форме определенного интеграла F(x) с переменным верхним пределом. Поскольку всякая другая первообразная отличается от F(x) на постоянную величину, то связь между неопределенным и определенным интегралами имеет вид , где С – произвольная постоянная.

7.12. Формула Ньютона–Лейбница

Согласно Теореме (см. раздел 7.10), непрерывная на отрезке [a,b] функция f(x) имеет на этом отрезке первообразную, которая определяется формулой

,

(7.12.1)

где С – произвольная постоянная. Подставляя x=a в формулу (7.12.1), получаем с учетом свойства (1) определенного интеграла: откуда C= -F(a).

Тогда из выражения (7.12.1) имеем.

Полагая теперьx x=b, получаем формулу

(7.12.2)

Равенство (7.12.2) называется основной формулой интегрального исчисления, или формулой Ньютона–Лейбница.

Разность F(b) - F(a) условно записывают символом . Формула (7.12.2) дает широкие возможности для вычисления определенных интегралов.

Замена переменной и формула интегрирования по частям в определенном интеграле

Теорема

Пусть:

1) f(x) – непрерывная функция на отрезке ;

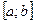2) функция дифференцируема на , а непрерывна на ;

3) .

Тогда справедлива формула

(7.13.1)

Формула (7.13.1) называется формулой замены переменной или подстановки в определенном интеграле.

Заметим, что при вычислении определенного интеграла с помощью замены переменной нет нужды возвращаться к прежней переменной, как при вычислении неопределенного интеграла, так как определенный интеграл представляет собой число, которое, согласно формуле (7.13.1) равно значению каждого из рассматриваемых интегралов. Теперь при подстановке следует сначала найти новые пределы интегрирования и выполнить необходимые преобразования подынтегральной функции.

Пример

1. .

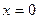Выполним подстановку.t=1+ Тогда, dt=2x dx t=1 при и t=2 при.x=1.

.

2. .

Выполним подстановку x = a sin t.

Тогда, dx = a cos t dt, , при x = 0, при x = a. Подставляя все в исходный интеграл, получим

.

Теорема: Пусть функции u(x) и v(x) имеют непрерывные производные на отрезке 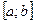. Тогда справедлива формула

(7.13.2)

Равенство (7.13.2) называется формулой интегрирования по частям в определенном интеграле.

Пример

1. .

Положим здесь , . Получаем

.

2. .

Здесь , . Далее по формуле (7.13.2):

.