Магнитная постоянная. Единицы магнитной индукции и напряженности магнитного поля

Если два параллельных проводника с то-ком находятся в вакууме (m=1) то сила взаи-модействия на единицу длины проводника, согласно (15.13), равна

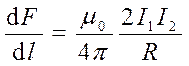. (15.14)

Для нахождения числового значения магнитной постоянной m₀воспользуемся определением ампера, согласно которому 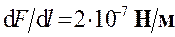при I₁=I₂=1 А и R=1 м. Подставив это значение в фор­мулу (15.14), получим

,

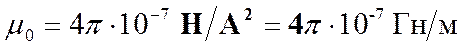где генри (Гн) — единица индуктивности.

Закон Ампера позволяет определить единицу магнитной индукции В. Предполо­жим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда из закон Ампера (dF=IBdl)

.

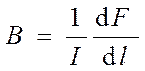Единица магнитной индукции — тесла (Тл): 1 Тл - магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н на каждый метр длины прямолинейного проводника, расположённого перпендикулярно направлению поля, если по этому проводнику проходит ток 1 А:

1 Тл=1 Н/(А∙м).

Так как m₀=4p∙10^-7 Н/А², а в случае вакуума (m=1), В=m₀ Н, то для данного случая

Н=В/m₀.

Единица напряженности магнитного поля -ампер на метр (А/м):1 А/м - напря­женность такого поля, магнитная индукция которого в вакууме равна 4p∙10^-7 Тл.

Действие магнитного поля на

Движущийся заряд

Магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой

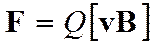, (15.17)

где В -индукция магнитного поля, в котором заряд движется.

Направление силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q>0 направления I и v совпадают, для Q<0 - противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис.15.9 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точка-ми) и F для положи­тельного заряда. На отрицательный заряд сила действует в противоположном направ­лении. Модуль силы Лоренца (см. (15.17)) равен

,

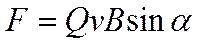где a - угол между v и В.

Отметим еще раз, что магнитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрического. Магнитное поле действует только на движущиеся в нем заряды.

Так как по действию силы Лоренца можно найти модуль и направление вектора В, то выражение для силы Лоренца может быть использовано для определения вектора магнитной индукции В.

Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянно магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.

Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца:

.

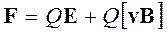Это выражение называется формулой Лоренца. Скорость v в этой формуле есть ско­рость заряда относительно магнитного поля.