Скінченні кільця і скінченні поля

Лекція № 7

Тема: Скінченні поля

План лекції:

1. Скінченні кільця і скінченні поля.

2. Скінченні поля на базі кілець класів лишків 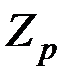за даним простим модулем.

3. Характеристика поля.

4. Число елементів скінченного поля.

5. Примітивні елементи скінченного поля.

Скінченні кільця і скінченні поля

Згадаємо, що кільцем 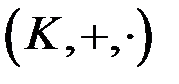називається непорожня множина 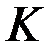, на якій визначені дві бінарні алгебраїчні операція + (додавання) і 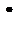(множення), такі, що

1. 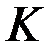– абелева група відносно операції + (адитивна група кільця).

2. 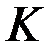– півгрупа відносно операції 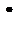(мультиплікативна півгрупа кільця).

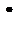3. Операція (множення) дистрибутивна зліва і справа відносно операції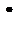+(додавання): ; .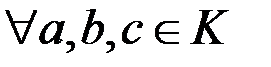

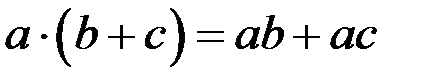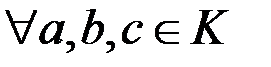
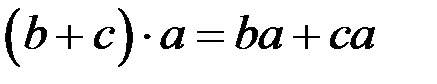Операції + і 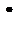не обов’язково є звичайними операціями додавання і множення. Нейтральний елемент адитивної групи кільця називається нулем кільця і позначається 0, а симетричний елемент позначається .

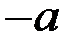Найпростішій приклад кільця – кільце цілих чисел .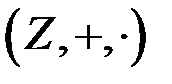

Існують наступні класи кілець:

Кільце 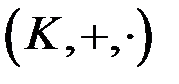називається кільцем з одиницею, якщо в 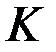існує одиничний елемент 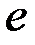, відмінний від нульового, тобто 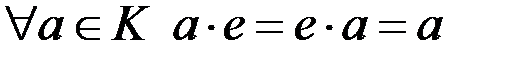. Далі одиницю будемо позначати як 1.

Кільце 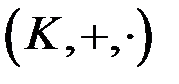називається комутативним, якщо операція 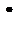є комутативною, тобто .

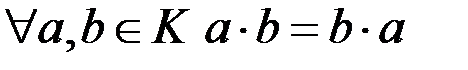Кільце 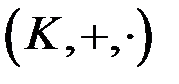називається цілісним (або областю цілісності), якщо воно є комутативним кільцем з одиницею, в якому з рівності 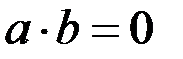випливає 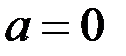або 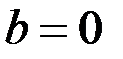. Оскільки ненульові елементи з властивістю 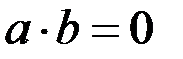називають дільниками нуля, то цілісне кільце ще називають кільцем без дільників нуля.

Кільце цілих чисел 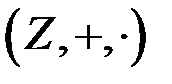є цілісне кільце.

Кільце 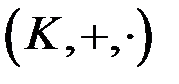називається тілом, якщо 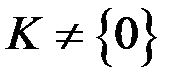і всі ненульові елементи в 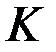утворюють групу відносно операції .

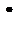Оскільки основною алгебраїчною структурою, яка буде використовуватися надалі, є поле, особливу увагу звернемо на його означення.

Полем 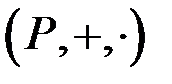називається множина 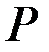на якій визначені дві бінарні алгебраїчні операція + (додавання) і 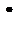(множення) такі, що

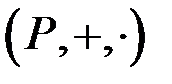1. – комутативне кільце з одиницею;2. Для кожного ненульового елемента 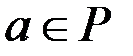існує в 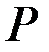обернений до нього елемент : .

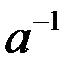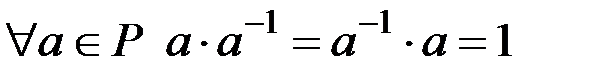Отже, поле – це комутативне кільце з одиницею, в якому кожний елемент має обернений.

Поле 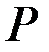являє собою поєднання на одній і тій самій множині двох абелевих груп – адитивної групи 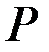і мультиплікативної 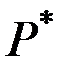, зв'язаних дистрибутивним законом (тепер вже одним, з-за комутативності).

Поле можна визначити ще як комутативне тіло.

Зокрема, поле є цілісним кільцем. Обернене твердження вірне лише у випадку скінченного кільця.

Теорема. Кожне скінченне цілісне кільце є полем.

Означення. Непорожня підмножина 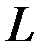кільця 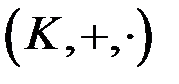називається підкільцем цього кільця, якщо 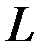замкнене відносно алгебраїчних операцій + і 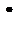і утворює кільце відносно цих операцій.

Означення. Непорожня підмножина 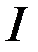кільця 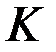називається ідеалом кільця 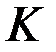, якщо 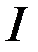є підкільцем кільця 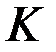і для будь-який елементів 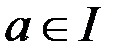і , .

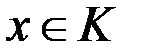
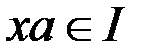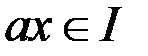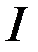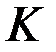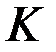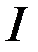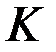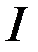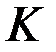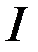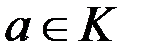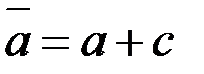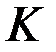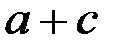Оскільки ідеали є нормальними (ліві суміжні класи співпадають з правими) підгрупами адитивної групи кільця, то кожен ідеал кільця визначає деяке раз биття множини на суміжні класи за адитивною підгрупою , які називаються класами лишків кільця за модулем ідеалу . Клас лишків кільця за модулем ідеалу , що містить елемент , позначають через , оскільки він складається з усіх елементів виду , де 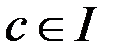. Елементи 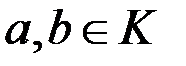, які належать одному і тому ж класу лишків за модулем ідеалу 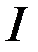(тобто такі, що 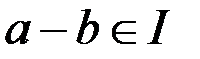), називають конгруентними за модулем ідеалу 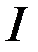і позначають 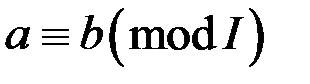. Для них справедливо:

1. Якщ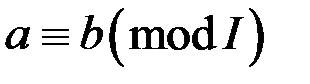о , то , , , , .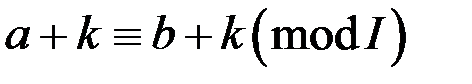

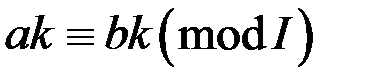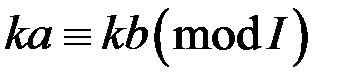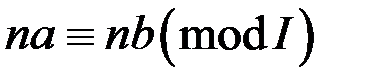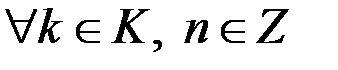2. Якщ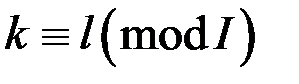о , то , .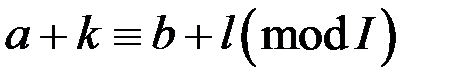

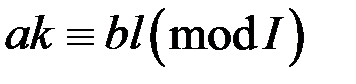Теорема (про факторкільце). Множина всіх класів лишків кільця 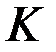за модулем ідеалу 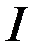відносно операцій додавання і множення, визначених наступним чином:

;

,

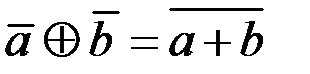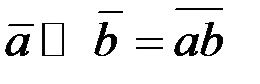є кільцем. Це кільце називаєтьсяфакторкільцемкільця 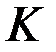за модулем ідеалу 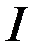і позначається .

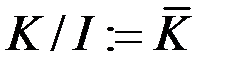Приклад 1. Якщо 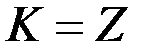, , 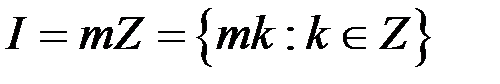то кільце класів лишків цілих чисел 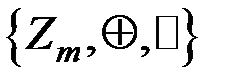, де 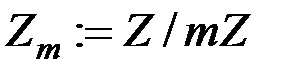є прикладом скінченного кільця і має широкі застосування в теорії чисел. Елементами кільця 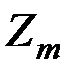є 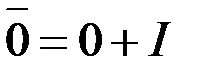, , 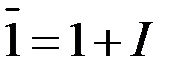, 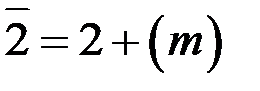…, 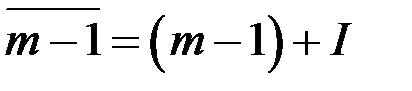. В кільці класів лишків звичайно оперують з фіксованою множиною представників за модулем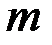 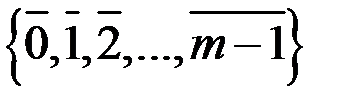. У позначеннях також відмовляються від рисочок і кружечків.

В окремому випадку 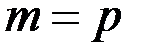, де 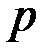– просте число скінченне кільце лишків 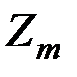стає полем.

Теорема (про факторкільце 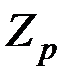). Факторкільце 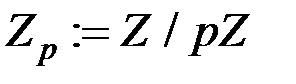кільця цілих чисел за ідеалом, породженим простим числом 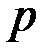, є полем.

Приклад 2. Нехай 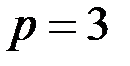. Тоді кільце 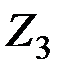складається з трьох елементів 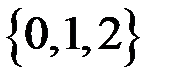, операції в кільці можна задати таблицями Келі:

+

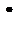Останній приклад є першим зразком скінченного поля, тобто поля, множина елементів якого скінченна. Ці поля відіграють основну роль в сучасній криптографії.